4.4. Ряд Тейлора (Маклорена).

  ЗАДАНИЕ N 30 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Ряд Маклорена для функции   имеет вид …

Решение: Так как ряд Маклорена для функции   имеет вид    то при 

  ЗАДАНИЕ N 29 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Ряд Маклорена для функции   имеет вид …

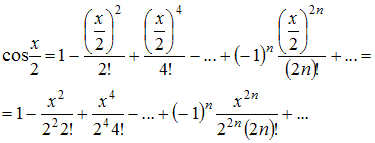Решение: Так как ряд Маклорена для функции   имеет вид    то  при 

  ЗАДАНИЕ N 31 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Ряд Маклорена для функции   имеет вид …

Решение: Так как ряд Маклорена для функции   имеет вид    то  при 

  ЗАДАНИЕ N 16 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Если   то коэффициент a₃ разложения данной функции в ряд Тейлора по степеням   равен …

			9
			– 1
			1
			18

Решение: Так как коэффициенты данного ряда Тейлора вычисляются по формул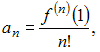е   то вычислим последовательно производные:     Тогда 

  ЗАДАНИЕ N 37 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Если 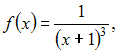  то коэффициент a₃ разложения данной функции в ряд Маклорена равен …

			– 10
			10
			6
			– 6

Решение: Так как разложение в ряд Маклорена функции   имеет вид:  то   или, учитывая, что   получаем 

  ЗАДАНИЕ N 19 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Если   то первые три (отличные от нуля) члена разложения этой функции в ряд Маклорена имеют вид …

Решение: Из разложения в ряд Маклорена функции   следует,  что

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Разложение в ряд Тейлора функции   в окрестности точки   имеет вид …

Решение: Так как коэффициенты данного ряда Тейлора вычисляются по формуле   то вычислим последовательно:        … Тогда 

 ЗАДАНИЕ N 7 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Если  , то первые три (отличные от нуля) члена разложения этой функции в ряд Маклорена  имеют вид …

 ЗАДАНИЕ N 27 сообщить об ошибке Тема: Ряд Тейлора (Маклорена) Если   то первые три (отличные от нуля) члена разложения этой функции в ряд Маклорена имеют вид …

ДЕ 5. Дифференциальные уравнения

5.1. Типы дифференциальных уравнений

5.2. Однородные дифференциальные уравнения

5.3. Задача Коши для дифференциального уравнения первого порядка

5.4. Дифференциальные уравнения высших порядков, допускающие понижение порядка