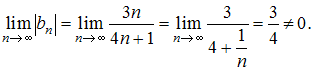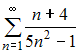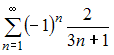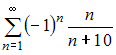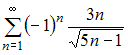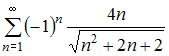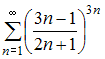4.2. Сходимость числовых рядов.

  ЗАДАНИЕ N 32 сообщить об ошибке Тема: Сходимость числовых рядов Сумма числового ряда 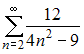  равна …

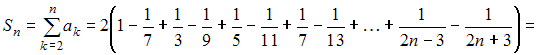
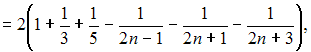
Решение: Представим общий член этого ряда в виде суммы простейших дробей:  и вычислим n – ую частичную сумму ряда:   Тогда 

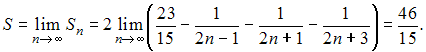
  ЗАДАНИЕ N 20 сообщить об ошибке Тема: Сходимость числовых рядов Числовой ряд 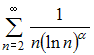  сходится при  , равном …

			2
			1
			0,5
			0

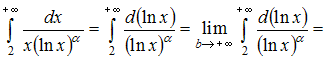
Решение: Применим интегральный признак сходимости Коши, то есть исследуем  на сходимость несобственный интеграл: 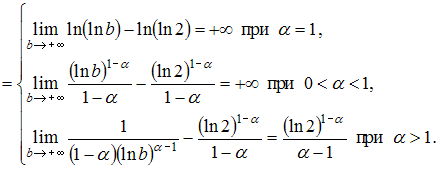Таким образом, данный ряд сходится при   например, при 

  ЗАДАНИЕ N 28 сообщить об ошибке Тема: Сходимость числовых рядов Сходящимся является числовой ряд …

Решение: Из представленных числовых рядов сходящимся является ряд 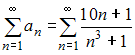  Действительно, так как при применении теоремы сравнения со сходящимся обобщенным гармоническим рядом 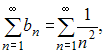  получаем: 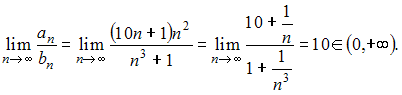  А это означает, что ряд   сходится. Для рядов   и   не выполняется необходимое условие сходимости, а расходимость ряда   устанавливается сравнением с гармоническим рядом.

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Сходимость числовых рядов Сходящимся является числовой ряд …

Решение: Из представленных числовых рядов сходящимся является ряд 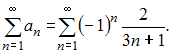  Действительно, при применении признака сходимости Лейбница, получаем: 1)   2) для любого натурального   справедливо 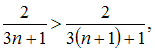   то есть последовательность   монотонно убывает. Следовательно, ряд   сходится. Для остальных рядов 

  ЗАДАНИЕ N 13 сообщить об ошибке Тема: Сходимость числовых рядов Сходящимся является числовой ряд …

Решение: Из представленных числовых рядов сходящимся является ряд 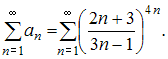  Действительно, так как при применении радикального признака Коши, получаем: 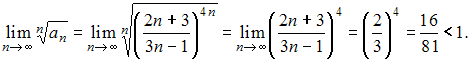  Для остальных рядов аналогичный предел будет принимать значения, большие единицы.

  ЗАДАНИЕ N 29 сообщить об ошибке Тема: Сходимость числовых рядов Даны числовые ряды: А) 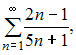 В) 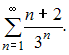 Тогда …

			ряд А) расходится, ряд В) сходится
			ряд А) расходится, ряд В) расходится
			ряд А) сходится, ряд В) сходится
			ряд А) сходится, ряд В) расходится

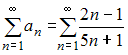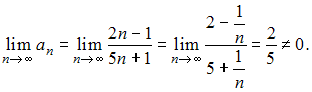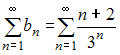Решение: Ряд   расходится, так как для него не выполняется необходимое условие сходимости. Действительно,  Для исследования сходимости ряда   применим признак сходимости Даламбера. Тогда 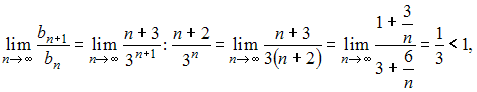   то есть ряд сходится.

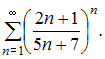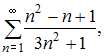  ЗАДАНИЕ N 29 сообщить об ошибке Тема: Сходимость числовых рядов Даны числовые ряды: А)  В)  Тогда …

			ряд А) сходится, ряд В) расходится
			ряд А) расходится, ряд В) расходится
			ряд А) сходится, ряд В) сходится
			ряд А) расходится, ряд В) сходится

Решение: Для исследования сходимости ря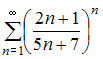да   применим радикальный признак сходимости Коши. Тогда 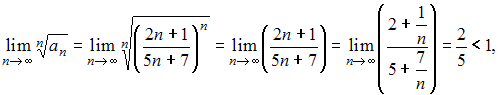 то есть ряд сходится. Ряд   расходится, так как для него не выполняется необходимое условие сходимости. Действительно,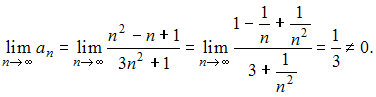 

  ЗАДАНИЕ N 35 сообщить об ошибке Тема: Сходимость числовых рядов Даны числовые ряды: А) 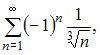 В)  Тогда …

			ряд А) сходится, ряд В) расходится
			ряд А) расходится, ряд В) расходится
			ряд А) сходится, ряд В) сходится
			ряд А) расходится, ряд В) сходится

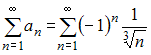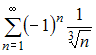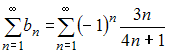Решение: Для исследования сходимости знакочередующегося ряда   применим признак сходимости Лейбница.  Тогда: 1) вычислим предел  2) для любого натурального   справедливо    то есть последовательность   монотонно убывает. Следовательно, ряд   сходится. Ряд   расходится, так как