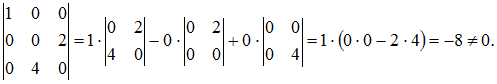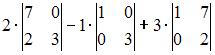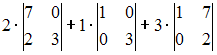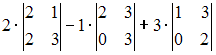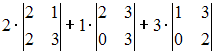- •Структура теста
- •1.1. Вычисление определителей.
- •1.2. Умножение матриц.
- •1.3. Определение линейного пространства.
- •1.4. Квадратичные формы.
- •2.1. Полярные координаты на плоскости.
- •2.2. Прямая на плоскости.
- •2.3. Кривые второго порядка.
- •2.4. Плоскость в пространстве.
- •3.1. Область определения функции.
- •3.2. Непрерывность функции, точки разрыва.
- •3.3. Производные высших порядков.
- •3.4. Дифференциальное исчисление фнп.
- •3.5. Основные методы интегрирования.
- •3.6. Свойства определенного интеграла.
- •4.1. Числовые последовательности.
- •4.2. Сходимость числовых рядов.
- •4.3. Область сходимости степенного ряда.
- •4.4. Ряд Тейлора (Маклорена).
- •5.1. Типы дифференциальных уравнений.
- •5.2. Однородные дифференциальные уравнения.
- •5.3. Задача Коши для дифференциального уравнения первого порядка.
- •5.4. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •6.1. Определение вероятности.
- •6.2. Теоремы сложения и умножения вероятностей.
- •6.3. Законы распределения вероятностей дискретных случайных величин
- •6.4. Числовые характеристики случайных величин
- •7.1. Характеристики вариационного ряда.
- •7.2. Интервальные оценки параметров распределения.
- •7.3. Элементы корреляционного анализа.
- •7.4. Проверка статистических гипотез.
- •8.1. Линейное программирование: аналитическое задание области допустимых решений.
- •8.2. Транспортная задача.
- •8.3. Теория игр: матричные игры.
- •8.4. Сетевое планирование и управление.
- •9.1. Функция полезности.
- •9.2. Производственные функции.
- •9.3. Коэффициенты эластичности.
- •9.4. Статическая модель межотраслевого баланса.
Дидактические единицы |
стр. |
ДЕ 1. Линейная алгебра |
2 |
1.1. Вычисление определителей |
2 |
1.2. Умножение матриц |
6 |
1.3. Определение линейного пространства |
11 |
1.4. Квадратичные формы |
13 |
ДЕ 2. Аналитическая геометрия |
19 |
2.1. Полярные координаты на плоскости |
19 |
2.2. Прямая на плоскости |
23 |
2.3. Кривые второго порядка |
27 |
2.4. Плоскость в пространстве |
30 |
ДЕ 3. Дифференциальное и интегральное исчисление |
36 |
3.1. Область определения функции |
36 |
3.2. Непрерывность функции, точки разрыва |
41 |
3.3. Производные высших порядков |
44 |
3.4. Дифференциальное исчисление ФНП |
49 |
3.5. Основные методы интегрирования |
52 |
3.6. Свойства определенного интеграла |
57 |
ДЕ 4. Ряды |
63 |
4.1. Числовые последовательности |
63 |
4.2. Сходимость числовых рядов |
67 |
4.3. Область сходимости степенного ряда |
72 |
4.4. Ряд Тейлора (Маклорена) |
76 |
ДЕ 5. Дифференциальные уравнения |
82 |
5.1. Типы дифференциальных уравнений |
82 |
5.2. Однородные дифференциальные уравнения |
86 |
5.3. Задача Коши для дифференциального уравнения первого порядка |
90 |
5.4. Дифференциальные уравнения высших порядков, допускающие понижение порядка |
95 |
ДЕ 6. Теория вероятностей |
101 |
6.1. Определение вероятности |
101 |
6.2. Теоремы сложения и умножения вероятностей |
105 |
6.3. Законы распределения вероятностей дискретных случайных величин |
109 |
6.4. Числовые характеристики случайных величин |
113 |
ДЕ 7. Математическая статистика |
119 |
7.1. Характеристики вариационного ряда |
119 |
7.2. Интервальные оценки параметров распределения |
121 |
7.3. Элементы корреляционного анализа |
124 |
7.4. Проверка статистических гипотез |
127 |
ДЕ 8. Экономико-математические методы |
130 |
8.1. Линейное программирование: аналитическое задание области допустимых решений |
130 |
8.2. Транспортная задача |
137 |
8.3. Теория игр: матричные игры |
145 |
8.4. Сетевое планирование и управление |
149 |
ДЕ 9. Экономико-математические модели |
154 |
9.1. Функции полезности |
154 |
9.2. Производственные функции |
158 |
9.3. Коэффициенты эластичности |
162 |
9.4. Статическая модель межотраслевого баланса |
166 |
Структура теста
ДЕ 1. Линейная алгебра |
1.1. Вычисление определителей |
1.2. Умножение матриц |
1.3. Определение линейного пространства |
1.4. Квадратичные формы |
1.1. Вычисление определителей.
![]() ЗАДАНИЕ
N 20 сообщить
об ошибке
Тема:
Вычисление определителей
Определитель
ЗАДАНИЕ
N 20 сообщить
об ошибке
Тема:
Вычисление определителей
Определитель 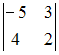 равен
…
равен
…
|
|
|
– 22 |
|
|
|
2 |
|
|
|
|
|
|
|
22 |
Решение:
Определитель
второго порядка вычисляется по формуле:
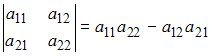 .
Тогда
.
Тогда 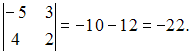
ЗАДАНИЕ
N 25 сообщить
об ошибке
Тема:
Вычисление определителей
Корень
уравнения 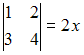 равен
…
равен
…
|
|
|
– 1 |
|
|
|
5 |
|
|
|
1 |
|
|
|
– 5 |
Решение:
Определитель
второго порядка вычисляется по формуле:
.
Тогда 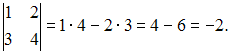 По
условию задачи определитель должен
равняться
По
условию задачи определитель должен
равняться ![]() то
есть
то
есть ![]() Следовательно,
Следовательно, ![]()
ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Вычисление определителей
Корень
уравнения 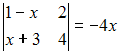 равен
…
равен
…
|
|
|
– 1 |
|
|
|
– 5 |
|
|
|
1 |
|
|
|
5 |
Решение:
Определитель
второго порядка вычисляется по формуле:
.
Тогда 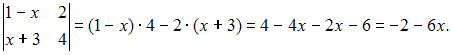 По
условию задачи определитель должен
равняться
По
условию задачи определитель должен
равняться ![]() то
есть
то
есть ![]() Следовательно,
Следовательно,
ЗАДАНИЕ
N 23 сообщить
об ошибке
Тема:
Вычисление определителей
Определитель 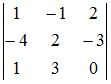 равен
…
равен
…
|
|
|
– 16 |
|
|
|
– 22 |
|
|
|
– 26 |
|
|
|
– 8 |
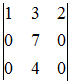
Решение:
Вычислим
определитель, например, разложением по
первой строке:
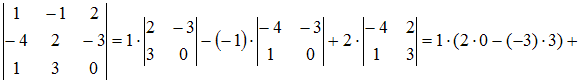
![]()
ЗАДАНИЕ
N 37 сообщить
об ошибке
Тема:
Вычисление определителей
Корень
уравнения 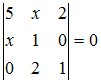 равен
…
равен
…
|
|
|
– 1 |
|
|
|
1 |
|
|
|
– 5 |
|
|
|
3 |
Решение:
Определитель
третьего порядка можно вычислить,
например, разложением по элементам
первой строки:
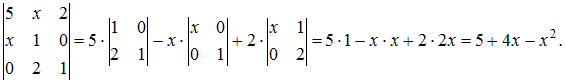 По
условию задачи определитель должен
равняться 0, то есть
По
условию задачи определитель должен
равняться 0, то есть ![]() Следовательно,
Следовательно, ![]()
ЗАДАНИЕ
N 33 сообщить
об ошибке
Тема:
Вычисление определителей
Определитель 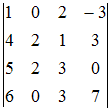 равен
…
равен
…
|
|
|
0 |
|
|
|
– 144 |
|
|
|
144 |
|
|
|
1 |
Решение:
Воспользуемся
свойствами определителей, например, к
элементам третьей строки прибавим
элементы первой строки, умноженные на
(–1):
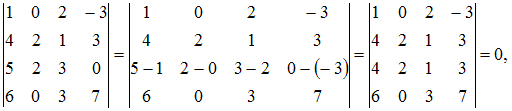 так
как определители с одинаковыми строками
равны нулю.
так
как определители с одинаковыми строками
равны нулю.
ЗАДАНИЕ
N 35 сообщить
об ошибке
Тема:
Вычисление определителей
Разложение
определителя 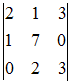 по
строке может иметь вид …
по
строке может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Определитель
третьего порядка можно вычислить,
например, разложением по элементам
первой строки:
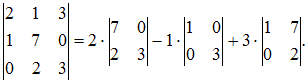
ЗАДАНИЕ N 11 сообщить об ошибке Тема: Вычисление определителей Определитель не равный нулю может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
каждый из определителей, например,
разложением по первой строке:
1) 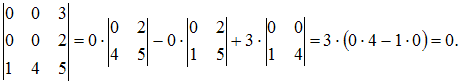 2)
2) 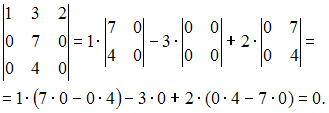 3)
3) 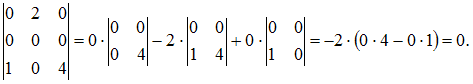 4)
4)