belyuchenko_i_s_smagin_a_v_i_dr_analiz_dannykh_i_matematiche

вестный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство питания растет со временем линейно (в арифметической прогрессии). Из этого он сделал справедливый вывод, что рано или поздно экспонента обязательно «обгонит» линейную функцию, и наступит голод.

Модель Мальтуса описывает ситуацию, когда среда не оказывает ограничивающего влияния на плотность, и специфическая скорость роста популяции (r) для данных микроклиматических условий постоянна и максимальна. Хотя в общем случае биотический потенциал зависит от времени t, численности или плотности популяции N.

Это одна из первых моделей, в которой динамика численности или плотности популяции N(t) описывается дифференциальным уравнением:

где r – биотический (репродуктивный) потенциал или так называемый мальтузианский параметр роста.

Решим дифференциальное уравнение (12.7), разделяя переменные:

где N0 – численность в нулевое время;

Nt – численность в момент времени t;

e – основание натуральных логарифмов;

r – репродуктивный потенциал популяции.

171

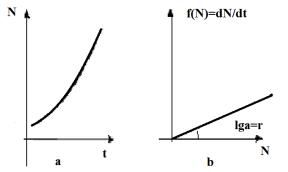
Графически модель представляет собой неограниченную кривую (Рисунок 12.2, а). Зависимость скорости роста популяции от ее численности представляет собой линейную функцию (Рисунок 12.2, b). Между величинами r (скорость роста популяции) и N очень часто наблюдается статистически достоверная обратная зависимость (интересно, что единственная популяция, у которой отмечена статистически достоверная положительная зависимость этих параметров – это популяция человека!).

Рисунок 12.2 – Экспоненциальный рост. Зависимость численности от времени (а) и скорости роста от численности (б)

Модель Мальтуса послужила одним из отправных пунктов для Ч. Дарвина при создании теории эволюции видов. В фитоценологии эта модель используется, например, при описании скорости кругооборота числа видов в сообществе в ходе сукцессии, процесса накопления фитомассы древостоев (правда, в этом случае введена эмпирическая отрицательная зависимость r от t; Лиепа, 1970). Большое практическое применение эта модель имеет в биотехнологии (например, для установления оптимальных режимов выращивания различных микроорганизмов).

172

Примером экспоненциального роста может служить размножение видов, завезенных в места, где имеется много пищи и отсутствуют конкурирующие виды и хищники (кролики в Австралии).

12.7Пример расчета мальтузианского параметра по экспериментальным данным

С целью изучения динамики эвтрификации водоемов, загрязненных минеральными удобрениями, в пяти прудах моделировали размножение сине-зеленых водорослей в нелимитированных условиях. Полученные данные об изменении численности популяции водорослей в каждом пруду представлены в таблице 12.2.

Таблица 12.2 – Изменение численности популяции водорослей в 5-ти прудах

На основе этих данных необходимо определить для популяции водорослей в каждом пруду значение мальтузианского параметра r (удельной скорости размножения) и период удвоения T. Найти также соответствующие медианы по полученным выборкам r и T.

173

Решение. Для обработки экспериментальных данных используем логарифмическую форму этого уравнения:

ln xt rt . x0

Для этого каждый элемент столбцов с данными по численности сине-зеленых водорослей необходимо разделить на соответствующий начальный элемент и взять натуральный логарифм этого отношения (таблица 12.3).

Таблица 12.3 – Промежуточные расчеты для мальтузианского параметра

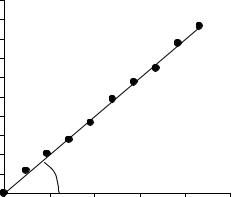
Затем для каждого пруда на основе таблицы 12.3 следует построить график, где по оси х откладывается время, а по оси у – соответствующее значение ln(xt/x0), как это показано на рисунке 12.3. Экспериментальные данные должны сгруппироваться около прямой линии, тангенс угла которой и есть искомое значение мальтузианского параметра r .

Значение периода удвоения T находим по формуле:

T ln 2 . r

174

Результаты обработки данных в этой задаче представлены в таблице 12.4.

Рисунок 12.3 – Линеаризация экспоненциальной зависимости.

Таблица 12.4 – Результаты расчета мальтузианского параметра сине-зеленых водорослей

Медиану определяем обычным способом как срединное значение в выборке: Ме(r) = 0,0198 час-1, Ме(T) = 35 час.

Более простой способ непосредственной оценки r – аппроксимация экспериментальных данных экспоненциальной функцией из стандартного пакета MS EXCEL (см. главу 7)

12.8 Модель логистического роста

Модель логистического роста (Ферхюльста – Пирла) лежит в основе формализации закона ограниченного роста

175

Дарвина: окружающая среда действует как лимитирующий фактор на биоценотический потенциал популяции.

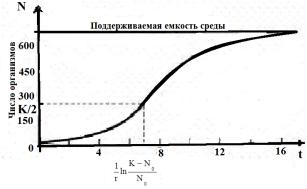
Воздействие экологических факторов на скорость роста популяции может довести численность популяции до стабильной (r = 0) либо ее уменьшить. Экспоненциальный рост замедляется или останавливается полностью, и J-образная кривая как бы превращается в S – образную (логистическую) кривую (Рисунок 12.4).

Рисунок 12.4 – Ограниченный рост популяции

При начальной численности N0, близкой к нулю, скорость роста имеет максимальное значение rmax, а при предельной численности r = 0 (Рисунок 12.4). Внутривидовая конкуренция, влияя на рождаемость и плотность, регулирует популяцию, поддерживая ее плотность на стабильном уровне, при котором рождаемость уравновешена смертностью. Такую плотность называют «предельной нагрузкой на среду», или «емкостью среды» и обозначают К.

Емкость среды – это та плотность популяции, которая в данных условиях среды может поддерживаться на постоянном уровне. К факторам, ограничивающим рост популяции можно отнести внутривидовую конкуренцию за ре-

176

сурс (пищу, свет) или же накопление отбросов жизнедеятельности.

.

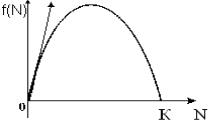
Рисунок 12.5 – Логистический рост. Зависимость скорости роста от численности

Кривая N(t) имеет точку перегиба с координатами

Ордината точки перегиба представляет собой половину максимальной численности, а абсцисса зависит как от емкости популяции K, так и от константы собственной скорости роста r: чем выше генетические возможности популяции, тем скорее наступает перегиб на кривой численности. Точка перегиба представляет собой координату, где наблюдается наибольшая скорость популяции (см. рисунок 12.5).

Логистическое уравнения можно записать несколькими способами. В классической форме оно выглядит следующим образом:

где ε – биотический потенциал популяции; γ – коэффициент внутривидовой конкуренции;

x – численность или плотность популяции.

177

Удобно еще пользоваться такой формой записи:

Модель (12.9) имеет простое аналитическое решение, и плотность популяции в зависимости от времени можно вычислять непосредственно по следующей формуле:

График функции Nt представляет собой S-образную кривую (Рисунок 12.4). Для практических целей полезно помнить формулы, связывающие коэффициенты модели:

где К – емкость среды;

r (ε)– биотический потенциал;

γ – коэффициент внутривидовой конкуренции.

Несмотря на схематичность положенных в ее основу представлений, логистическая кривая оказалась очень хорошим приближением для описания кривых роста многих популяций. Например, в демографии для прогноза численности населения предпринимались попытки подобрать логистические кривые для данных о численности населения различных стран. Благодаря применению математики обсуждение этих проблем становится более конкретным, но к оценке результатов, получаемых с их помощью, необходимо подходить с большой осторожностью. Модель может быть приближенно справедливой для периода, по которому имеются данные, но это не гарантирует ее справедливости в бу-

178

дущем. Окружающая среда и социальные условия могут измениться, и, следовательно, изменятся скорости размножения и гибели и коэффициент замедления роста.

Оценка мальтузианского параметра роста в моделях 12.7 и 12.9 приводит к различным результатам, что надо помнить при количественном анализе закономерностей численности популяций. Так в главе 7 приводятся результаты оценки r для роста водорослей в водной среде (Рисунок 7.8) по логистической модели в помощью программы нелинейной регрессии в компьютерной среде S-Plot. Он, как помним, получился равным 0,03 час-1. Тогда как для той же последовательности экспериментальных данных для начальной (экспоненциальной) фазы роста оценка по модели Мальтуса дала величину 0,02 час-1, то есть в 1,5 раза меньшую (таблица 12.4). Поэтому при моделировании роста лучше непосредственно определять этот важный параметр с помощью аналитического решения уравнения ФерхюльстаПирла (12.11), как это было показано в главе 7.

12.9Дискретный аналог дифференциальных уравнений роста популяции

Один из вариантов моделирования динамики популяций основан на применении разностных уравнений, которые соответствуют способу получения исходных данных в дискретные интервалы времени. Разностные уравнения очень удобны для реализации моделей на компьютере. Выбор дифференциальных уравнений или разностных для моделирования динамики популяций зависит от того, что интересует в данной задаче: характер изменения некоторой величины, или скорость ее изменения. В последнем случае используют дифференциальные уравнения.

Рассмотрим простейшую из моделей для вида с дискретными периодами размножения, в которой численность

179

популяции в момент времени t равна Nt и изменяется во времени пропорционально величине основной чистой скорости воспроизводства R. Данная модель может быть выражена уравнением:

решение которого имеет вид:

Коэффициент воспроизводства связан с биотическим

потенциалом следующей формулой R er . Поэтому можно формулу (12.12) записать так:

При росте численности популяции R должна быть больше 1, а r – больше 0.

Для уравнения логистического роста разностное уравнение имеет вид:

где r – константа собственной скорости роста, К – емкость экологической ниши популяции.

Поведение во времени переменной Nt+1 в зависимости от величины параметра r может носить характер не только монотонного роста, как было для непрерывной модели, но также быть колебательным или квазистохастическим, как это изображено на рисунке 12.6.

Для небольших r численность популяции стремится к устойчивому равновесию. При величине параметра r > 2,6 начинается хаотизация решений через двухточечный предельный цикл. При достаточно больших r динамика численности демонстрирует хаотические всплески. Уравнения та-

180