
belyuchenko_i_s_smagin_a_v_i_dr_analiz_dannykh_i_matematiche
.pdf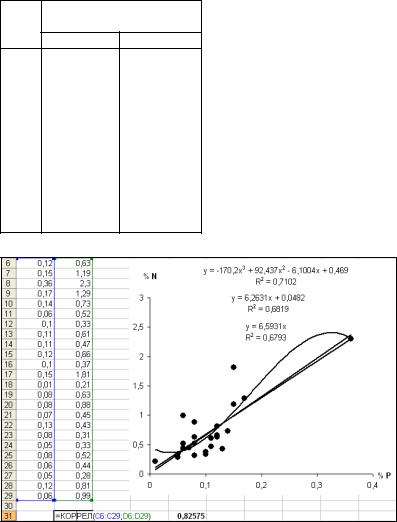
Таблица 6.2 – Взаимосвязь между общим количеством фосфора и азота в почве
№Общее количество,
%сухого вещества
п/п фосфора азота
1 |
0,12 |
0,63 |
2 |
0,15 |
1,19 |
3 |
0,36 |
2,3 |
4 |
0,17 |
1,29 |
5 |
0,14 |
0,73 |
6 |
0,06 |
0,52 |
7 |
0,1 |
0,33 |
8 |
0,11 |
0,61 |
9 |
0,11 |
0,47 |
10 |
0,12 |
0,66 |
11 |
0,10 |
0,37 |
12 |
0,15 |
1,81 |
№ |
Общее количество, |
|
п/п |
% сухого вещества |
|
|
фосфора |
азота |
13 |
0,01 |
0,21 |
14 |
0,08 |
0,63 |
15 |
0,08 |
0,88 |
16 |
0,07 |
0,45 |
17 |
0,13 |
0,43 |
18 |
0,08 |
0,31 |
19 |
0,05 |
0,33 |
20 |
0,08 |
0,52 |
21 |
0,06 |
0,44 |
22 |
0,05 |
0,28 |
23 |
0,12 |
0,81 |
24 |
0,06 |
0,99 |
Рисунок 6.1 – Связь между общим количеством фосфора и азота в почве (фрагмент листа MS EXCEL).
61

6.4Интерпретация коэффициента корреляции
Следует знать, что выводы о пределах изменения для rxy справедливы только в определенной статистической модели. Для исключения возможных ошибок содержательной интерпретации коэффициента корреляции должен сопутствовать визуальный анализ диаграммы рассеяния (графиков). Ранее уже подчеркивалось, что rxy измеряет тесноту только линейной связи между переменными х и у. Поэтому для диаграммы рассеяния на рисунке 6.2 rxy ≈ 0. Однако rxy ≈ 0 и для диаграммы рассеяния, приведенной на рисунке 6.3, несмотря на то, что в этом случае имеет место функциональная связь.
Рисунок 6.2 – Отсутствие линейной связи
Рисунок 6.3 – Нелинейная функциональная зависимость
62

Происходит это из-за нелинейной связи между х и у. Этот пример должен служить предостережением против опрометчивого вывода о том, что равенство нулю коэффициента корреляции между переменными х и у всегда свидетельствуют об отсутствии статистической связи между ними.
С другой стороны возможен вариант возникновения ложной корреляции в связи с появлением в совокупности исходных данных аномальных значений. Это бывает по следующим причинам:
–неоднородность анализируемого материала;
–ошибки при регистрации данных;
–когда исследователь случайно выбирает из всего множества экспериментальных данных некоторый набор, в котором пары величин изменяются однонаправленно.
Значение коэффициента корреляции может быть высоким, но не достоверным, случайным. Чтобы проверить
статистическую значимость коэффициента корреляции,
необходимо рассчитать эмпирическое (наблюдаемое) значение t-критерия. Для малых выборок n < 100 оно рассчитывается по формуле:
|
|
|
|
|
|
|
|
tнабл |
|
r |
n 2 |
(6.2) |
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
1 r 2 |
||||||
|
|
|
|
||||
При n > 100 формула для расчета t-наблюдаемого следующая:
tнабл |
|
r |
|
n |
|
(6.3) |
|
|
|
|
|||
1 r 2 |
|
|||||
|
|
|
||||
Критическое значение t-критерия Стьюдента рассчитывается по специальной таблице или в EXCEL с помощью встроенной функции СТЬЮДРАСПОБР в соответствии с
63
принятым уровнем значимости и числом степеней свобо-
ды f = n – 2: tкрит( , f n 2) .
При tнабл tкрит нулевая гипотеза о равенстве нулю коэффициента корреляции между изучаемыми признаками в генеральной совокупности отвергается, и r считается статистически значимым на принятом уровне значимости.
При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэффициенты сводят в таблицы (корреляционные матрицы), в которых на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.
6.5 Ранговый коэффициент корреляции Спирмена
Если какое-либо из условий по ограничению использования коэффициента корреляции Пирсона не выполняется (все переменные должны быть непрерывными, данные должны являться случайной выборкой из генеральной совокупности с нормальным распределением, зависимость близка к линейной), применяются так называемые непараметрические критерии и, в частности, коэффициент ранговой корреляции Спирмена. Его значение также заключено между –1 и +1. Кроме того, этот коэффициент используется при оценки взаимосвязи между признаками, хотя бы один из которых оценивается качественно. Формула для его вычисления выглядит так:
|
n |
di2 |
(6.4) |
r |
i 1 |
, |
|
n3 n |
|
||
где di – разность рангов по обоим признакам i-го объекта; n – число объектов.
64

Пример. Рассмотрим пример вычисления рангового коэффициента корреляции. Изучается взаимосвязь между уровнем урбанизации и степенью загрязнения окружающей среды. Для этого эксперт или группа экспертов оценивают совокупность городов с разной степенью урбанизации по уровню загрязненности окружающей среды и упорядочивают все города по обоим показателям. Процесс упорядочивания носит название ранжирования, т. е. приписывания каждому городу ранга – порядкового номера, который соответствует месту, занимаемому им во всей совокупности. Такое ранжирование проводится по обоим интересующим нас признакам.
Обозначим города буквами от А до К и выпишем для них следующие две последовательности рангов (таблица
6.3).
Таблица 6.3 – Ранжирование городов по степени урбанизации и степени загрязненности
Города |
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Степень |
3 |
7 |
5 |
9 |
1 |
8 |
6 |
10 |
4 |
2 |
урбанизации |
|
|
|
|
|
|
|
|
|
|
Уровень |
2 |
4 |
3 |
5 |
1 |
9 |
8 |
10 |
7 |
6 |
загрязненно- |
|
|
|
|
|
|
|
|
|
|
сти |
|
|
|
|
|
|
|
|
|
|
Разности di |
1 |
3 |
2 |
4 |
0 |
-1 |
-2 |
0 |
-3 |
-4 |
Разности di2 |
1 |
9 |
4 |
10 |
0 |
1 |
4 |
0 |
9 |
1 |
|
|
|
|
|
|
|
|
|
|
6 |
Тогда
rsp 1 9 4 16 03 1 4 0 9 16 0,6 . 10 10
Значение полученного коэффициента указывает на довольно высокую степень согласованности между степенью урбанизации и уровнем загрязненности среды в городах.
65

6.6 Коэффициент взаимной сопряженности
Кроме признаков, выраженных количественно или допускающих ранжирование, встречаются и такие, относительно которых можно утверждать только то, имеются ли они у данного объекта или отсутствуют. При этом наличие или отсутствие определенного признака обозначается нулем или единицей (битовые данные). Для данных, представленных в таком виде, также существует коэффициент, который позволяет оценивать корреляцию между ними:
рху рх ру ,
рх qх ру qу
(6.5)
где рх и ру – доля объектов, имеющих единицу по признакам х и у соответственно;
qx и qy – доля объектов, имеющих нуль по признакам х и у соответственно;
рху – доля объектов имеющих одновременно единицу и по х и по у.
Очевидно, что рх + ру = qx + qy = 1
Формула 6.5 вытекает их формулы для обычного коэффициента корреляции (6.1), если в последнюю вместо х и у подставить соответствующие значения, выраженные в долях.
Пример. Пусть имеются данные об условиях гнездования двух видов чаек: серебристых и сизых. Совершенно произвольно серебристых будем обозначать как 1, а сизых – как 0. Каждый из этих видов может гнездоваться в камнях
(1) и в других местах (0). Обследование дало следующие данные (таблица 6.3):
Таблица 6.3 – Условия гнездования двух видов чаек
Вид чайки |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Место гнездо- |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
вания |
|
|
|
|
|
|
|
|
|
|
|
|
66
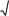
Имеем рх = |
7/12; |
|
|
|
|
||||
py |
= |
4/12; |
|
|
|
|
|
|
|
qx |
= |
5/12; |
|
|
|
|
|
|
|
qy |
= |
8/12; |
|
|
|
|
|
|
|
pxy |
= |
3/12. |
|
|
|
|
|
|
|
По формуле (6.5) имеем: |
|
|
|
|
|||||
|
|
|
|
|
0,25 0,583 0,33 |
|
|
0,056 |
0,24 . |
|
|
|
|
|
|
|
|||
|
|
0,583 0,417 0,333 0,667 |
0,232 |
||||||
|
|
|
|
|
|
|
|||
6.7 Определение значимости показателей
Статистическая значимость результата анализа представляет собой оцененную меру уверенности в его «истинности» (в смысле «репрезентативности выборки»). Выражаясь технически, -уровень (этот термин был впервые использован в работе Brownlee, 1960) – это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий -уровень соответствует более низкому уровню доверия к результатам анализа. Именно, -уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого признака на всю популяцию.
Например, -уровень, равный 0,05 (т. е. 1/20) показывает, что имеется 5 %-я вероятность, что найденная в выборке связь между переменными (если изучается взаимосвязь между переменными) является лишь случайной особенностью данной выборки.
Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать «значимым». Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, является произвольным.
На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т. е. до прове-
67
дения опыта) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований.
Обычно во многих областях результат = 0,05 является приемлемой границей статистической значимости, однако следует помнить, что этот уровень все еще включает довольно большую вероятность ошибки (5 %). Результаты, значимые на уровне = 0,01 обычно рассматриваются как статистически значимые, а результаты с уровнем = 0,005 или = 0,001 как высоко значимые.
68
Глава 7. РЕГРЕССИОННЫЙ АНАЛИЗ И АППРОКСИМАЦИЯ ДАННЫХ
7.1 Задачи регрессионного анализа
Довольно часто в практике исследовательской работы имеет место ситуация, когда важнейшие переменные, описывающие некоторый процесс, известны заранее, но модель процесса еще не известна. В этом случае возможны разные подходы. Одним из них является построение эмпирических моделей, которое осуществляется с помощью регрессионного анализа. Регрессионная модель в зависимости от входящих в нее факторов (хj) может быть использована:
–для управления объектом;
–для прогнозирования его состояния;
–для объяснения физики явлений. Регрессионный анализ позволяет:
–производить расчет регрессионных моделей путем определения значений параметров – постоянных коэффициентов при независимых переменных – регрессорах, которые часто называют факторами;
–проверять гипотезу об адекватности модели имеющимся наблюдениям;
–использовать модель для прогнозирования значений зависимой переменной при новых или ненаблюдаемых значениях независимых переменных.
Среди регрессионных моделей обычно выделяют однопараметрические модели и многопараметрические модели, а также модели, линейные относительно независимых переменных, нелинейные по переменным и нелинейные по параметрам.
7.2Примеры регрессионных моделей в экологии
1. Скорость поглощения кислорода опадом листьев [Джефферс Дж.,1981]:
69

lg(Y+1) = 0,561– 8,701D 10-4 + 3,935D2 10-7 + 7187B 10-4 + 0,0398T,
где: Y – поглощение кислорода, измеренное в мкл (0,25 г)-1ч-1; D – число дней, в течение которых выдерживались образцы;
B – процентное содержание влаги в образцах; Т – температура, Со.
Эта формула дает оценки для скорости поглощения кислорода во всем диапазоне дней, температур и влажностей, которые наблюдались в эксперименте, со средним квадратичным отклонением в поглощении кислорода, равном S =
0,319 ± 0,321.
2. Зависимость средней концентрации SO2 (мг∙м-3) от освещенности на высоте 1,5 м (Q), средней высоты мха на стволе (h, мм), степени покрытия древесной растительности лишайником (р, %) [Андерсен Дж. М., 1985]:
SO2 = 18,72 – 3,94Q – 0,15h – 2,38р.
Это уравнение регрессии описывает 72 % дисперсии ряда и таким образом, применяется для прогноза изменения концентрации SO2. (Коэффициенты рассчитаны для Великобритании. Для других районов константы следует рассчитывать эмпирическим путем).
7.3 Линейные регрессионные модели
Наиболее простые для построения и анализа линейные модели как однопараметрические, так и многопараметрические. Они содержат независимые переменные только в первой степени. Большая их часть основана на предположении о нормальном распределении данных или ошибок наблюдений, поэтому в каждом случае анализа необходима предварительная проверка соответствия данных нормальному распределению.
Модель простой линейной регрессии имеет вид:
70
