belyuchenko_i_s_smagin_a_v_i_dr_analiz_dannykh_i_matematiche

Отсюда оценка плотности популяции может быть рассчитана, как:

если подсчитывалось число пробных площадок, на которых не встречено ни одного объекта, или:

если подсчитывалось число пробных площадок, на которых был встречен хотя бы один объект.

Точность данного метода, естественно, повышается с увеличением количества пробных площадок.

Поскольку для распределения Пуассона среднее ариф-

метическое равно его дисперсии (то есть, X S 2 ), то ошибку оценки средней плотности можно найти по формуле:

Если вместо большого числа небольших пробных площадок площадью R использовать одну ленточную трансекту площадью R1 = n·R , то количество объектов, зарегистрированных в пределах трансекты (N), отнесенное к ее площади (R1), даст оценку абсолютной плотности (X):

На основании особенностей распределения Пуассона оценку ошибки показателя плотности популяции в данном случае можно получить следующим образом:

141

При большой численности объектов, зарегистрированных на территории одной трансекты (или на нескольких десятках пробных площадок), доверительные интервалы оценки плотности рассчитываются по формуле: X 1,96 mx

Но при небольших значениях плотности, когда распределение Пуассона становится резко асимметричным, доверительный интервал для общего числа объектов (особей, нор, гнезд и т.п.), зарегистрированных на исследуемой территории, рассчитывается по следующим формулам:

где N – количество объектов, зарегистрированных в пределах трансекты; Nн и Nв – нижняя и верхняя границы показателя;

χ2 – табличное значение критерия Хи-квадрат Пирсона с заданным числом степеней свободы (df), и уровнем значимости α.

11.3Оценка адекватности модели распределения организмов в пространстве

Согласованность эмпирического распределения с Пуассоновским проверяется с помощью критерия 2 .

χ2 расчетное определяется как сумма частных от деления квадратов отклонений фактически полученных частот от ожидаемых на число ожидаемых.

Если наблюдаемые и ожидаемые значения совпадают довольно хорошо ( p2 st2 ), то можно сделать вывод, что

142

распределение организмов по участку близко к случайному. В противном случае ( p2 st2 ), будет неслучайное или аг-

регированное распределение. В первом случае если, например, среднее число особей на квадрат равно трем, то квадратов с тремя особями будет слишком много по сравнению с ожидаемым числом. Квадратов же, в которых нет ни одной особи или, наоборот, много особей, будет слишком мало, так как они вынуждены разместиться более равномерно по участку.

Во втором случае будет слишком много как пустых квадратов, так и квадратов с большим количеством особей.

Чтобы пользоваться критерием 2 , необходимо соблюдать следующие условия:

–объем выборочной совокупности должен быть достаточно большой (например, общее число пересчитанных животных или растений n > 50);

–в каждой рассчитанной группе должно быть не менее пяти наблюдений (например, число квадратов с n животными должно быть не менее пяти);

–для вычисления 2 используют только численности, а

не проценты или величины, полученные при взвешиваниях. Пример. На исследуемом участке было расставлено 543

совершенно одинаковых ловушки для мелких млекопитающих. По прошествии некоторого времени в ловушках было обнаружено:

Спрашивается – согласуется ли распределение животным по исследуемой площади со случайным?

Схема решения.

Общее число животных:

143

n = 0∙468 + 1∙41 + 2∙16 + 3∙11 + 4∙2 + 5∙4 + 6∙0 + 7∙1 =141; n·p = 141∙1/543 = 0,26.

Теперь, используя ряд Пуассона, можно определить ожидаемые доли ловушек с одним, двумя, тремя, и т. д. животными, в предположении, что все ловушки равно эффективны. После чего находим ожидаемое число ловушек с определенным количеством животных.

Поскольку число ловушек с четырьмя, пятью, шестью, семью и восмью животными меньше пяти, то их можно объединить в один класс.

Ожидаемая доля ловушек, в которых нет ни одного животного, равна e–m = e–0,26 = 0,77. Ожидаемое число ловушек, в которых нет ни одного животного 0,77·543 ≈ 418,1.

Аналогично определяют ожидаемые доли и число ловушек с одним, двумя, тремя животными. Ожидаемую долю ловушек с числом животных от 4 до 8 можно определить по формуле: 1 – Р(0) – Р(1) – Р(2) – Р(3) = 1–0,77– 0,20 – 0,026 – 0,002 = 0,002.

Тогда критерий χ2р будет следующей суммой:

Число степеней свободы df = 5 – 2 = 3.

Для = 0,05 χ2т = 7,81. 169,05 > 7,81.

Следовательно, χ2р > χ2т. Отсюда будет неслучайное или агрегированное распределение животных по территории исследуемого участка.

144

11.4 Индекс Одума

Наиболее простым методом определения характера пространственного распределения объектов является использо-

вание индекса Одума ( I O ) (Одум, 1986):

O X

Напомним, что S2 – дисперсия для переменной величины (численности) х рассчитывается при известном значении средней численности (Х) и общем количество исследованных пробных площадок n как:

группами и, наконец, если IO 1 , то особи распределенные

случайным образом.

Уровень значимости индекса Одума можно оценить, сравнивая рассчитанное значение I O с табличным значением F-критерия Фишера – Снедекора с числом степеней сво-

боды df1 df2 n 1.

В тех случаях, если X S 2 , рассчитывается обратная

величина — X / S 2 , которая затем сравнивается с табличным значением F-критерия Фишера – Снедекора с числом степеней свободы df1 df2 n 1. Если рассчитанное зна-

чение Io или его обратная величина превышает табличное значение F-критерия, то распределение статистически значимо отличается от случайного (когда отношение дисперсии

145

к средней величине равно 1). Тогда его считают равномерным, если IO 1 и групповым, если IO 1.

Анализ индекса Одума S2/Х показывает, что он, вопервых, имеет размерность (равную численности на единичный элемент пространства), а во-вторых – будет зависеть от численности, особенно при высоких величинах дисперсии, так как числитель (дисперсия) – квадратичная функция, а знаменатель – линейная. В теории пространственного распределения вводятся ограничения на минимальное число площадок учета, что наряду с естественным ограничением числа видов на единице площади в экосистемах планеты позволяет использовать индекс Одума, несмотря на проблемы, связанные с численностью. По-видимому, корректнее использовать безразмерный индекс S/Х, то-есть отношение не дисперсии, а стандартного отклонения к среднему. Тогда будут соблюдаться и критерии Одума (S/Х →0 – равномерное, S/Х 1 – случайное, S/Х >1 – контагиозное распределения) и не будет обозначенных выше проблем с численностью видов.

11.5 Модели распределения значимости видов

Значимость представляет собой группу оценок, с помощью которых виды в сообществе могут сравниваться друг с другом.

Значение отдельных видов должно определяться тем, какую роль играют они в функционировании экосистемы или в продукционном процессе.

Но при исследованиях сообществ установить истинную функциональную роль видов нелегко, если об их значении судить только по обилию, т. е. численности и биомассе. Наиболее пригодной оценкой является продукция. Она отражает меру использования ресурсов видов для роста попу-

146

ляции и позволяет сравнивать в одной шкале виды, значительно различающиеся по размерам и типам.

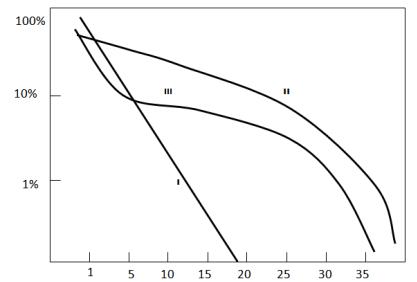
Чтобы узнать, как разграничивается пространство ресурсов сообщества и каким образом формируется количественные соотношения между продукцией видов (или другими оценками значимости), можно построить следующий график: по оси ординат откладывается относительная значимость в процентах, а по оси х – ранжированная последовательность видов от наиболее до наименее обильного.

Полученная в 1965 г. кривая названа Р. Уиттекером

[1980] «кривой доминирования – разнообразия», а Э. Пианкой [1978] – «кривой значимости видов». Предложен ряд гипотез для толкования этих кривых, которые нашли выражение в моделях рангового распределения. Следует заметить, что эмпирические результаты не совпадают полностью ни с одной из трех выдвинутых гипотез.

Геометрический ряд. Графически модель имеет вид прямой линии (на рисунке 11.1, кривая I). Описывается ситуация, когда каждый последующий вид занимает ровно половину доступного пространства ниши, что соответствует

гипотезе «перехвата» экологических ниш или геометриче-

скому ряду И. Мотомуры. Пример такого ряда: наиболее обильный вид в два раза многочисленнее следующего за ним по обилию, а этот последний в свою очередь вдвое многочисленнее третьего и т. д. Можно предположить, что в этом случае доминирующий вид занимает половину доступного пространства ниш, второй – половину оставшегося пространства (1/4 исходного) и т. д. Таким образом, каждый вид занимает прежде всего свободную нишу, не перекрывающуюся с другими. Формализуется этот закон следующим уравнением:

где n(k) – значимость вида k в ряду от k = 1 (наиболее значимый вид) до k = M (наименее значимый вид);

147

Сk(k 1) n(k) / n(k 1) – отношение значимости каждого вида к

каждому предшествующему ему виду;

n1 – значимость первого и наиболее значимого вида.

Рисунок 11.1 – Кривые значимости видов:

I – геометрический ряд; II – модель «разломанного стержня» МакАртура; III – логнормальное распределение (модель Престона)

Модель содержит два параметра: n1 – обилие 1-го, наиболее обильного вида; и Ck(k-1) – доля обилия i-го вида от обилия предыдущего. Параметр Ck(k-1) модели отражает степень выравненности видовой структуры и может служить индексом видового разнообразия.

При геометрическом распределении доминируют немногие виды при очень низкой численности большинства. Распределение обилий видов по типу геометрической модели обнаруживается преимущественно в бедных видами местообитаниях или в сообществах на очень ранних стадиях сукцессии. Такое распределение характерно для некоторых

148

растительных сообществ в суровых условиях окружающей среды (например, сообщество растений субальпийского пояса). В таких сообществах явление доминирования выражено очень сильно. Геометрическая последовательность может быть близка также к ряду значимости видов определенного яруса растительного сообщества, хотя этот ярус и не представляет собой всего сообщества. Геометрический ряд, помимо того может выражать исход конкуренции между ограниченным числом видов, зависящих от одних и тех же ресурсов среды.

Модель «разломанного стержня» Р. Мак-Артура. Мо-

дель разломанного стержня (кривая II) основывается на гипотезе случайных границ между экологическими нишами. Ниши видов в сообществе не перекрываются, но тесно прилегают друг к другу. При этом число особей каждого вида пропорционально размеру (ширине) ниши. Эта модель рассматривает только один ресурс. Она отражает более равномерное его разделение, чем геометрическая модель. Модель «разломанного стержня» характеризуется только одним параметром S (числом видов) и сильно зависит от объема выборки.

Значимость вида k в ряду от i = 1 (наименее значимый вид) до i = M (наиболее значимый вид) определяется по формуле:

где N = n(i) – сумма значимостей всех видов; M – число видов в сообществе.

В распределении, описываемом моделью «разломанного стержня», обилия видов распределены с максимально возможной в природе равномерностью. Такое распределение

149

характерно для сообществ с интенсивной межвидовой конкуренцией, территориальным поведением, например, для лесных птиц, характер распределения которых соответствует представлению о неперекрывающихся случайных нишах. Лучше всего использовать модель «разломанного стержня» для доказательства большей выравненности обилий видов в определенном сообществе.

Логнормальное распределение. Логнормальное распре-

деление описывает ситуацию, когда ниши многомерны и перекрываются. На рисунке 11.1 логнормальное распределение представлено сигмоидальной кривой, занимающей промежуточное положение между моделью геометрического ряда и «разломанного стержня» и имеющей более крутое падение по сравнению с моделью «разломанного стержня».

Эта модель впервые была применена к распределению обилий видов Престоном. Престон нанес на ось обилия видов в логарифмическом масштабе и назвал получившиеся классы октавами. Их границам приданы удваивающиеся оценки значимости при переходе от одной октавы к следующей. На графике распределения частот видов по полученным таким способом классам численности соответствуют известной кривой нормального распределения, усеченной слева, в области частот редких видов.

Распределение обычно записывается в форме:

где NR – число видов в октаве, удаленной на R октав от модального интервала, содержащего N0 видов;

а 0,2 – постоянная, связанная со стандартным отклонением данного распределения.

Логнормальная кривая соответствует распределению значимости в многовидовых сообществах в гомогенных учетах и отображает наиболее широко распространенную в

150