belyuchenko_i_s_smagin_a_v_i_dr_analiz_dannykh_i_matematiche

Таблица16.4 – Рацион хищника

Постановка задачи.

1.В качестве показателя эффективности целесообразно взять энергетические затраты хищника.

2.В качестве управляемых переменных задачи следует

взять:

x1 – количество жертв I вида, отлавливаемого хищником;

x2 – количество жертв II вида, отлавливаемого хищником.

3.Целевая функция:

F = 3x1 + 2x2 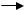min,

где 3 – энергетические затраты хищника на поимку жертвы вида I; 2 – энергетические затраты хищника на поимку жертвы вида II.

4. Ограничения по составу необходимых питательных веществ в рационе хищника:

5x1 + 1x2 ≥ 10,

2x1 + 2x2 ≥ 12,

1x1 + 4x2 ≥ 12.

5. Ограничения по области определения:x1 0, x2 0. Решение ( рисунок 16.1).

На первом шаге следует определить все возможные неотрицательные значения переменных x1 и x2, которые удовлетворяют ограничениям. С этой целью в декартовой системе координат наносим линии, соответствующие уравнениям прямых:

5x1 + 1x2 = 10;

261

2x1 + 2x2 = 12;

1x1 + 4x2 = 12; x1 = 0, x2 = 0.

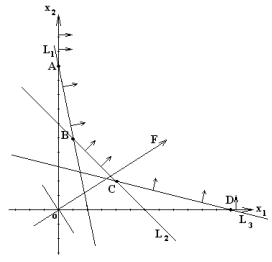
Рисунок 16.1 – Графический метод решения задачи о рационе хищника

Строить их проще всего по двум точкам. Например, построим первую линию. Пусть х1 = 0, тогда х2 = 10. Если взять х1 = 1,то х2 получится 5. Дальше через эти две точки можно по линейке провести прямую линию. Аналогично строим все остальные линии. Не забываем, что уравнение оси абсцисс:x2 = 0, а оси ординат:x1 = 0.

Дальше заштриховываем область, в точках которой выполняются все ограничения. Каждая такая точка называется допустимым решением, а множество всех допустимых решений называется допустимой областью. Очевидно, что решение задачи ЛП состоит в отыскании наилучшего решения в допустимой области, которое, в свою очередь, называ-

ется оптимальным.

262

В рассматриваемом примере оптимальное решение представляет собой допустимое решение, минимизирующее

функцию F = 3x1 + 2x2.

Значение целевой функции, соответствующее оптимальному решению, называется оптимальным значением задачи ЛП. В нашем случае, для нахождения оптимального решения проводим через начало координат радиус-вектор целевой функции, он имеет координаты (3;2). Затем строим линию уровня, перпендикулярную радиус-вектору. Путем параллельного переноса полученной прямой находим вершины, в которых происходит только касание с допустимой областью. В рассматриваемой задаче многоугольник решений представляет собой неограниченную область, а точкой входа в область является точка В. Ее координаты находим, решая систему уравнений:

5x1 + 1x2 = 10,

2x1 + 2x2 = 12, х1 = 1; х2 = 5;

Таким образом, рацион, удовлетворяющий пищевые потребности хищника при наименьших затратах энергии, означает ежедневное потребление в среднем одной жертвы вида I и пяти жертв вида II. Энергетические затраты хищника при этом составят 3x1 + 2x2 = 3∙1+2∙5 = 13 ед. энергии. Специализируясь только на одном виде жертвы, хищник смог бы удовлетворить свои потребности, но лишь при существенно большем потреблении и более высоких затратах энергии.

263

16.8 Алгоритм решения задачи линейного программирования графическим способом

1.Обозначим неизвестные.

2.Составим систему ограничений и целевую функцию.

3.Запишем уравнения граничных прямых и построим их графики.

4.Определим область допустимых решений системы ограничений задачи.

5.Приравняем целевую функцию нулю и строим ради- ус-вектор

F ( dF ; dF ) . dx1 dx2

Координатами вектора F являются координаты целевой функции.

6. Проводим линию уровня, которая перпендикулярна

F .

7.Линию уровня перемещаем по направлению вектора F для задач на максимум и в направлении, противоположном F для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у нее не окажется одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задач ЛП, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон области допустимых решений, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача будет иметь бесчисленное множество решений.

16.9 Алгоритм симплексного метода

Графический метод ввиду большой размерности реальных практических задач ЛП достаточно редко применяется,

264

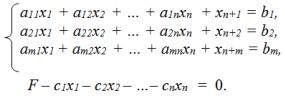
однако он позволяет ясно уяснить одно из основных свойств ЛП – если в задаче ЛП существует оптимальное решение, то оно находится, по крайней мере, в одной из вершин до-

пустимой области. Несмотря на то, что допустимая область задачи ЛП состоит из бесконечного числа точек, оптимальное решение всегда можно найти путем целенаправленного перебора конечного числа ее вершин.

Рассматриваемый симплекс-метод решения задачи ЛП основывается на этом фундаментальном свойстве.

Практические расчеты при решении реальных задач симплексным методом выполняется в настоящее время с помощью компьютеров. Если расчеты осуществлять вручную, то удобно использовать так называемые симплексные таблицы. Далее мы рассмотрим алгоритм их составления, не углубляясь в его подробное обоснование. Для определенности считаем, что решается задача на отыскание максимума.

1. После введения добавочных переменных систему уравнений и линейную функцию записываем в виде, кото-

рый называется расширенной системой:

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены; в противном случае используем так называемый М-метод.

2. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком: bi = – сi. В ле-

265

вом столбце таблицы записываем основные переменные (базис), в первой строке таблицы – все переменные (отмечая при этом основные), во втором столбце – свободные члены расширенной системы b1, b2, ..., bm. Последний столбец подготовлен для оценочных отношений, необходимых при расчете возможного наибольшего значения переменной. В рабочую часть таблицы (начиная с третьего столбца и второй строки) занесены коэффициенты аij при переменных из расширенной системы. Далее таблица преобразуется по определенным правилам.

3.Проверяем выполнение критерия оптимальности при решении задачи на максимум – наличие в последней строке

отрицательных коэффициентов b i< 0 (с i> 0). Если таких нет, то решение оптимально, достигнут max F = с0 (в левом нижнем углу таблицы), основные переменные принимают

значения аi0 (второй столбец), т. е. получаем оптимальное базисное решение.

4.Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент bi <0 в последней строке определяет разрешающий столбец s.

Составляем оценочные ограничения каждой строки по следующим правилам:

1) ∞, если bi и ais имеют разные знаки;

2)∞, если bi = 0 и ais < 0;

3)∞, если ais = 0;

4)0, если bi = 0 и ais > 0;

5)bi , если аi0 и ais имеют одинаковые знаки.

ais

Определяем min bi . Если конечного минимума нет,

ais

то задача не имеет конечного оптимума (Fmin = ∞). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разре-

266

шающей строкой. На пересечении разрешающей строки и столбца находится разрешающий элемент аis.

5. Переходим к следующей таблице по правилам:

а) в левом столбце записываем новый базис: вместо основной переменной хq – переменную xs;

б) новую строку с номером q получаем из старой делением на разрешающий элемент аqs;

в) расставляем нули и единицы:

–в новой таблице в столбце, соответствующем разрешающему столбцу предыдущей таблицы на месте разрешающего элемента – «1», остальные – «0»;

–если в начальной строке новой таблицы имеются коэффициенты, равные «0», то соответствующие им столбцы переписываются без изменения;

–если в разрешающем столбце симплексной таблицы имеются коэффициенты, равные «0», то соответствующие строки в новой таблице переписываются без изменения;

–остальные элементы таблицы вычисляются по правилу треугольника:

Далее переходим к пункту 3 алгоритма.

16.10 Пример решения задачи симплекс-методом

Задача об использовании ресурсов. Для изготовления двух видов продукции Р1 и Р2 используют четыре вида ресурсов S1, S2, S3, и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 16.5.

267

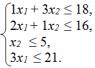
Таблица 16.5 – Справочная таблица для задачи о ресурсах

Прибыль, получаемая от единицы продукции Р1 и Р2 – соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от реализации будет максимальной. Такая постановка задачи часто применяется в экономике. Но ограничения на ресурсы могут быть вызваны и экологическими соображениями.

Постановка задачи.

Обозначим через х1 и х2 – число единиц продукции соответственно Р1 и Р2, запланированных к производству. Для их изготовления потребуется (1х1 + 3х2) единиц ресурса S1, (2х1 + 1х2) единиц ресурса S2, (1х2) единиц ресурса S3, и 3х1 единиц ресурса S4. Так как потребление ресурсов S1, S2 S3, и S4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

(16.13)

По смыслу задачи переменные

268

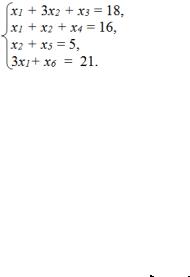
Суммарная прибыль F от реализации продукции Р1 составит 2х1 руб. и от реализации продукции Р2: 3х2 руб., т. е.

Итак, математическая модель задачи: найти такой план выпуска продукции Х = (х1, х2), удовлетворяющий системе 16.13 и условию 16.14, при котором функция 16.15 принимает максимальное значение.

Расширенная система имеет вид:

Линейную функцию представим в виде:

F – 2х1 – 3х2 = 0.

Заполняем первую симплексную таблицу (таблица16.6), в которой переменные х3, х4, х5, х6 основные. Последняя строка заполняется коэффициентами линейной функции с противоположным знаком (см. п. 2 алгоритма).

Таблица 16.6 – Первая симплексная таблица

В соответствии с п. 3 алгоритма проверяем критерий оптимальности.

269

Впоследней строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (–3); вто-

рой столбец разрешающий, переменная х2 перейдет в основные (этот столбец отмечен стрелкой).

Всоответствии с п. 4 находим оценочные отношения

х2 = min {l8/3; 16; 5; ∞} = 5.

Третья строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит разрешающий элемент а33 = 1.

Строим таблица 5.2 по правилам п. 5 алгоритма:

а) в новом базисе основные переменные: х3, х4, х2, х6; б) расставляем нули и единицы;

В последней строке против всех основных переменных ставим 0. Третья строка получается делением на разрешаю-

Критерий оптимальности вновь не выполнен. Теперь первый столбец разрешающий; х1 – переходит в основные, min{3/1; 11/2; ∞; 7} = 3; первая строка разрешающая; а11

– разрешающий элемент.

Новая симплексная таблица примет вид таблицы 16.8.

270