
belyuchenko_i_s_smagin_a_v_i_dr_analiz_dannykh_i_matematiche
.pdfособей от каждой группы погибает. Потомство, которое появилось за единицу времени от всех групп, поступает в группу 1. Тогда первая компонента вектора X(t) имеет вид:
k p
x1 (t1 ) ai xi (t0 ) ak xk (t0 ) ak 1 xk 1 (t0 ) ak p xk p (t0 ) (14.3)
i k
Вторая компонента получается с учетом двух процессов. Первый – переход особей, находившихся в момент t0 в первой группе, во вторую. Второй процесс – возможная гибель части из этих особей. Поэтому вторая компонента x2 (t1) равна не всей численности x1(t0), а только некоторой ее части
β1x1(t0), 0< βn<1 |
(14.4) |
Аналогично получаются третья компонента β2x2(t0)и все остальные.
Предположим, что все особи, находившиеся в момент t0 в последней возрастной группе к моменту t1 погибнут. Поэтому последняя компонента вектора X (t1) составляется лишь из тех особей, которые перешли из предыдущей возрастной группы.
Xn(tn) = n-1 Xn-1(tn), |
0<βn<1 |
(14.5) |
Коэффициенты для каждой группы имеют следующий смысл:
α – коэффициент рождаемости; β – коэффициент выживания.
Вектор численностей возрастных групп в момент времени t1 представим в виде:
211
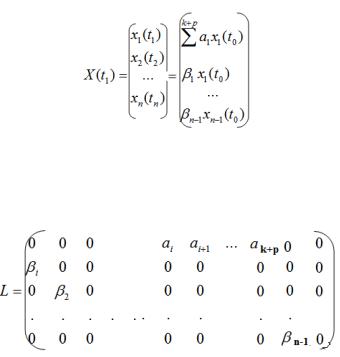
(14.5)
Вектор X(t1) получается умножением вектора X(t0) на матрицу перехода:
(14.6)
Структура матрицы перехода: по диагонали матрицы стоят нули, под диагональными элементами коэффициенты выживания β; на первой строке стоят члены, характеризующие число особей, родившихся от соответствующих групп (коэффициенты рождаемости) α; все остальные элементы матрицы равны нулю.
Зная структуру матрицы L и начальное состояние популяции – вектор-столбец X(t0), – можно прогнозировать состояние популяции в любой наперед заданный момент времени.
Для этого необходимо каждый раз умножать вектор состояния популяции на матрицу Лесли.
X (t1 ) L X (t0 ), |
(14.7) |
212

X (t2 ) L X (t1 ) L L X (t0 ) L2 X (t0 ),
X (tk ) L X (tk 1 ) Lk X (t0 )
Главное собственное число матрицы L дает скорость, с которой размножается популяция, когда ее возрастная структура стабилизировалась.
14.2Пример матричной модели популяции из трех возрастных групп
Пусть возрастная динамика популяции характеризуется матрицей:
(14.8)
Такая запись означает, что исходная популяция состоит из одной самки старшего возраста (вектор столбец в правой части уравнения). Каждое животное старшего возраста, прежде чем умереть, успевает произвести в среднем 12 потомков, каждое животное среднего возраста, прежде чем умереть или перейти в следующий возрастной класс (вероятности этих событий одинаковы) производит в среднем 9 потомков. Молодые животные не производят потомства и с вероятностью 1/3 попадают в среднюю возрастную группу. По прошествии одного временного интервала в популяции будет уже 12 самок младшего возраста:
(14.9)
213
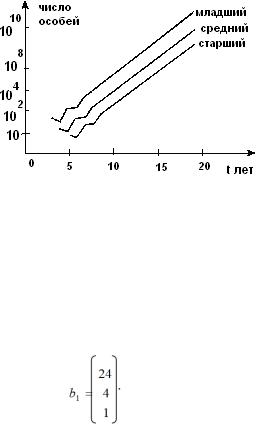
Далее процедуру следует повторять на каждом шаге. Из графика (Рисунок 14.1) видно, что до некоторого момента времени ( t10), наблюдаются колебания численности, после чего количество самок всех трех возрастов экспоненциально возрастает, причем соотношение между ними остается постоянным. Главное собственное число 1 при этом рав-
но 2, т. е. размер популяции за каждый временной шаг удваивается.
Рисунок 14.1 – Численность самок старшего, среднего и младшего возраста в зависимости от времени для первых 20 временных интервалов (Джефферс, 1981)
Наклон графика равен ln 1 – собственной скорости ес-
тественного прироста. Соответствующий главному собственному числу собственный вектор отражает устойчивую структуру популяции и в нашем случае равен:
(14.10)
214
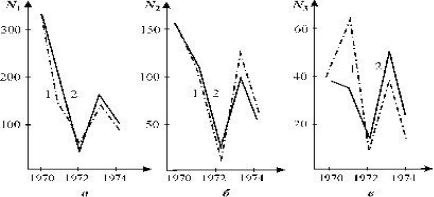
Этот пример страдает тем же недостатком, что и модель Мальтуса экспоненциального роста: мы допускаем, что популяция может неограниченно расти. Более реалистическая модель должна учитывать, что все элементы матрицы L являются некоторыми функциями размера популяции.
Рисунок 14.2 – Динамика численности ценопопуляции овсеца Htlictotrichon S. Для различных возрастных групп; а – проростки, прегенеративные и генеративные особи, б - субсенильные особи,
в - сенильные особи. 1 – эмпирические данные, 2 – прогноз по модели Лесли. (Розенберг, 1984)
Модели с применениями матриц Лесли для крупных возрастных групп могут дать описание колебательных изменений численности популяции. В качестве примеров использования модели П. Лесли можно привести в фитоценологии описание возрастной структуры сосны (Pinus sylvestris) в Шотландии (Usher, 1969, 1972) и описание возрастной структуры ценопопуляции овсеца Шелля – мелкодерновинного злака северных луговых степей (Розенберг,
1984) (Helicto-trichon schellianum; Розенберг, 1982) (Рисунок
14.2). Эта модель позволила описать наблюдаемые в приро-
215
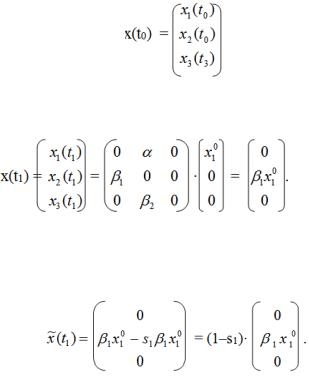
де явления – старение овсеца и колебания распределений по возрастному спектру в течение ряда лет.
14.3Управление эксплуатацией популяции на основе матричной модели
Рассмотрим несколько модельных ситуаций управления тактикой рыбного промысла на основе матричной модели Лесли.
Пусть популяция представляет собой три возрастные группы и в начальный момент времени имеются только особи 1-ой возрастной группы.
(14.11)
Тогда в следующий момент времени будет
(14.12)
Отловим часть имеющихся особей s1x2(t1); 0 s1 1.После улова имеем вектор:
(14.13)
216

В следующий момент времени t2 имеем:
(14.14)
Пусть s2x3(t2) отлов пострепродуктивной группы. Тогда после отлова будем иметь:
(14.15)
В общей сложности после двух тактов отлова величина отлова составит s s1x2 (t1 ) s2 x3 (t1 ) и популяция придет в
состояние ~ . x (t2 )
1) Изъятие части популяции с возвращением в исходное состояние.
Подобрать коэффициенты s1 и s2 таким образом, чтобы популяция вернулась в исходное состояние, и рассчитать количество улова.
Решение.
Такое условие будет выполняться при условии, что
~ = x(t0). x (t2 )
217
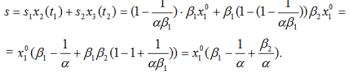
Приравняем компоненты этих векторов.
(1 s ) x0 x0 , |
(14.16) |
||||
1 |
1 |
1 |
1 |
||
|
|||||
1 (1 s1 ) 2 (1 s2 )x10 0
Из первого уравнения, сокращая х1 находим s1:
1 s1 |
x10 |
|
|
1 |
; |
(14.17) |
||
x0 |
|
|
||||||
|
1 |
1 |
|
|
1 |
|
|
|
s1 |
1 |
1 . |
|
|
||||
1 |
|
|
||||||
|
|
|
|
|||||
Второе уравнение выполняется, когда s2 = 1, т. е. вылавливается вся пострепродуктивная группа.
Итак, в первоначальное состояние популяция вернется при выполнении условий:
s 1 |
1 |
и s2 = 1. |
(14.18) |
1 |
1 |
|
|
|
|
|
Улов рассчитаем по формуле:
(14.19)
Пример. Дана популяция речного карпа с тремя возрастными группами, у которой в начальный момент времени имеется 100 особей только 1-ой возрастной группы. Коэффициент выживаемости 1-ой возрастной группы равен 0,8; 2-ой возрастной группы – 0,7. Коэффициент рождаемости репродуктивной группы равен 3. Найти, какую часть особей необходимо вылавливать, чтобы после двух сезонов попу-
218

ляция пришла в исходное состояние. Рассчитать количество улова.
Решение. В нашей задаче имеем β1 = 0,8; β2 = 0,7; α = 3;
x0 = 100
Воспользуемся готовыми формулами (14.17–14.19):
|
s1 1 |
1 |
1 |
|
1 |
|
0,58; |
|||||||
|
|
|
|
|||||||||||
|
1 |
0,8 3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
s x0 |
( |
1 |
|
2 ) 100 (0,8 |
1 |
|
0,7 |
) 70 . |
||||||
|
|
|
||||||||||||
1 |
1 |
|
|
|
|
|
|
3 |
3 |
|
||||
|
|
|
|
|
|
|
||||||||
2) Изъятие популяции с сохранением определенной части предрепродуктивной группы
Найти оптимальный режим отлова такой, чтобы величина отлова s была максимальной, а численность молодняка была бы не ниже некоторого числа m1.
Формально это условие можно записать следующим образом:
max s max[ s1x2 (t1 ) s2 x3 |
(t2 )], |
|||
~ |
|
, |
|
(14.20) |
x1 (t2 ) m1 |
|
|
||
(1 s ) x0 |
m . |
|
||
1 |
1 |
1 |
1 |
|
Из первого выражения видно, что max s max s1 max s2. Понятно, что max s2 = 1.
s1 найдем из неравенства 1 (1 s1 ) x10 m1 . Выразим отсюда сначала (1 – s1), а затем s1.
1 s1 |
m1 |
|
; |
x0 |
|||
|
1 |
1 |
|
s1 1 |
m1 |
|
. |
x0 |
|||
|
1 |
1 |
|
Понятно, что максимальное значение достигается при
s1 1 |
m1 |
|
|
(14.21) |
|
x0 . |
|||||
|
|||||
|
1 |
1 |
|
|
|
219

Пример. По данным предыдущей задачи рассчитать режим отлова такой, чтобы улов был максимальный, а количество молодняка было не ниже 50.
Решение. Воспользуемся готовой формулой (14.21):
s 1 |
m1 |
|
1 |
50 |
1 |
|
1 |
1 |
0,208 |
0,8 . |
|
|
|
|
|||||||
1 |
x0 |
|
0,8 3 100 |
|
|
4,8 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
1 |
|
|
|
|
|
|
|
|
3) Изъятия популяции с сохранением определенных частей предрепродуктивной и пострепродуктивной групп
Найти максимальное s при условии, что
1) численность молодняка была бы не ниже некоторого
уровня m1.
2) численность пострепродуктивной группы была бы не ниже некоторого уровня m2.
Формально это условие записывается следующим образом:
max s max[ s1 x2 (t1 ) s2 x3 (t2 )], |
|
|
~ |
(t2 ) m1 , |
(14.22) |
x1 |
||
~ |
(t2 ) m2 . |
|
x3 |
|
|
Максимальное значение s будет достигнуто при максимальном значении s1 и максимальном значении s2.
Из предыдущей задачи максимум |
s1 1 |
m1 |
|
. |
x0 |
||||
|
|
1 |
1 |
|
s2 найдем, решая неравенство:
1 (1 s2 ) 2 (1 s1 ) x10 m2 ;
1 s2 |
|
|
|
m2 |
|
|
; |
|
|
1 |
(1 s ) |
2 |
x0 |
||||
|
|
|
||||||
|
|
|
1 |
1 |
|
s2 1 m2 0 .
1 (1 s1 ) 2 x1
Максимум достигается при равенстве, т. е.
220
