Множественная регрессия и корреляция Методические указания

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

у=f(x1, x2, … xp),

(2.1)

где:

у – зависимая переменная (результативный признак);

x₁, x₂, … x_p – н езависимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используют сле-дующие функции:

• линейная

  y=a+b1∙x1+b2∙x2+…+bp∙xp+;

  (2.2)

• степенная

  y=a∙ ∙ ;

  (2.3)

• экспонента

  y=

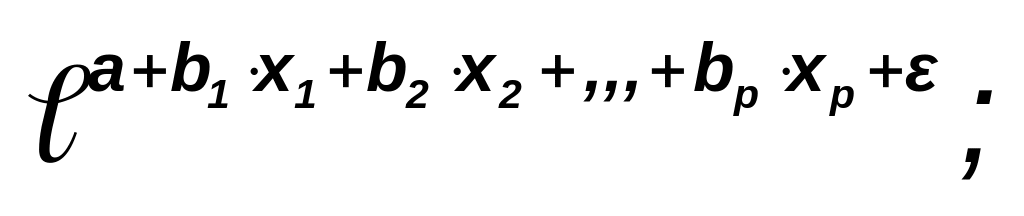
  (2.4)

• гипербола

y=

(2.5)

Можно использовать и другие функции, приводимые к линейному виду.

Для оценки параметров уравнения множественной регрессии применяют ме-тод наименьших квадратов (МНК). Для линейных уравнений и нелинейных урав-нений, приводимых к линейным, строится следующая система нормальных урав-нений, решение которой позволяет получить оценки параметров регрессии:

(2.6)

Для ее решения может быть применен метод определителей:

где:

– определитель системы;

– частные определители; которые получаются путем за-мены соответствующего столбца матрицы определите-ля системы данными левой части системы;

Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:

(2.7)

где:

– стандартизованные переменные;

– стандартизованные коэффициенты регрессии.

К уравнению множественной регрессии в стандартизованном масштабе при-меним МНК. Стандартизованные коэффициенты регрессии ( -коэффициенты) определяются из следующей системы уравнений:

(2.8)

Связь коэффициентов множественной регрессии b_i со стандартизованными коэффициентами описывается соотношением

(2.9)

Параметр а определяется как

(2.10)

Средние коэффициенты эластичности для линейной регрессии рассчитыва-ются по формуле

(2.11)

Для расчета частных коэффициентов эластичности применяется следую-щая формула:

(2.12)

Тесноту совместного влияния факторов на результат оценивает индекс мно-жественной корреляции:

(2.13)

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

(2.14)

Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде

(2.15)

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

(2.16)

где:

– определитель матрицы парных ко-эффициентов корреляции;

– определитель матрицы межфакторной корреляции.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_і при неизменном уровне других факторов, можно определить по фор-муле

(2.17)

или по рекуррентной формуле:

(2.18)

Частные коэффициенты изменяются в пределах от –1 до 1.

Качество построенной модели в целом оценивает коэффициент (индекс) де-терминации. Коэффициент множественной детерминации расчитывается как квадрат индекса множественной корреляции:

Скорректированный индекс множественной детерминации содержит по-правку на число степеней свободы и рассчитывается по формуле

(2.19)

где:

n – число наблюдений;

т – число факторов.

Значимость уравнения множественной регрессии в целом оценивается с по-мощью F-критерия Фишера:

(2.20)

Частный F-критерий оценивает статистическую значимость присутствия каж-дого из факторов в уравнении. В общем виде для фактора х_і частный F-критерий определится как

(2.21)

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения

(2.22)

где:

= средняя квадратическая ошибка коэффициента регрессии b_i, которая может быть определена по следующей формуле:

(2.23)

При построении уравнения множественной регрессии может возникнуть проб-лема мультиколлинеарности факторов, их тесной линейной связанности.

Считается, что две переменные явно коллинеарны, т.е. находятся между со-бой в линейной зависимости, если

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности фак-торов. Чем сильне мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с по-мощью метода наименьших квадратов.

Для оценки мультиколлинеарности факторов может использоваться опреде-литель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэф-фициентов корреляции между факторами была бы единичной матрицей, посколь-ку все недиагональные элементы были бы равны нулю. Так, для включающего три объясняющих переменных уравнения

(2.24)

матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:

(2.25)

так как

Если же, наоборот, между факторов существует полная линейная зависи-мость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

(2.26)

Чем ближе к 0 определитель матрицы межфакторной корреляции, тем силь-нее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной кор-реляции, тем меньше мультиколлинеарность факторов.

Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Доказано, что величина

(2.27)

имеет приближенное распределение степенями свободы. Если фактическое значение превосходит табличное (критическое) то гипотеза Н₀ отклоняется. Это означает, что недиа-гональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Для применения МНК требуется, чтобы дисперсия остатков была гомоскедас-тичной. Это значит, что для каждого значения фактора x_j остатки имеют оди-наковую дисперсию. Если это условие не соблюдается, то имеет место гетеро-скедостичность.

При нарушении гомоскедастичности мы имеем неравенства

.

При малом объеме выборки для оценки гетероскедастичности может исполь-зоваться метод Гольдфельда-Кванта. Основная идея теста Гольдфельда-Кванта состоит в следующем:

1) упорядочение п наблюдений по мере возрастания переменной х;

2) исключение из рассмотрения С центральных наблюдений; при этом (п-С):2>р, где р – число оцениваемых параметров;

3) разделение совокупности из (п-С) наблюдений на две группы (соответст-венно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии;

4) определение остаточной суммы квадратов для первой (S₁) и второй (S₂) групп и нахождение их отношения: R=S₁:S₂.

При выполнении нулевой гипотезы о гомоскедастичности отношения R будет удовлетворять F-критерию со степенями свободы ((п – С – 2р):2) для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем больше нарушена предпосылка о равенстве диспер-сий остаточных величин.

Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т.д.). Чтобы ввести такие перемен-ные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т.е. качественные переменные преобразовать в количественные. Такого вида сконструированные переменные принято в эконометрии называть фиктивными переменными. Например, включать в модель фактор «пол» в виде фиктивной переменной можно в следующем виде:

(2.28)

Коэффициент регрессии при фиктивной переменной интерпретирует как сред-нее изменение зависимой переменной при переходе от одной категории (женский пол) к другой (мужской пол) при неизменных значениях остальных параметров. На основе t-критерия Стьюдента делается вывод о значимости влияния фиктив-ной переменной, существенности расхождений между категориями.