Прогнозирование при наличии сезонной компоненты

По временным рядам за ряд лет в помесячном или поквортальном разрезе могут наблюдаться сезонные колебания.

Сезонные колебания – это разновидность периодических колебаний. Для них характерны внутригодичные, повторяющиеся устойчиво из месяца в месяц (из квартала в квартал) изменения в уровнях. Иными словами, сезонные колебания – регулярно повторяющиеся подъемы и снижения уровней динамического ряда внутри года на протяжении ряда лет. Сезонность имеет место в самых различных областях экономики. Погодные изменения влияют на ассортимент реализации обуви (зимняя, весенне-осенняя, летняя), овощей и многих других товаров. В строительстве наибольшее оживление деятельности проявляется летом; в этот же период времени года наблюдается максимальный наплыв туристов. Наобо-рот, театры Москвы, Санкт-Петербурга хотя и работают летом, но в значительной мере по сокращенной программе, предоставляя в основном свое помещение для театральных коллективов других городов. Сезонность может проявляться не только к месячным, но и к дневным, недельным данным. Так, кафе, рестораны, театры часто испытывают подъем спроса в конце недели.

Существуют две различные модели сезонности: аддитивная и мультиплика-тивная.

В аддитивной модели сезонность выражается в виде абсолютной величины (например, 5 т), которая добавляется или вычитывается из среднего значения ря-да, чтобы выделить показатель сезонности. В мультипликативной модели се-зонность выражена как процент от среднего уровня (например, 120%), который должен быть учтен при прогнозировании путем умножения на него среднего зна-чения ряда.

Методика построения аддитивной и мультипликативной модели различается в зависимости от того, есть или нет тенденция в ряду динамики.

Если в ряду динамики отсутствует тенденция, то уровень временного ряда рассматривается как функция сезонности и случайности:

y_i=f(S,ε),

где:

y_i – фактические уровни динамического ряда;

S – сезонная составляющая;

ε – случайная компонента.

Графически такой ряд может быть представлен рис. 8.

При аддитивной модели уровни такого ряда можно представить следующим образом:

Рис. 8 – Временной ряд с сезонной и случайной составляющей

Тогда общий уровень колебаний динамического ряда раскладывается на две составляющие: S – влияние сезонности, ε – влияние случайности.

Тогда:

где:

– средний уровень ряда соответствующего периода внутри года (месяца, квартала) за ряд лет.

Величина отражает влияние сезонности (сезонная составляющая S), а величина характеризует влияние случайной компоненты (если бы его не было, то уровни динамического ряда на рис. 8 представляли бы собой плав-ную, а не ломаную линию).

При мультипликативной модели уровень динамического ряда можно предста-вить как произведение его составляющих:

где отношение представляет собой коэффициент сезонности (K_S), а – отражает влияние случайного фактора.

Чем больше коэффициент сезонности, тем больше амплитуда колебаний уровней ряда относительно его среднего уровня, тем существеннее влияние се-зонности. Чем меньше влияние случайной составляющей, тем в большей мере рассматриваемая модель адекватно описывает исходный временной ряд. Как ви-дим, отличие аддитивной модели от мультипликативной состоит в том, что в ад-дитивной модели сезонная и случайная составляющие определены в виде сла-гаемых абсолютных величин (как разности), а в мультипликативной модели – в виде сомножителей (как коэффициенты).

Прогнозирование динамического ряда с сезонными колебаниями при отсутст-вии в нем тенденции сводится к прогнозированию среднего уровня с после-дующей корректировкой его на сезонную компоненту («±» - при аддитивной моде-ли и умножение на коэффициент сезонности – при мультипликативной модели):

– аддитивная модель;

– мультипликативная модель.

Пример. Реализация детских велосипедов по магазину характеризуется сле-дующими данными (табл. 3.5).

Таблица 3.5

Кварталы	Годы (yi)
	1-й	2-й	3-й
I	25	30	26	27	0,306	-61,25
II	125	120	130	125	1,416	36,75
III	180	160	182	174	1,972	85,75
IV	30	20	31	27	0,306	-61,25
Итого	360	330	369	88,25	4,000	0

Итоговые данные за 1-й, 2-й и 3-й годы колеблются вокруг среднего уровня, не имея четкой тенденции. Поэтому рассмотренные ранее модели уместны и к данному примеру. Чтобы использовать аддитивную или мультипликативную мо-дели, рассчитаем средний уровень реализации для каждого квартала как среднюю арифметическую простую из данных за три года, а также среднеквар-тальный уровень как среднегодовой уровень, деленный на 4, или как средне-арифметическую простую из исходных уровней ряда или средних для каждо-го квартала . Так, для І квартала . Общий сред-неквартальный уровень составит:

Если бы не было влияния сезонности, то каждый квартал реализация состав-ляла бы в среднем 88 ед. Однако под воздействием сезонности она была в I и IV кварталах существенно ниже, а во II и III – выше среднего уровня.

Измерение сезонности при аддитивной модели предполагает расчет абсолют-ных показателей сезонности: (см. табл. 3.5). Из них видно, что в III квартале реализация была на 86 ед. выше среднего уровня, а в I и IV кварталах – 61 ед. ниже среднего уровня. Измерение сезонности при мультипликативной мо-дели основано на расчете коэффициентов сезонности: (см. предпо-следнюю графу табл. 3.5). Они показывают, что в III квартале реализация была почти в 2 раза выше среднего уровня, а в I и IV кварталах – составляла лишь 30% среднеквартального уровня в 88 ед. Сумма абсолютных показателей сезон-ности за год равна нулю, а коэффициентов сезонности – 4 при квартальном раз-резе и 12 – при помесячном.

Знание сезонных изменений необходимо при планировании объема продаж. Чаще при этом используются коэффициенты сезонности. Так, при планировании на 4-й год объема продаж в 350 ед. план по кварталам составит:

I квартал – ед., столько же и в IV квартале;

II квартал – ед.;

III квартал – ед. (округлено до 172, чтобы в сумме объем продаж за год составил 350 ед.=27+124+172+27).

Значительное распространение получила ситуация, когда динамический ряд имеет тенденцию. В этом случае уровень временного ряда рассматривается как функция тенденции (t), сезонности (S) и случайности (ε). Тогда аддитивная мо-дель уровня динамического ряда (y_i) примет вид:

y_i= +S+ε,

где:

– теоретическое значение уровня ряда согласно тенеденции;

S – сезонная составляющая;

ε – случайная компонента.

Общая колеблемость уровней временного ряда раскладывается на три сос-тавляющие:

где:

y_S – тренд с учетом сезонности, т.е. уровень динамического ряда, одновре-менно обусловленный влиянием тенденции и сезонности; S=y_S– ; ε=y_i–y_S.

Графически влияние этих составляющих может быть представлено на рис. 9.

Чем больше угол наклона линии тренда ( ) к среднему значению ряда , тем бьольше влияние тенденции (рис. 9а). Чем больше плавная кривая y_S откло-няется от линии тренда ( ), тем значительнее влияние сезонности (рис. 9б). Чем ближе фактические уровни временного ряда (y_i) подходят к плавной линии точек y_S, тем меньше влияние случайности (рис. 9в).

а) б) в)

Рис. 9 – Разложение динамического ряда на составляющие

При мультипликативной модели уровень динамического ряда можно предста-вить в виде сомножителей:

,

где:

y_i – фактические уровни динамического ряда;

– теоретические значения уровней динамического ряда согласно тенден-ции;

K_S – коэффициент сезонности;

E – коэффициент влияния случайности (y_i/y_S).

Так как в мультипликативной модели сезонность выражена в процентах, то при наличии тенденции в ряду динамики амплитуда сезонности колебаний меня-ющаяся. Так, если коэфициент сезонности примет значение для І квартала 1,2, или 120% то при повышающейся тенденции в ряду динамики прирост в 10% бу-дет для І квартала каждого года представлять собой увеличивающуюся сезонную волну (см. рис. 10).

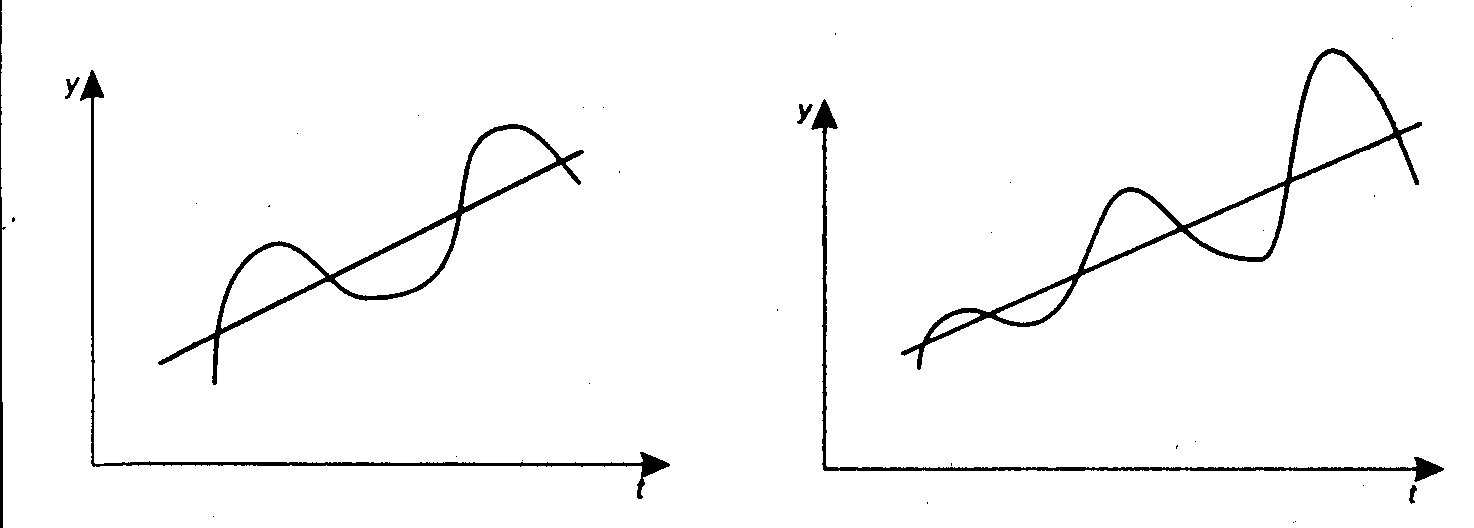
Рис. 10 – Сезонность: сравнение аддитивной и мультипликативной модели