§3. Частинні випадки множення матриць.

Нехай А=(а_ij),В=(b_ij) – квадратні матриці однакового порядку n. В такому випадку добутки АВ і ВА завжди можна утворити, причому в результаті обидві матриці також будуть квадратними n-го порядку.

Приклади.

1. Комутативні матриці:

A = B =

АВ = ВА =

2) Знайти добуток матриць:

A = 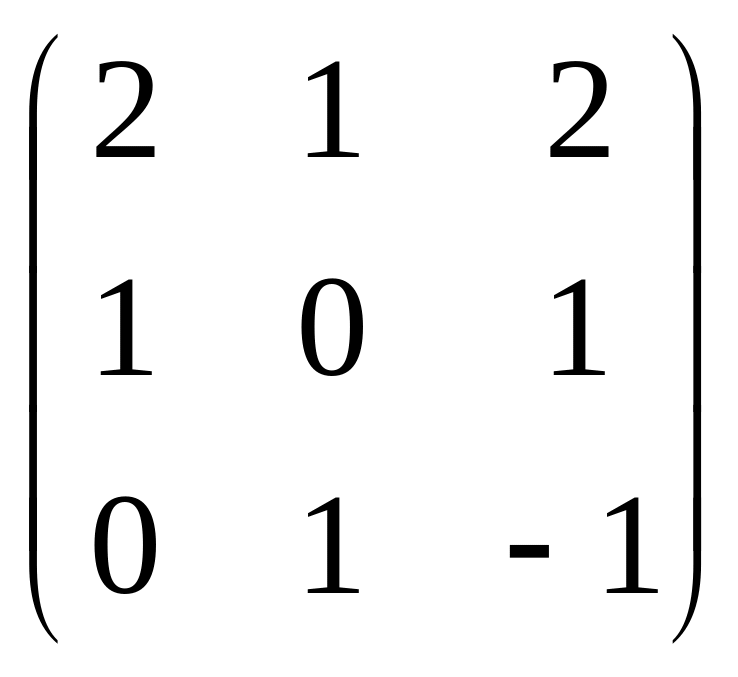B =

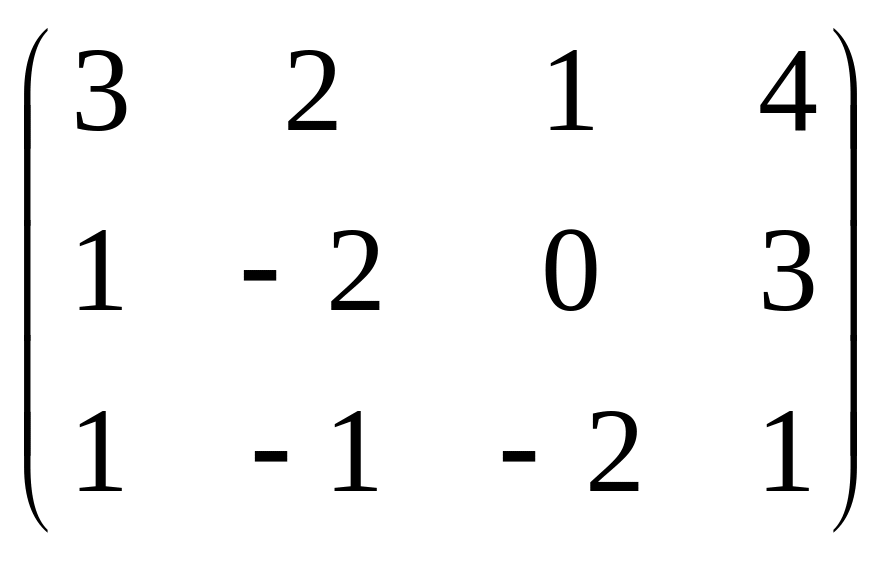
AB = =

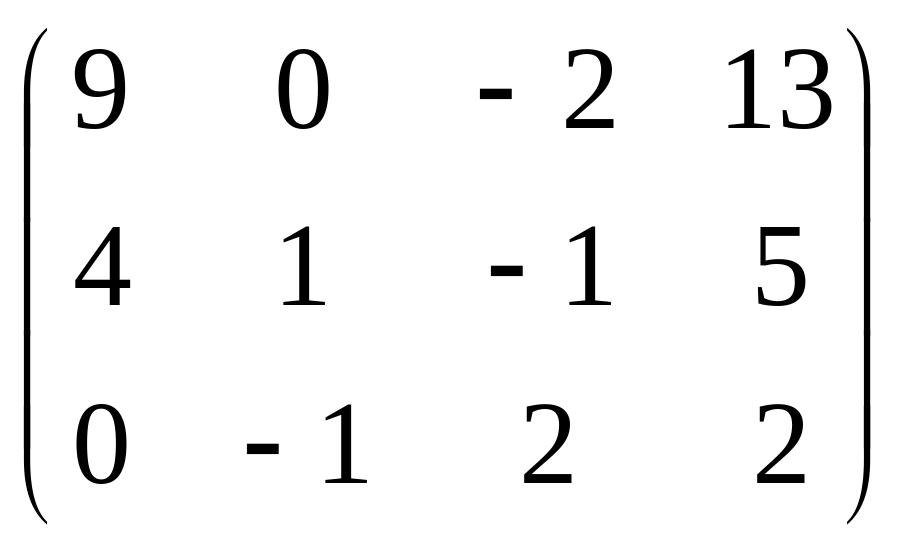
Дві відмінні від нульових матриці, добуток яких дорівнює нулю, називаються дільниками нуля.

Наприклад a) b)

3. Знайти добуток (АВ)С, якщо

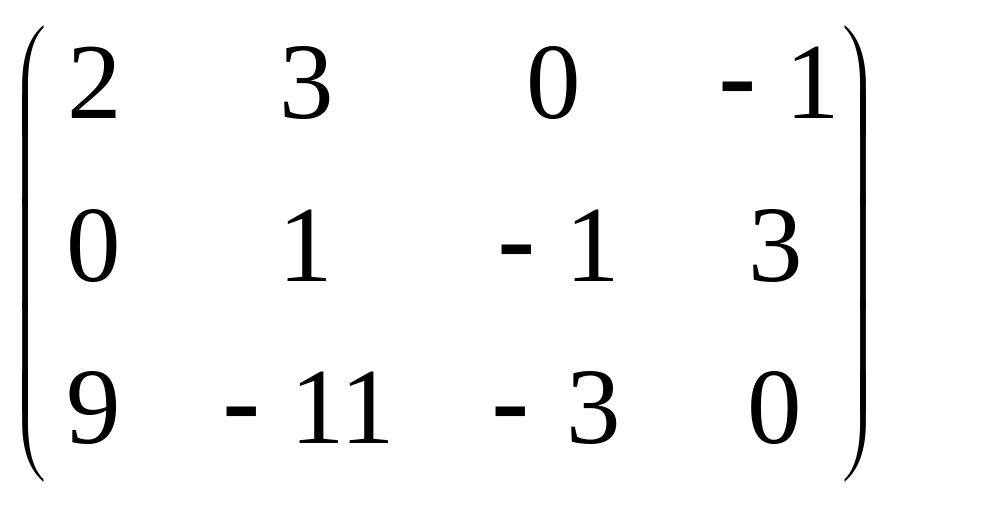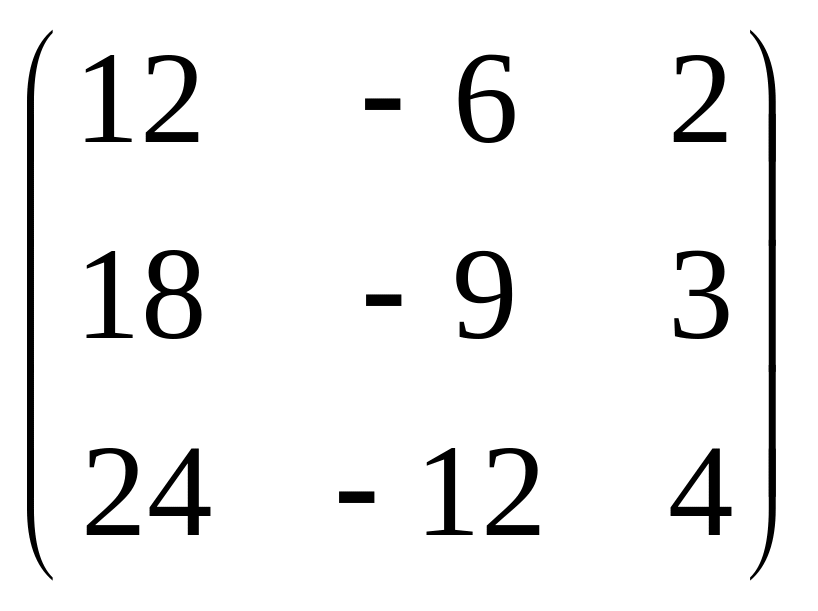A = B = C =

Добутку не існує, так як кількість стовпчиків першої матриці не дорівнює кількості рядків другої матриці.

4. Знайти всі матриці, комутативні матриці А

A =

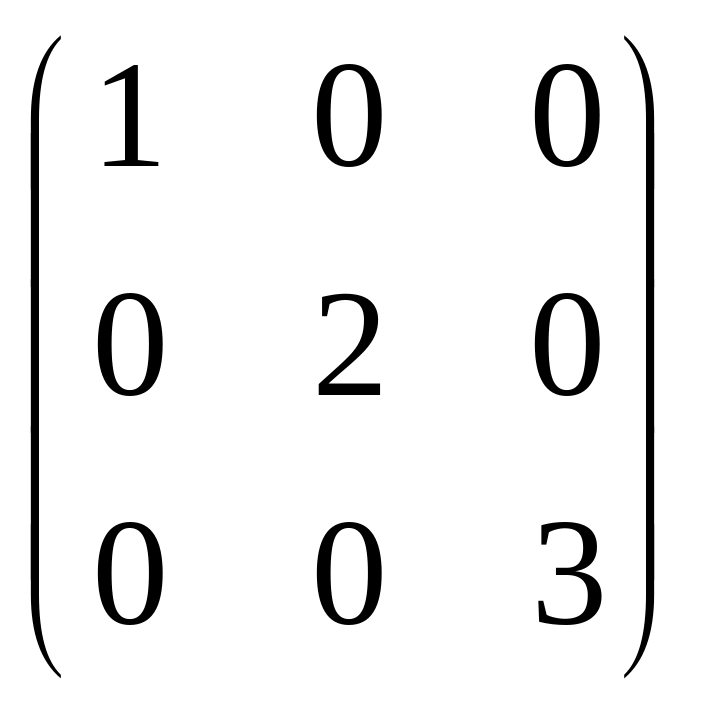
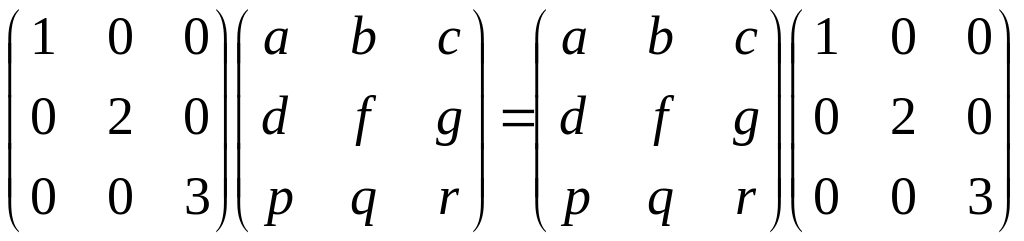
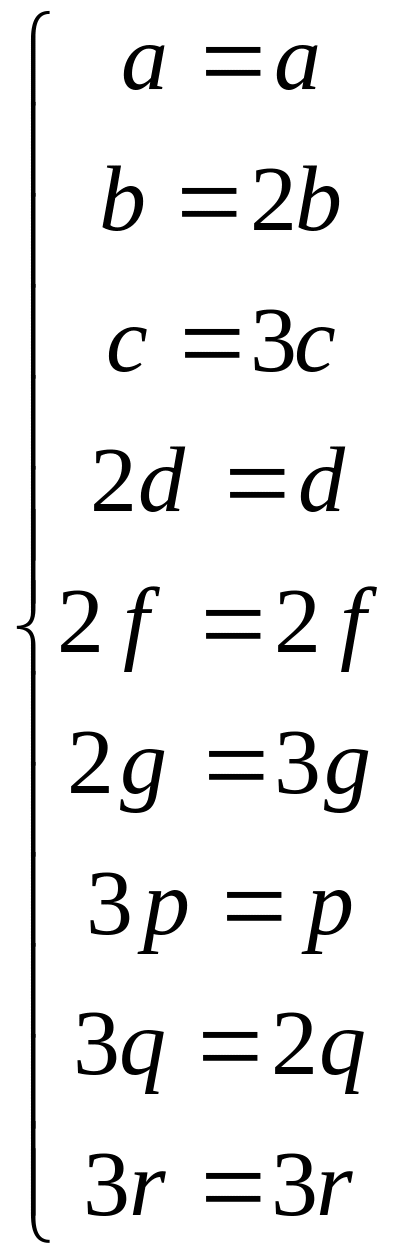=> b=c=d=g=p=q=0, a,f,r є R.

Шукана матриця

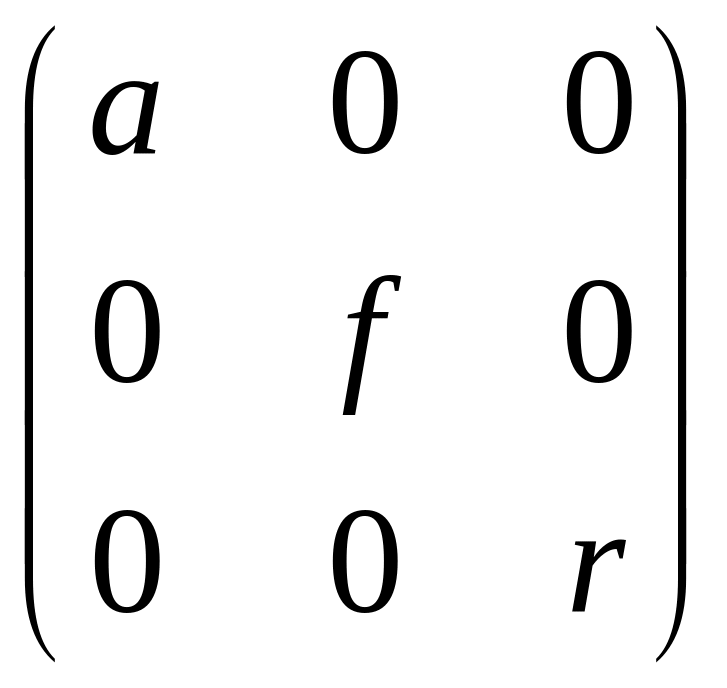
5) Обчислити

1. n=1

2. n=2

3. n=3

Доведемо методом математичної індукції =

Припустимо, що при n=k

і доведемо, що при n=k+1

Справедливість твердження при n=1 вже перевірено.

Отже, для n N.

§4. Обернена матриця.

Означення. Матрицею, оберненою до матриці А, називається матриця А^-1, яка має таку властивість

АА^-1=А^-1А=Е, де Е – одинична матриця відповідного порядку.

Матриця, для якої існує обернена їй матриця, називається оборотною.

Наслідки. 1. Е^-1=Е;

2. (А^-1)^-1=А;

3. Лише квадратна матриця має обернену, причому її порядок такий же, як і порядок даної матриці.

Означення. Квадратна матриця називається особливою (виродженою), якщо її ранг менший її порядку. Квадратна матриця, яка не є особливою, є неособливою (невиродженою).

Теорема 1. Довільна неособлива матриця елементарними перетвореннями рядків може бути зведена до одиничної матриці.

Теорема 2. Матриця має обернену тоді і тільки тоді, коли вона неособлива.

Алгоритм відшукання оберненої матриці:

1. Переконатися, що матриця невироджена;

2. Записати дану матрицю А і дописати справа від неї одиничну матрицю такої ж розмірності;

3. Застосовуючи елементарні перетворення до ‘подвійної матриці’, зводимо матрицю А до одиничної, тоді та матриця, яка з’являється на місці одиничної і є оберненою до матриці А.

Приклад.

1)Знайти обернену матрицю до матриці А

А =

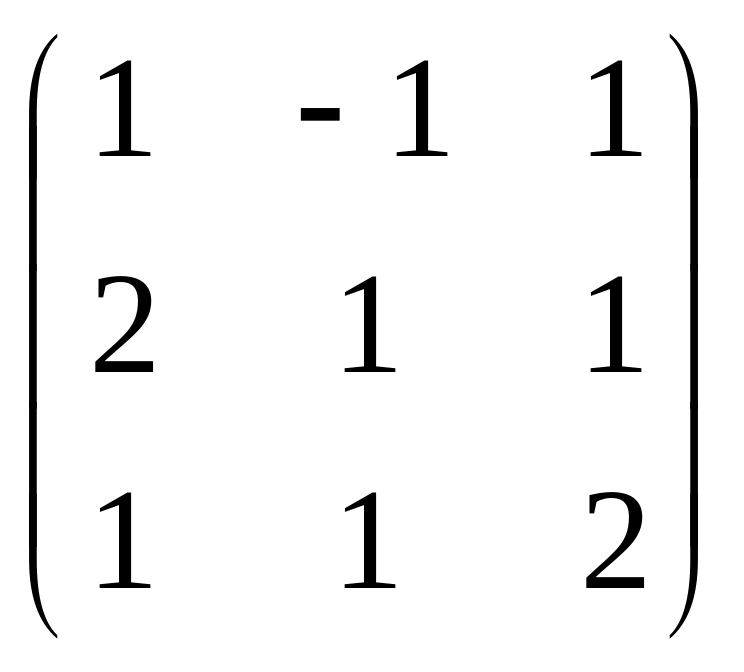
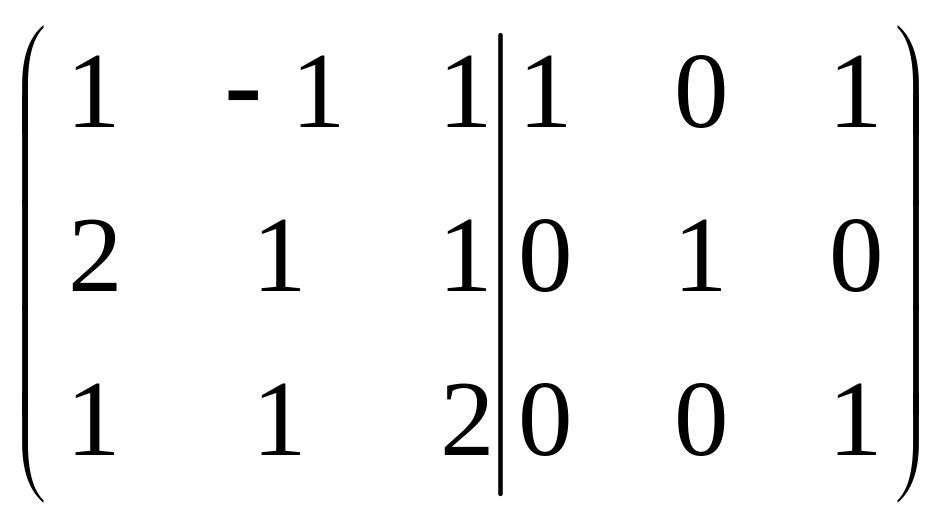
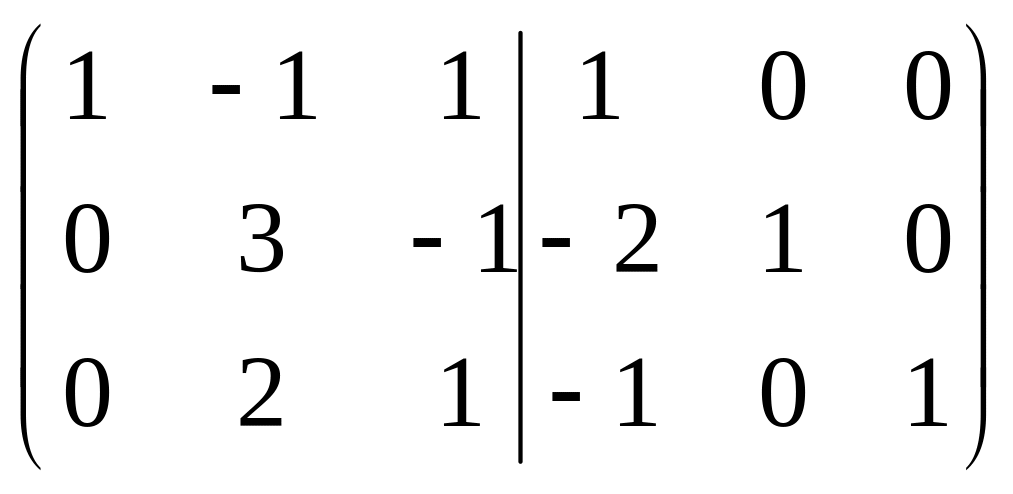
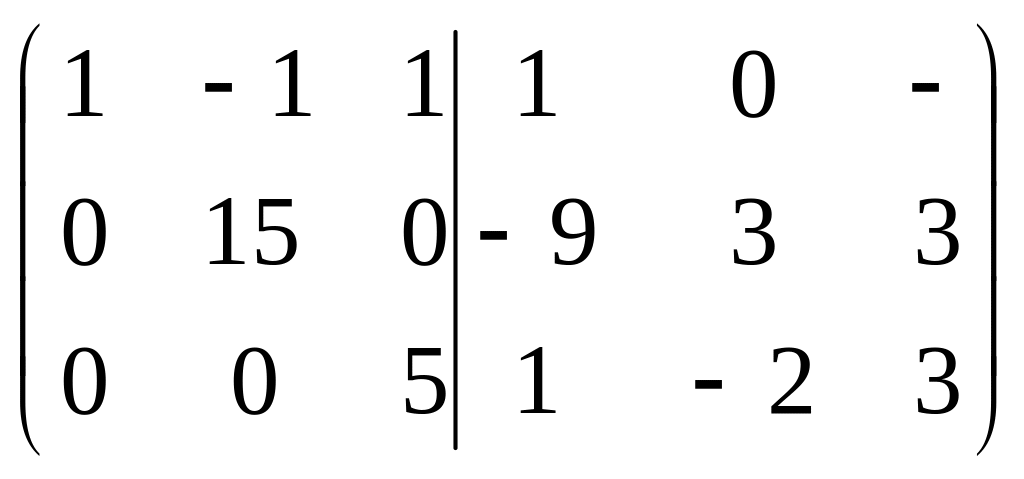
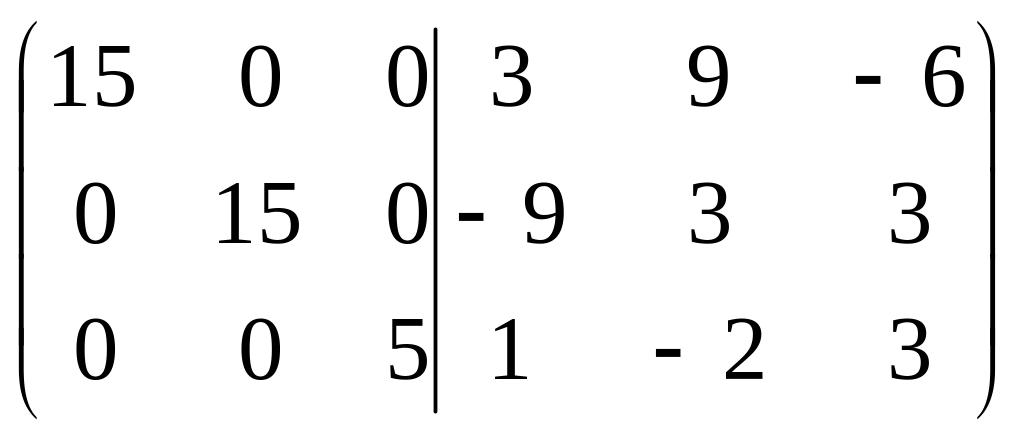
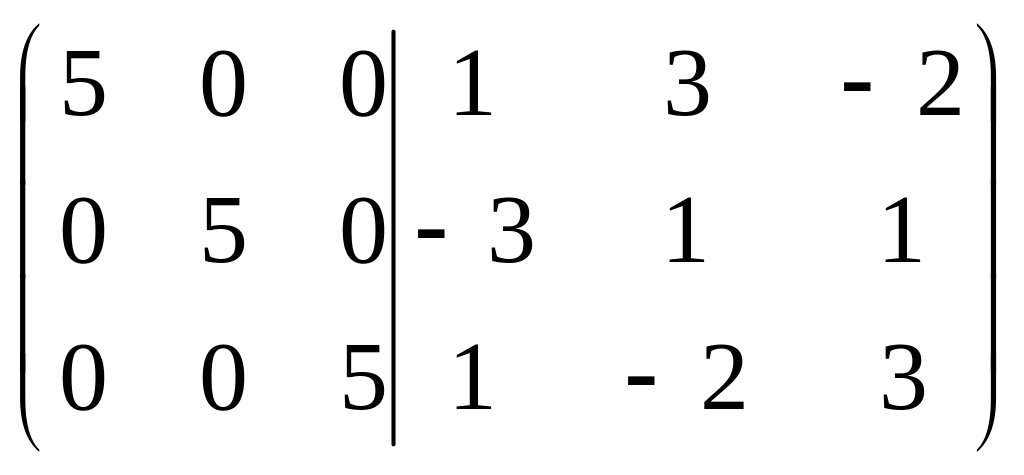
А^-1 =

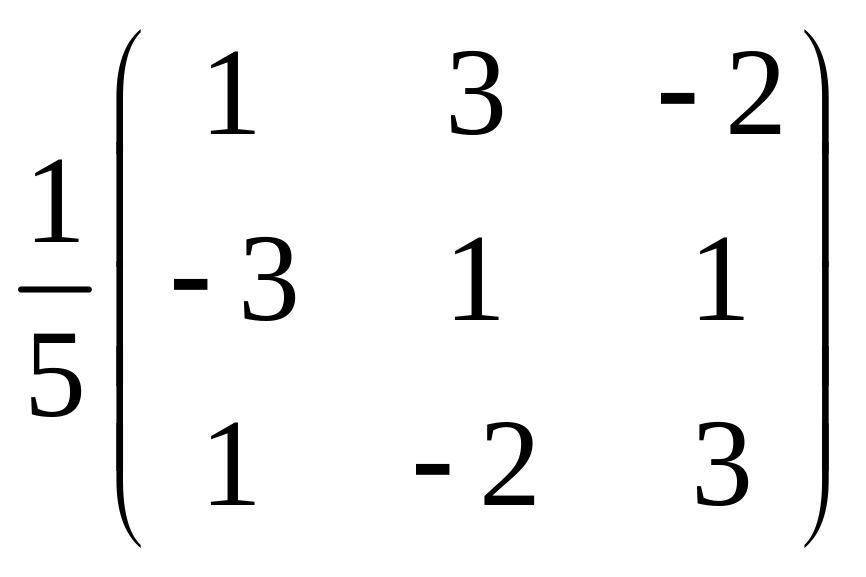
Перевірка: =

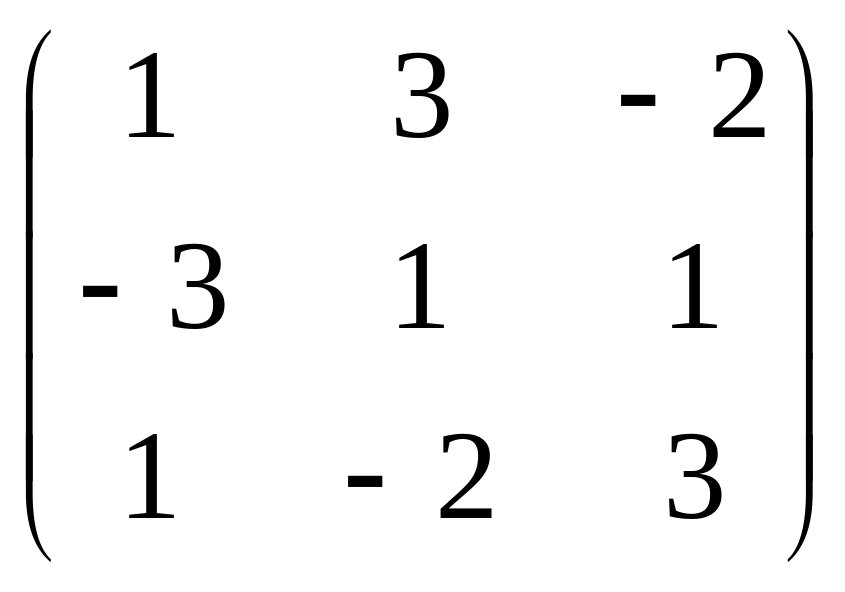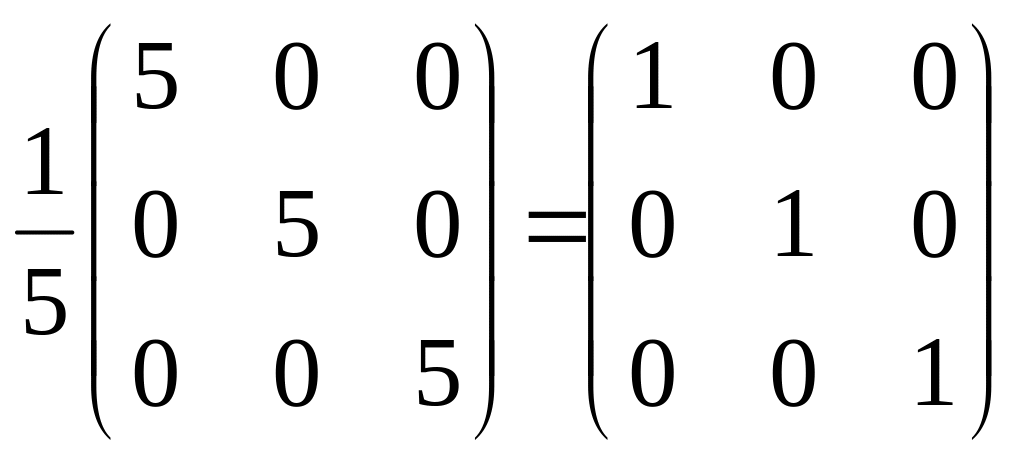
§5. Ранг матриці.

Розглянемо матрицю А =

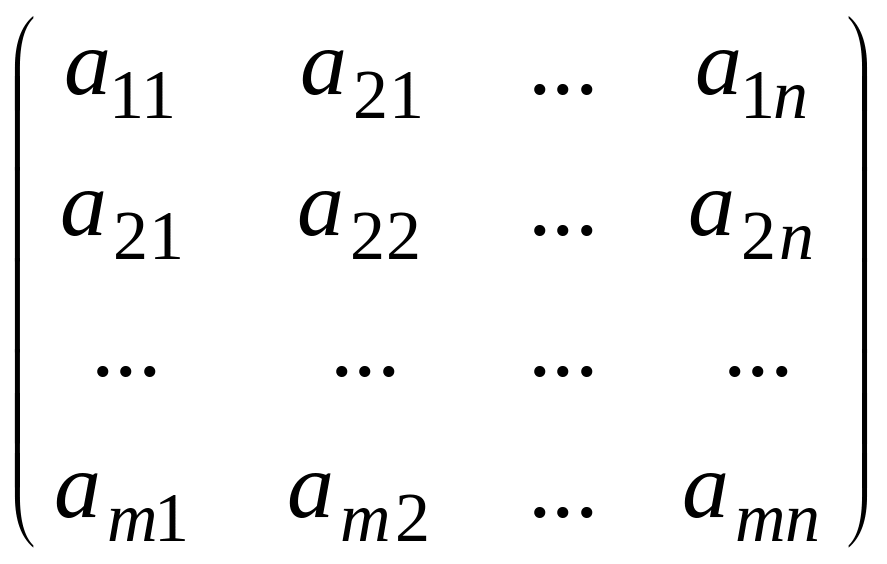
Кожний рядок матриці – це n-мірний числовий вектор, кожний стовпчик - m-мірний числовий вектор.

Означення. Ранг системи векторів-стовпчиків матриці А називається стовпчиковим рангом матриці; ранг системи векторів-рядків матриці А називається рядковим рангом матриці А.

Означення. Елементарними перетвореннями матриці є :

1. перестановка рядків (стовпчиків);

2. множення рядка (стовпчика) на довільне, відмінне від нуля число;

3. додавання рядків (стовпчиків);

4. множення рядка (стовпчика) і додавання його до іншого рядка (стовпчика).

Рангом матриці називається кількість лінійно незалежних векторів-рядків цієї матриці.

Обчислюють ранг матриці за допомогою елементарних перетворень, зводячи матрицю до виду трикутника або трапеції. Ранг матриці дорівнює кількості ненульових рядків в остаточній матриці. Якщо методом елементарних перетворень матриця звелася до виду трикутника, то її ранг дорівнює кількості векторів-рядків в даній матриці, а сама система векторів-рядків є лінійно незалежною. Якщо остання матриця набуває виду трапеції (тобто з’являються нульові рядки в ході елементарних перетворень), то ранг матриці менший, ніж кількість рядків в ній і дорівнює кількості ненульових рядків, а сама система векторів є лінійно залежною.

Розвязуючи задачу про знаходження рангу матриці, ми одержуємо не лише ранг матриці,а й ранг системи векторів-рядків,а також базис цієї системи векторів-рядків. Базис системи векторів-рядків утворюють лінійно незалежні вектори-рядки, які при елементарних перетвореннях не обнулилися.

Приклад.

1) Обчислити ранг матриці в залежності від параметра k:

1. Якщо k-12=12 => k=0, то r=2;

2. Якщо k0, то r=3.