§3. Зв’язок між матрицями лінійного оператора в різних базисах.

Лема. Нехай

A = B =

матриці над полем Р. Якщо для довільного рядка (х₁,х₂,…,х_n) з елементами з поля Р

(x₁,x₂,…,x_n)A=(x₁,x₂,…,x_n)B, то А=В.

Теорема 4.Якщо лінійний оператор А простору V_n задається в базисі {e₁,e₂,…,e_n}матрицею А, то в базисі {e₁,e₂,…,e_n} він задається матрицею А=ТАТ^-1, де Т – матриця переходу від базису {e_i} до базису {e_i}. Нехай {e₁,e₂,…,e_n} – старий базис, {e₁,e₂,…,e_n} – новий базис, тоді кожний з {е_i} можна розкласти по векторам базису {e_і}, тобто

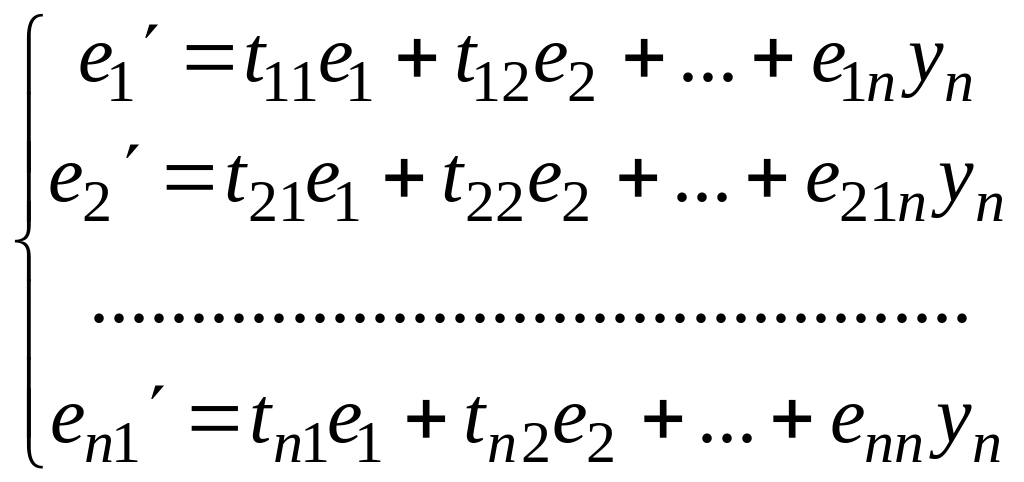
T =

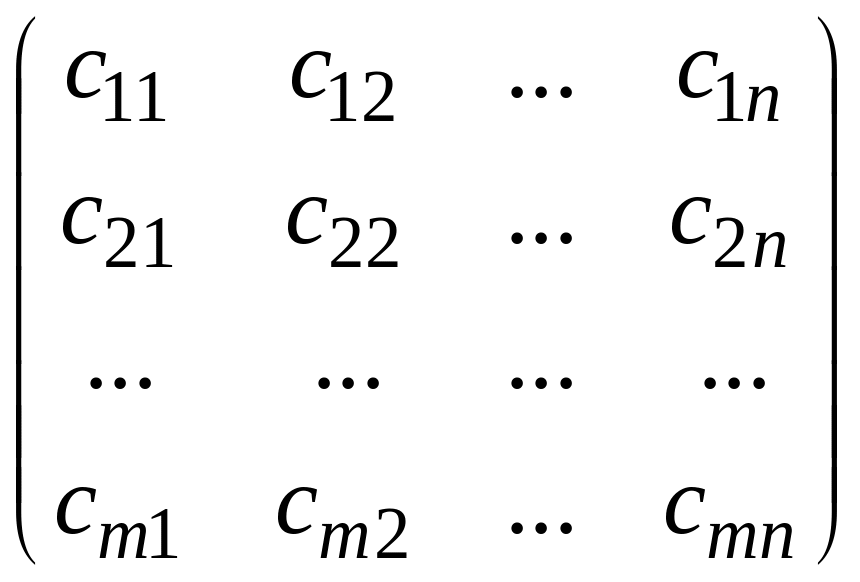
матриця переходу від базиса {e_i} до базису {e_i}.

[x] _e = [x]_eTee^ – зв’язoк між координатами вектора в різних базисах.

§4. Операції над лінійними операторами.

Означення. Оператор S, який кожному вектору х є Vn ставить у відповідність вектор хА+хВ, називається сумою операторів А і В і позначається S=A+B. Це означає, що

x є Vn (хS=хА+хВ ) .

Сума лінійних операторів є лінійним оператором.

Властивості додавання лінійних операторів:

1) Асоціативність  А,В,С ((А+В)+С=А+(В+С));

2) Комутативність  А,В (А+В=В+А);

3) Нульовий оператор О відіграє роль нуля, тобто  А (А+О=О+А=А);

4) Протилежний оператор –А:  А (А+(-А)=(-А)+А=О).

Отже, множина Vn^ всіх лінійних операторів простору Vn з введеною на ній операцією додавання є адитивною абелевою групою.

Означення. Добутком лінійних операторів А і В називається оператор D, який визначається формулою

 х є Vn (xD=(xA)B) і позначається D=AB.

Ця операція складається з послідовної дії операторів А і В. Операція множення лінійних операторів асоціативна

 А,В,С ((АВ)С=А(ВС)) .

В множині операторів виконуються дистрибутивні закони:

 А,В,С ((А+В)С=АС+ВС)

 А,В,С (С(А+В)=СА+СВ).

Отже, множина Vn^ є кільцем.

Означення. Добутком лінійного оператора А на число k називається оператор В, який визначається формулою

 х є Vn k є Р (хВ=kxA)

і позначається В=kA.

Добуток лінійного оператора А на число k є лінійним оператором.

Властивості :

1. А (1А=А);

2. k,m є Р A (k(mA)=(km)A);

3. k,m є P A ((k+m)A=kA+mA);

4. k є P A,B (k(A+B)=kA+kB).

Отже, множина Vn^ всіх лінійних операторів є лінійним простором V_n над полем Р, утворює лінійну алгебру і векторний простір.

Теорема 5. Алгебра V_n^ лінійних операторів n-мірного векторного простору V_n над полем Р ізоморфна алгебрі М_n матриць n-го порядку над полем Р :

1. матриця суми лінійних операторів в довільно вибраному базисі дорівнює сумі матриць доданків в тому ж базисі;

2. матрця добутку лінійних операторів в довільно вибраному базисі дорівнює добутку матриць-співмножників в тому ж базисі;

3. матриця добутку kA лінійного оператора А на деяке число k в довільно вибраному базисі дорівнює добутку матриці оператора А в тому ж базисі на число k.

§5. Область значень і ядро лінійного оператора. Ранг і дефект лінійного оператора.

Теорема 6. Образ будь-якого лінійного підпростору U простору V_n відносно довільного лінійного оператора А також є лінійним підпростором простору Vn.

Означення. Сукупність образів всіх векторів простору V_n називається областю значень лінійного оператора А і позначається ІmA.

Область значень ImA є лінійним підпростором простору V_n.

Означення. Розмірність області значень ImА називають рангом лінійного оператора А і позначають RangA.

Теорема 7. Ранг будь-якого лінійного оператора простору V_n дорівнює рангу матриці цього оператора в довільно вибраному базисі

dim(ImA)=r(A).

Означення. Ядром лінійного оператора А простору V називається сукупність всіх векторів цьoго простору, які відображаються оператором А в нульовий вектор  і позначається KerA.

KerA={xx є V, xA=}V

KerA є лінійним підпростором простору V.

Означення. Розмірність ядра оператора називається дефектом цього оператора і позначається dim(KerA).

Теорема 3. Сума рангу і дефекта будь-якого лінійного оператора А простору V дорівнює розмірності n цього простору.

dim(ImA)+dim(KerA)=dimV