§3. Ортогональний базис.

Теорема 5. Якщо вектор а ортогональний кожному з векторів b₁,b₂,…,b_k, то він ортогональний і будь-якій лінійній комбінації цих векторів k_ib_i,I=1,…,k.

Означення. Система векторів а₁,а₂,…,а_n називається ортогональною, якщо будь-які її два вектори ортогональні,тобто (а_i,а_j)=0 для ij.

Теорема 6. Будь-яка ортогональна система ненульових векторів лінійно незалежна.

Наслідок. Будь-яка ортогональна система n ненульових векторів n-мірного евклідового простору Е_n є ортогональним базисом цього простору.

§4. Ортонормований базис.

Означення. Вектор а, довжина (норма) якого дорівнює 1, називається нормованим.

Означення. Базис е₁,е₂,…,е_n евклідового простору Еn називається ортонормованим, якщо він ортогональний і всі його вектори нормовані, тобто

(е_i,е_j)=

Наслідок. В кожному евклідовому просторі Е_n існують ортонормовані базиси.

§5. Ортогональне доповнення підпростору.

Нехай U – деякий підпростір евклідового простору Еn.

Означення. Вектор а простору Еn називається ортогональним підпростору U (записують а U), якщо він ортогональний довільному вектору цього підпростору.

Теорема 10. Для того, щоб вектор а був ортогональний підпростору U достатньо, щоб він був ортогональний кожному вектору деякого базиса цього підпростору.

Означення. Підпростори U i V простору Е називаються ортогональними і позначають UV, якщо кожний вектор u є U ортогональний кожному вектору v є V.

Теорема 11. Для того, щоб підпростори U i V простору Е були ортогональними достатньо, щоб кожний вектор деякого базиса підпростору U був ортогональний кожному вектору деякого базиса підпростору V.

Означення. Підпростір U^ всіх векторів простору Е, ортогональних підпростору U, називається ортогональним доповненням підпростору U.

Теорема 12. Евклідів простір Еn є прямою сумою кожного свого підпростору U і його ортогонального доповнення U^:

Еn=U U^.

Наслідок. DimEn=dimU+dim U^.

Приклад.

1. Ортогоналізувати систему векторів:

b₁=(1,2,3,4), b₂=(0,5,0,5), b₃=(8,10,-8,14)

Процес ортогоналізації застосовується лише до лінійно незалежної системи векторів, тому перевіримо дану систему на лінійну залежність склавши матрицю з координат даних векторів і знайдемо її ранг.

A = r(A)=3

Отже, вектори b₁,b₂,b₃ утворюють лінійно незалежну систему векторів. За перший вектор с₁ ортогональної системи візьмемо вектор b₁:

с₁=b₁=(1,2,3,4).

Далі шукатимемо вектор с₂ у формі лінійної комбінації векторів с₁ і b₂:

с₂=c₁+b₂.

Оскільки вектор c₂ повинен бути ортогональним до с₁, то

(с₁,с₂)=(с₁,с₁+b₂)=(c₁,c₁)+(c₁,b₂)=0 =>

=> =-(c₁,b₂)/(c₁,c₁)=-(1*0+2*5+3*0+4*5)/(1+4+9+16)=-1

Отже, с₂=-с₁+b₁=(-1,3,-3,1).

Вектор с₃ шукатимемо у формі лінійної комбінації векторів с₁,с₂ і b₃:

с₃=₁c₁+₂с₂+b₃.

Оскільки вектор с₃ повинен бути ортогональним до с₁,с₂, то

(с₁,с₃)=(c₁,₁c₁+₂с₂+b₃)=₁(c₁,c₁)+₂(c₁,c₂)+(c₁,b₃)=

=₁(c₁,c₁)+(c₁,b₃)=0

(с₂,с₃)=(c₂,₁c₁+₂с₂+b₃)=₁(c₂,c₁)+₂(c₂,c₂)+(c₂,b3)=

=₂(c₂,c₂)+(c₂,b₃)=0.

Звідки ₁=-(с₁,b₃)/(c₁,c₁) i ₂=-(с₂,b₃)/(c₂,c₂)

₁=-(1*8+2*10-3*8+4*14)/(1+4+9+16)=-2

₂=-(-1*8+3*10+3*8+1*14)/(1+9+9+1)=-3

Отже, с₃=-2с₁-3с₂+b₃=-2(1,2,3,4)-3(-1,3,-3,1)+(8,10,-8,14)= (9,-3,-5,3)

Одержали ортогональну систему:

с₁=(1,2,3,4), c₂=(-1,3,-3,1), c₃=(9,-3,-5,3).

2)Перевірити чи будуть вектори а₁=(1,-2.2,-3) і а₂=(2,-3,2,4) ортогональні, і якщо так, то доповнити систему цих векторів до ортогонального базису простору, в якому вони розглядаються. Перейти від знайденого базису до ортонормованого.

Оскільки (а₁,а₂)=1*2+(-2)*(-3)+2*2-3*4=0, то вектори а₁,а₂ ортогональні. Знайдемо тепер такий вектор

х=(х₁,х₂,х₃,х₄) є Е, що (а₁,х)=(а₂,х)=0.

Звідси одержимо СЛОР:

Загальний розв’язок системи (2х₃-14х₄,2х₃-10х₄,х₃,х₄),x₃,x₄єR

Фундаментальна система розв’язків

{(2,2,1,0),(-17,-10,0,1)}={x,x}.

Вектори x,x фундаментальної системи розв’язків ортогональні до векторів а₁,а₂ (їх знайдено з цієї умови). Якби ще вектори фундаментальної системи були ортогональними, то система векторів а₁,а₂, x,x була б ортогональним базисом простору Е₄ і залишилося б тільки пронормувати його. Але (x,x)0 і тому ортогоналізуємо спочатку систему векторів x,x.

Згідно процесу ортогоналізації маємо

с₁=х₁, с₂=с₁+b₂,

де =-(с₁, x)/(c₁,c₁)=-(34-20)/9=6.

Тоді с₂=6с₁+x=(-5,2,6,1).

Отже, система векторів є ортогональною системою ненульових векторів. Оскільки кількість елементів цієї системи дорівнює розмірності всього простору Е₄,

то а₁,а₂,с₁,с₂ – ортогональний базис простору Е₄. Для перетворення його в ортонормований треба кожен з векторів, що входить до базису, розділити на його норму. Знайдемо

а₂ = = , а₂= , с₁=3, с₂= .

Тоді = =

- ортонормований базис.

3)Знайти ортонормовану фундаментальну систему розв’язків для системи рівнянь :

Загальний розв’язок х=(2х₂+2/7х₄,х₂,-5/7х₄,х₄),x₄ є R.

X1	X2	X3	X4
2	2	0	0
2	-4	-25	-35

ФСР : (2,1,0,0), (2,-4,-25,-35)

Ортогоналізуємо систему:

b₁=a₁=(2,1,0,0)

b₂=b₂+a₂ => (b₁,b₂)=(b₁,b₁)+(b₁,a₂) =>

=-(b₁,a₂)/(b₁,b₁)=-(2*2-1*4+0*0)/(4+1+0+0)=0

b₂=a₂=(2,-4,-25,-35)

b₁= b₂=

Отже, ортонормована фундаментальна система розв’язків : 1/ (2,1,0,0), 1/ (2,-4,-25,-35).

4)При яких значеннях параметра  вектори а₁=(0,1,), а₂=(1,-1,1), а₃=(-2,-1,) утворюють ортогональний базис простору R.

Для того, щоб вектори утворювали ортогональний базис потрібно, щоб (а_i,а_j) = 0.

(а₁,а₂) = 0-1+ = 0

(а₁,а₃) = 0-1+² = 0

(а₂,а₃) = -2+1+ = 0

Отже,  = 1

5)В евклідовому просторі F₃ многочленів степеня не більше 2 над полем R зі скалярним добутком, заданим рівністю (f,g) = ,задані вектори f₁,f₂,f₃. Ортогоналізувати базис f₁ = 1, f₂ = (2х-1),

f₃ = (6х²-6x+1). Знайти координати ₁,₁,₃,₁,₂,₃ многочленів

₁(х) = 1+2х, ₂(х) = 1-5х+6х² в цьому базисі і обчислити їх скалярний добуток двома способами:

(₁,₂) = , (₁,₂) = ₁₁+₂₂+₃₃

1. g₁(x) = f₁ = 1

g₂(x) = f₁+f₂ =+ (2x-1)

(g₁,g ₂) = 0

 = -(g₁,f₂)/(f₂,f₂)= - 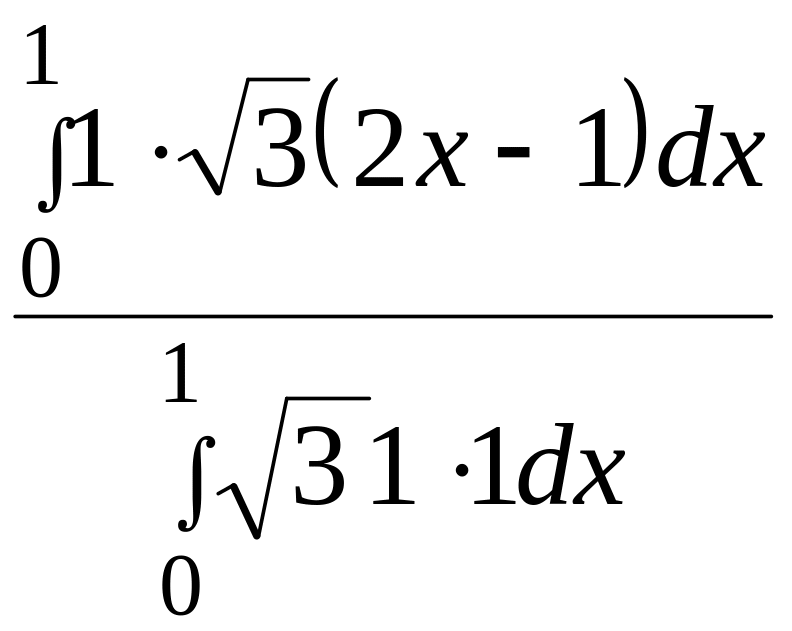=- = 0

g₂(x) = (2x-1)

2. a) ₁ = af₁+bf₂+cf₃

1+2x = a+b (2x-1)+c (6x²-6x+1)

 ₁= 2f₁+ f₂+0*f₃

b) ₂ ==af₁+bf₂+cf₂

1-5x+6x² = a+ (2x-1)+ c(6x²-6x+1)

₂ = 1/2f₁+ /6f₂+ /5f₃

3. (₁,₂) = (1+2x)(1-5x+6x²)dx =

= =

= =

= = 1-3/2-4/3+3 = 7/6

(₁,₂) = 2*1/2+ /3* /6+0* /5 = 1+1/6 = 7/6 6)Знайти ортогональну проекцію а і ортогональну складову b вектора v відносно підпростору L, породженого векторами а₁,а₂,а₃, якщо

а₁ = (2,1,-4), a₂ = (3,5,-7), a₃ = (4,-5,-6), v = (-12,9,-12).

Знайдемо базис L:

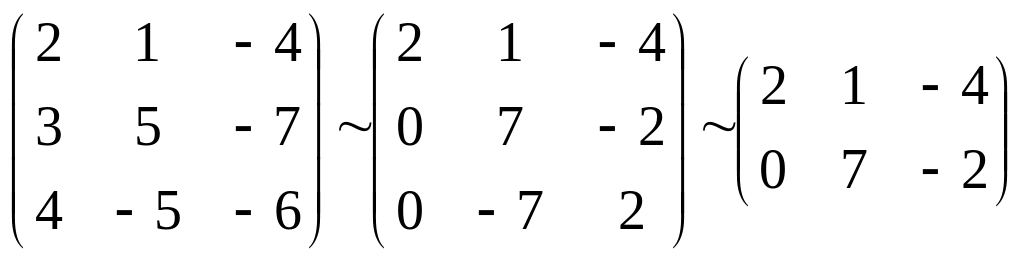
Базис складається з векторів а₁,а₂. Ортогоналізуємо цей базис :

b₁ = a₁ = (2,1,-4)

b₂ = a₂-b₁(a₂,b₁)/(b₁,b₁) = a₂-b₁(6+5+28)/(4+1+16) =a₂-13/7b₁ =

= (3,5,-7)-13/7(2,1,-4) = 1/7(-5,22,3)

Знайдемо ортогональну проекцію а даного вектора v на L :

а = (v,b₁)/(b₁,b₁)b₁+(v,b₂)/(b₂,b₂)b₂ =

= (-24+9+48)/(4+1+16)b₁+(12*5/7+9*22/7-2*3/7):(25/49+484/49+9/7)b₂ = =11/7(2,1,-4)+3/7(-5,22,3) = (1,11,-5).

Знайдемо ортогональну складову b вектора v відносно L :

b = v-a = (-12,9,-12)-(1,11,-5) = (-13,-2,-7).