Лекция 12. Численное решение систем дифференциальных уравнений в частных производных.

Уравнение с частными производными описывают многие физических процессов в таких областях, как механика сплошных сред, термодинамика, квантовая механика, электродинамика, теория упругости и многие другие. Поэтому раздел математики, изучающий свойства возможных решений уравнений с частными производными, называется математической физикой, а сами уравнения часто называют уравнениями математической физики.

Аналитическое решение уравнений с частными производными удается получить лишь в отдельных практически важных случаях, и поэтому значение численных методов для решения задач, которые описываются с помощью этих уравнений, очень важно. Математическими моделями многих физических процессов являются линейные дифференциальные уравнения второго порядка. Поэтому основное внимание в этом разделе уделяется именно этим уравнениям.

12.1. Уравнения математической физики.

Постановку задач для уравнений математической физики приведем для классических уравнений параболического, гиперболического и эллиптического типов. В этих уравнениях чаще всего независимыми переменными являются время и пространственные координаты, от которых зависит функция решения. Такие уравнения описывают множество реальных физических процессов, свойства которых изменяются не только во времени, но и в пространстве.

Задача называется стационарной, если ее решение не зависит от времени, и нестационарной - если такая зависимость существует. Задачи с одной пространственной переменной называются одномерными, с двумя переменными - двумерными, с тремя - трехмерными.

Приведем уравнения канонической форме, которая имеет две пространственные переменные и является линейным относительно вторых производных:

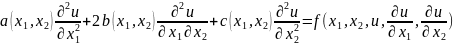
Коэффициенты a, b, с - это функции, которые дважды непрерывно-дифференцированы и не равны нулю одновременно. В зависимости от значений этих функций различают несколько типов квазилинейных дифференциальных уравнений с частными производными второго порядка. Чтобы определить тип уравнения в заданной точке (х₁, х₂) области пространства, вычислим значения D = b²-ас. Дифференциальное уравнение является параболическим, если D = 0, гиперболическим - когда D> 0 и эллиптическим - когда D <0. Следует отметить, что тип определенного уравнения может меняться в зависимости от значений (х₁, х₂) координат точки.

12.1.1. Уравнения параболического типа.

К уравнениям параболического типа относятся уравнения теплопроводности или диффузии вида

где а - коэффициент теплопроводности (если u - температура) и массопереноса (если u - концентрация, давление в задачах фильтрации). Поскольку уравнение содержит производную по времени, для его решения необходимо дополнительно задавать только начальные (для t = 0), так и граничные условия (для х = 0, х = l, t> 0) (рис. 12.1).

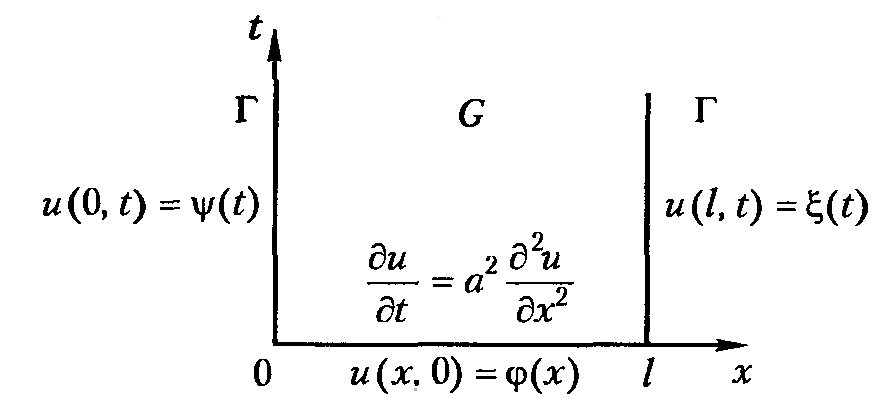
Рисунок 12.1 – Область определения решения одномерного уравнения теплопроводности.

12.1.2. Уравнения гиперболического типа.

Примером уравнений гиперболического типа является волновое уравнение

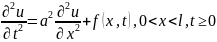
описывающее малые продольные колебания стержня и поперечные колебания струны, где u - отклонение от положения равновесия и а - скорость распространения возмущения. Волновое уравнение описывает процесс распространения малых акустических колебаний.