Лекция 7. Решение систем линейных алгебраических уравнений.

7.1. Область применения слау в задачах математического моделирования эмс.

В линейной алгебре рассматриваются четыре класса основных задач: решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителей, нахождение обратных матриц, определение собственных значений и собственных векторов матриц. Все эти задачи имеют важное прикладное значение при решении различных проблем науки и техники.

Такого рода задачи появляются при решении большого числа технических задач. Расчеты установившихся режимов в электрических схемах в конечном итоге сводятся к составлению и решению СЛАУ. Необходимость решения СЛАУ высоких порядков возникает в процессе реализации алгоритмов решения уравнений в частных производных методами конечных элементов.

Кроме того, задачи линейной алгебры являются вспомогательными при реализации многих алгоритмов вычислительной математики, обработки результатов экспериментальных исследований. Мы уже сталкивались с необходимостью решать СЛАУ при отыскании канонических интерполяционных полиномов, при решении задач аппроксимации функций с помощью МНК.

Постановка задачи. Необходимо решить СЛАУ вида

(7.1)

где x_k – неизвестные величины; a_ij – заданные элементы расширенной матрицы системы уравнений, известные числовые коэффициенты.

СЛАУ может быть представлена в виде

СЛАУ часто записывают в матричной форме:

где А - матрица коэффициентов системы размерности n x n; b – вектор-столбец свободных членов длиной n; x – вектор-столбец неизвестных длиной n;

При формальном подходе решение этих задач не встречает затруднений: решение системы можно найти, раскрыв определители в формуле Крамера; для нахождения собственных значений матрицы достаточно выписать характеристическое уравнение и найти его корни. Однако эти рекомендации встречают возражения со многих сторон.

Так, при непосредственном раскрытии определителей решение системы с n неизвестными требует порядка n(n+1)n! арифметических операций. Так, например, для вычисления одного определителя при n=100 нужно выполнить 10¹⁵⁷ операций с действительными числами. Такое число операций за приемлемое время не в состоянии выполнить самые могущественные современные суперкомпьютеры, и даже в далекой перспективе это будет невозможно.

Другой причиной, по которой эти классические способы неприменимы даже при малых n, является сильное влияние на окончательный результат округлений при вычислениях. Результат вычислений часто далек от истинного значения из-за влияния вычислительной погрешности. Точно так же обстоит дело при нахождении собственных значений матриц с использованием явного выражения характеристического многочлена.

Для решения СЛАУ применяют в основном два класса методов: прямые и итерационные. Прямые методы являются универсальными и применяются для решения систем сравнительно невысокого порядка (n ~ 200). Итерационные методы выгодно использовать для СЛАУ высокого порядка со слабо заполненными матрицами.

7.2. Прямые методы решения слау.

Прямые методы являются аналитическими, а потому обеспечивают точное решение СЛАУ. К прямым методам относятся упоминавшийся выше метод Крамера и метод обратной матрицы.

Если СЛАУ записать в матричной форме:

то, умножая обе части этого равенства на обратную матрицу A^-1, получим решение в виде:

Вычисление элементов обратной матрицы аналитическим образом приводит к необходимости вычисления n² определителей порядка n. Это чрезвычайно трудоемкая задача, способная при относительно небольших порядках СЛАУ (n =50) перегрузить любой компьютер.

Менее трудоемким является метод Крамера. Значения неизвестных определяются по формуле:

Этот метод требует вычисления n+1 определителей порядка n.

Еще одним примером прямых методов является метод последовательного исключения, или метод Гаусса.

Применение метода Гаусса состоит в следующем.

Первое уравнение системы (7.1) делим на коэффициент а₁₁. Получим следующее уравнение:

где c_1j = a_1j/a₁₁; y₁ = b₁/a₁₁.

Из этого уравнения несложно выделить переменную x₁ и подставить полученное выражение в остальные уравнения системы.

Этот процесс можно последовательно применять к оставшимся (n-1) уравнениям исходной системы уравнений.

В итоге такого процесса система уравнений преобразуется к следующему виду:

Последнее уравнение дает нам решение для переменной x_n.

Выполняя обратный ход по уравнениям системы, мы последовательно можем вычислить все переменные системы уравнений.

Сущность метода Гаусса состоит в преобразовании исходной матрицы коэффициентов СЛАУ в нижнюю треугольную матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю.

Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно 2/3 n³. Контроль полученных решений можно провести путем их подстановки в исходную СЛАУ и вычисления невязок r_к, разностей между правыми и левыми частями уравнений

При малой погрешности решений величины r_к будут близки к нулю.

Пример 7.1. Определение токов в ветвях схемы.

Для заданной схемы определить токи в отдельных ветвях методом контурных токов.

Параметры элементов схемы :

R₁=24 Ом, R₂=70 Ом, R₃=44 Ом, R₄ =12 Ом, R₅=20 Ом,R₆=30 Ом, E₂=40 B,

E₃=19,6 B, J_К3=0,1 A.

1. Попередньо перетворимо схему шляхом заміни джерела струму J_К3 на джерело е.р.с. Е₃' (рис. 2.2), де Е₃'= J_К3∙R₃=0,1∙44=4,4 B - еквівалентне джерело е.р.с.

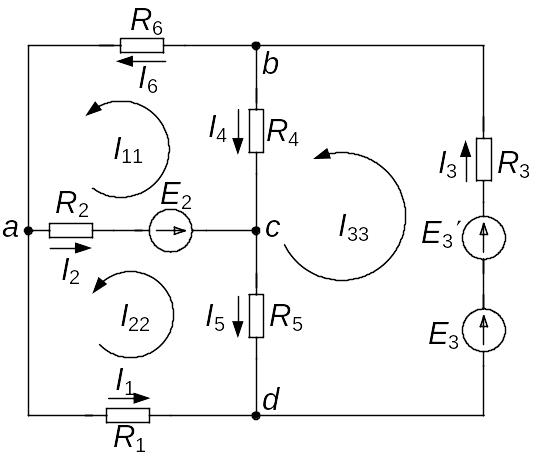
2. Довільно вибираємо позитивні напрямки контурних струмів I₁₁, I_{22 ,}I₃₃.

3. Складаємо систему рівнянь за другим законом Кірхгофа для контурних струмів:

де R₁₁= R₂+R₄+R₆ =112 Ом – власний опір першого контуру;

R₂₂ =R₁+R₂+R₅ =114 Ом – власний опір другого контуру;

R₃₃ =R₄+R₅+R₃ =76 Ом – власний опір третього контуру;

R₁₂= R₂₁= -R₂ = -70 Ом – опір суміжної вітки між 1-м і 2-м контурами, знак “мінус“ відповідає випадку, коли контурні струми вітки мають протилежні напрями;

R₁₃ =R₃₁ = - R₄ = -12 Ом – опір суміжної вітки між 1-м і 3-м контурами;

R₂₃ =R₃₂ = - R₅ = -20 Ом – опір суміжної вітки між 2-м і 3-м контурами;

E₁₁ = E₂ =40 B – контурна е.р.с. 1-го контуру;

E₂₂ = -E₂ = – 40 B – контурна е.р.с. 2-го контуру, має знак “мінус”, оскільки напрям дії е.р.с. протилежний напряму контурного струму I₂₂;

E₃₃ = E₃+E₃' = 24 B – контурна е.р.с 3-го контуру.

Підставляємо числові значення у систему рівнянь і розв’язуємо ії за формулами Крамера

Знаходимо головний визначник системи:

Допоміжні візначники:

Тоді контурні струми дорівнюють:

Примеры решения СЛАУ.

Пример 7.2. Решение СЛАУ методом обратной матрицы в MS EXCEL

Найдем матрицу, обратную матрице А. Для этого в ячейку А9 введем формулу =МОБР(А2:С4). После этого выделим диапазон А9:С11, начиная с ячейки, содержащей формулу. Нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ENTER. Формулавставится как формула массива. =МОБР(А2:С4).

Найдем произведение матриц А^-1·b. В ячейки F9:F11 введем формулу: =MУMHOЖ(A9:C11;D2:D4) как формулу массива. Получим в ячейках F9:F11 корни уравнения:

Пример 7.3. Решение СЛАУ методом Крамера в MS EXCEL.

Исходные данные и необходимые формулы

Полученные решения

Другие прямые методы решения СЛАУ: метод LU-разложения, метод Холесского, метод вращений и много-много других …

Основным недостатком прямых методов решения СЛАУ является очень большой объем арифметических операций, выполняемых над действительными числами. Так как объем вычислений практически экспоненциально нарастает с ростом порядка СЛАУ, то ошибки округления могут приводить к существенной неточности получаемых результатов. Для получения удовлетворительной точности рекомендуется избегать ситуаций, когда отдельные коэффициенты СЛАУ значительно (3-4 порядка) отличаются друг от друга.

Также обязательной процедурой является численная проверка полученного решения.