5.3. Малая помехоустойчивость метода наименьших квадратов при решении задач идентификации

Метод наименьших квадратов, основанный на «внутреннем» критерии (среднеквадратичная ошибка на всех точках), не пригоден для нахождения модели оптимальной сложности из-за слабой помехоустойчивости внутренних критериев, к которым он относится. Чтобы показать это, проделаем следующий опыт: пользуясь уравнением третьей степени заполним таблицу исходных данных у = f (х). Теперь «забудем» исходный полином и попробуем найти его при помощи метода наименьших квадратов. Для этого последовательно опробуем полиномы при нарастающей сложности:

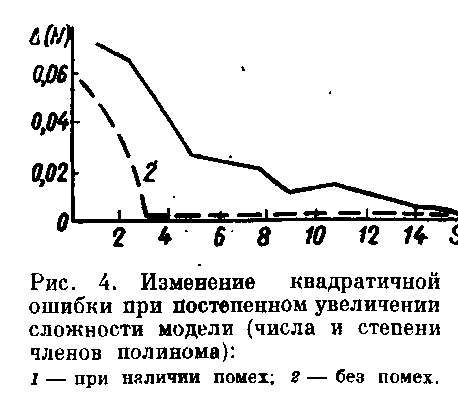Изменение среднеквадратичной ошибки будет следующим: для уравнения первой степени δ² = = 25%, второй— δ² = 15%, третьей — δ² = 0%, четвертой δ² = 0% и т. д. (показано на рис. 5.1 пунктиром). Таким образом, при полном отсутствии помех метод позволяет «открыть» истинное уравнение. Легко убедиться, что при наложении на исходные данные очень небольшого шума (Δy = ±0,01) получается кривая, показанная сплошной линией (рис. 5.1). Кривая подтверждает правило «чем сложнее модель, тем она точнее».

При наличии даже очень малых неточностей измерений (помех) с помощью критерия Δ²(N) нельзя отличить слишком сложные (переусложненные) модели от модели оптимальной сложности, отвечающей действительному процессу. Задачу открытия единственной модели оптимальной сложности решают методы самоорганизации моделей, основанные на помехоустойчивых, «внешних» критериях. Как увидим ниже, для экстраполяции (прогнозирования) метод наименьших квадратов тоже не пригоден.

Это не исключает эффективности метода наименьших квадратов при решении задачи приближенной аппроксимации функций внутри области интерполяции, где достаточно густо заданы опытные точки. Собственно говоря, метод и был задуман Гауссом для решения задачи интерполяции.

5.3.1. Теория множественности моделей

Теория множественности моделей утверждает, что по экспериментальным данным принципиально нельзя найти единственную модель. Например, в качестве полинома регрессии можно взять полином любого вида и любой степени, и для каждого из них регрессионный анализ укажет значения коэффициентов. В любом достаточно сложном уравнении подбираются оценки коэффициентов так, чтобы ошибка на интервале наблюдения (интерполяции) была мала или даже равна нулю. Например, если задано пять экспериментальных точек, то уравнение, имеющее пять коэффициентов (или параметров), дает кривую, точно проходящую через все заданные точки. В этом и состоит теория множественности моделей. Отсюда следует, что для каждого объекта, рассматриваемого как некоторый «черный ящик», можно составить не одну единственную, а бесконечное множество моделей, имеющих одинаковые или почти одинаковые внешние проявления. Так, ясно, что не раскрыв электрический выключатель, мы никаким способом не можем установить, сколько разрывов электрической цепи он выполняет: один, два или три.

По этому поводу У. Р. Эшби пишет: «Время простых моделей прошло... С тех пор, как было доказано (Шенноном в 1938 г. для релейных сетей и Мак-Каллоком и Питтсом в 1943 г. для сетей из простых нейроноподобных элементов), что любое поведение машины, поддающейся описанию, может быть реализовано не одной машиной, а бесконечным рядом их, разработка новой модели показывает только, что ее автор не усвоил значения работ Шеннона, Мак-Каллойа и Питтса» [89, 90].

Во многих научных работах еще до сих пор авторы указывают, что их теория или формула дала кривую, которая весьма близко прошла через экспериментальные точки. Такого рода «доказательства» правильности теорий нельзя принимать серьезно.

Решение вопроса о выборе единственного уравнения регрессии оптимальной сложности дает принцип внешнего дополнения.

Только внешнее дополнение может служить арбитром при сравнении противоречащих теорий. Ошибка, измеренная на всех экспериментальных точках, не является внешним дополнением.