4. Варіація функції та приріст функціоналу.

Нехай функціонал визначений на класі функцій D, і — довільні функції даного класу D. Функція, яка дорівнює різниці функцій і , називається приростом або варіацією аргументу функціоналу і позначається : .

Тоді .

Різниця називається приростом функціоналу , який відповідає варіації аргументу.

Зазначимо, що похідна варіації функції дорівнює варіації похідної: Дійсно,

Якщо нескінченно малому приросту функції відповідає нескінченно малий приріст функціоналу  , то такий функціонал називається неперервним. Точніше, функціонал називається неперервним на кривій в смислі відстані kтого порядку, якщо за довільно заданому знайдеться таке , що при виконанні умови справджується нерівність

Функціонал називається лінійним, якщо виконуються умови:

1. Функціонал від алгебраїчної суми функцій дорівнює відповідній алгебраїчній сумі функціоналів:

2. Сталий множник можна виносити за знак функціоналу:

5. Перша та друга варіації функціоналу.

Якщо для довільно малої варіації аргументу приріст функціоналу можна подати у вигляді суми головної частини, лінійної відносно , та нескінченно малої вищого порядку порівняно з : де — лінійний відносно функціонал, — нескінченно малий вищого порядку порівняно з функціонал: , тобто, де то сам функціонал називається варійовним, а головна лінійна відносно частина його приросту називається диференціалом або варіацією функціоналу і позначається : де . (Перше означення варіації функціоналу).

При дослідженні функціоналів варіація функціоналу відіграє роль, аналогічну тій, яку виконує при дослідженні функцій диференціал. В таблиці 1 наведено відповідність понять диференціального та варіаційного числень.

Таблиця 1

№ п/п	Диференціальне числення	Варіаційне числення
	Аргумент — числова змінна х	Аргумент — числова функція
	Залежна змінна — числова y	Залежна змінна — числова I
	Приріст аргументу	Варіація аргументу
	Приріст функції	Приріст функціоналу
	Диференціал функції	Варіація функціоналу
	Другий диференціал функції	Друга варіація функціоналу
	Необхідна умова екстремуму	Необхідна умова екстремуму
	Стаціонарна точка функції	Стаціонарна функція (допустима екстремаль) функціоналу
	Достатня умова екстремуму:	Достатня умова екстремуму:

Варіацію називають також варіацією першого порядку або першою варіацією функціоналу . Варіацію другого порядку введемо аналогічно тому, як це робиться для диференціала другого порядку функції.

Візьмемо довільну допустиму функцію і довільну її варіацію таку, що функція є допустимою функцією. Зафіксуємо та і розглянемо однопараметричну сім'ю функцій , де — деяке число. Функціонал на вказаній сім'ї функцій є функцією параметра :

.

Розкладемо цю функцію за формулою Тейлора до квадратичного члена включно в околі точки :

де залишковий член є нескінченно малою вищого порядку порівняно з : .

Тоді варіаціям першого та другого порядку можна дати такі означення.

Варіацією або першою варіацією функціоналу  називається значення першої похідної функції при :

(Друге означення варіації функціоналу).

Можна показати, що це означення першої варіації рівносильне наведеному раніше. На практиці зручніше користуватись останнім означенням.

Другою варіацією функціоналу або варіацією другого порядку називається значення другої похідної функції при :

Приклад 3. Знайти варіацію функціоналу а)  б)  в)  користуючись першим означенням як головної лінійної відносно частини приросту  .

Розв'язання. а) Знайдемо приріст функціоналу  :

За першим означенням

б) Знайдемо приріст функціоналу :

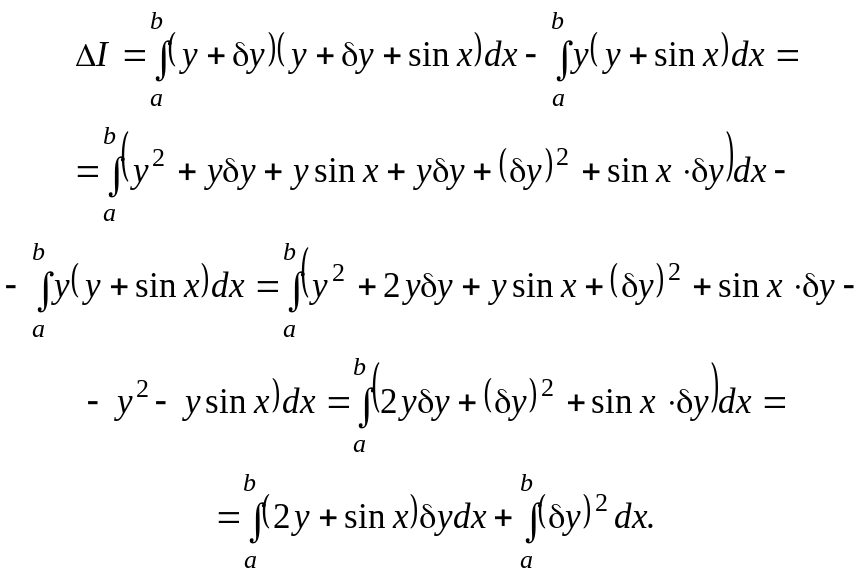
За першим означенням .

в) Знайдемо приріст функціоналу :

За першим означенням .

Приклад 4.Знайти варіацію функціоналу а)  б)  в)  користуючись другим означенням варіації функціоналу як похідної по параметру.

Розв'язання. У відповідності з другим означенням варіації функціоналу маємо:

а) 

б) 

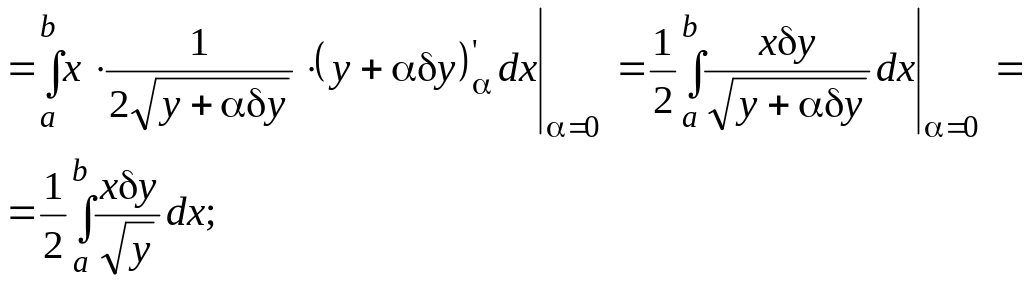
в)