Питання для самоконтролю.

• Сформулюйте задачу дробово-лінійного програмування.

• Дайте економічну інтерпретацію задачі дробово-лінійного програмування.

• Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування.

• У чому принципова відмінність геометричної інтерпретації задачі дробово-лінійного програмування?

• Навколо якої точки здійснюється поворот лінії рівня?

• Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування графічним методом.

Тема 7. Нелінійні оптимізаційні моделі економічних систем.

Лекція 15.

Тема лекції: Задачі нелінійного програмування

Мета: ознайомити студентів з методами розв’язання задач нелінійного програмування.

План лекції

1. Класичні методи розв’язування задач нелінійного програмування.

2. Метод множників Лагранжа.

3. Задачі опуклого прогрмування.

Література:

1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.

2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.

3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.

4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.

1. Класичні методи розв’язання задач нелінійного програмування.

Загальна задача нелінійного програмування полягає у знаходженні максимального(мінімального) значення функції

Z=f(x₁, x₂,….. x_n) →max/ min (1)

за умов

g_i(x₁, x₂,….. x_n) { ≤=≥}b_i, i=1,2…..m (2)

де всі функції (або їх частина) нелінійні.

Функція f з (1) – цільова функція, а умови g_i з (2) - умовами обмеження.

Сукупність змінних, що задовольняють обмеженням (2) задачі називається допустимим розв’язком або планом. Кожному допустимому розв’язку відповідає певне значення цільової функції.

Допустимий розв’язок (план), при якому цільова функція набуває найбільшого (найменшого) значення називається оптимальним планом. Найбільше (найменше) значення функції в допустимій області розв’язків називається глобальним максимумом (мінімумом). Задачі НП розв’язуються значно складніше, ніж задачі ЛП. Для відшукання їх розв’язків немає універсального методу.

Лише для небагатьох типів задач НП розроблені обчислювальні методи їх розв’язання.

Найбільш вивчені задачі з нелінійною цільовою функцією певного виду і лінійними обмеженнями. Для розв’язання таких задач використовується ідея зведення до лінійного вигляду, що допускає застосування симплексного методу. Ще однією особливістю задач НП є наявність точок оптимуму, які можуть бути як граничними, так і внутрішніми точками області допустимих розв’язків.

Як згадувалось вище, найбільш вивченими є задачі з нелінійною цільовою функцією і лінійними обмеженнями, які можна класифікувати таким чином:

• Задачі дробово-лінійного програмування

Z=(∑c_ix_i)/( ∑d_ix_i) →max/ min

за умов

∑a_ijx_j =b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

• Сеперабельна задача НП

f(x₁, x₂,….. x_n) =∑f_i(x_i) →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

• Квадратична задача НП

f(x₁, x₂,….. x_n) =∑c_jx_j +∑∑d_jix_ix_j →max/ min

за умов

∑a_ijx_j{ ≤=≥}b_i, (i=1,2…..m)

x_j ≥0 (j=1,2…..n)

• Задача опуклого програмування

Це задача, в якій цільова функція f і функції обмежень g_i є опуклими (вгнутими) функціями. Суттєвим для цих задач є вимога гладкості, тобто функції f і g_i повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.

Розглянемо задачу (5), якщо на змінні не накладаються умови обмежень.

Така задача вирішується класичними методами дифереціального числення.

Нехай Z=f(x₁, x₂,….. x_n) неприривно – диференційована функція в своїй області визначення. Необхідною умовою екстремуму в точці Х₀ функції Z=f(x₁, x₂,….. x_n) є рівність нулю градієнта функції Z(X₀)=0.Для функції Z=f(x₁, x₂,….. x_n) запишемо матрицю Гессе:

Н=

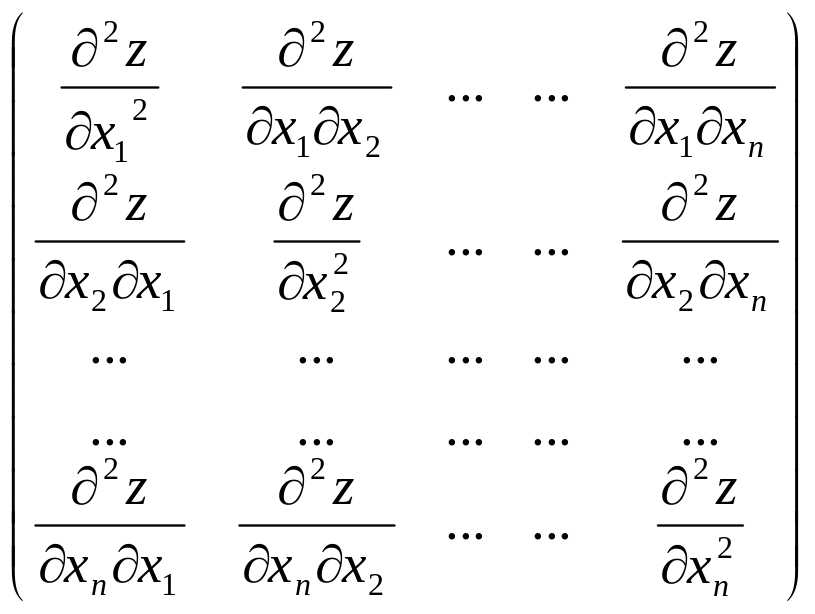
яка складається з частинних похідних другого порядку.

Головні мінори матриці Гессе позначимо:

M₁= , M₂= , ………….,M_n=H,

де f_ij= – значення частинної похідної другого порядку функції Z в точці X₀.

Якщо всі головні мінори M₁, M₂, M₃, …… M_n>0, то Х₀ – точка локального мінімуму. Якщо головні мінори почергово міняють знак, починаючи з мінуса, то точка Х₀ – точка локального максимуму. Проаналізувавши всю область допустимих розв’язків, можна виділити серед локальних екстремумів найбільший і найменший, які і будуть глобальними.