Полупроводники и диэлектрики.

ΔEа –энергия активации проводимости ,т.е. полупроводники и диэлектрик обладают проводимостью в возбужденном состоянии.

Смысл ΔEа – зависит от механизма проводимости и связан с шириной запрещённой зоны или энергией ионизации примеси.

Различия в электропроводности материалов и полупроводников:

Металлы	Полупроводники
σ 102 – 105 1/Ом*см	σ 10-9 – 103 1/Ом*см
σ (t) σ (t) ↓ ρ~ ρ0+αT рост сопротивления, падение σ	σ (t) ~ exp (-ΔEа /KT) сильный з-н роста электропроводности
Не зависит от дефектов и химической чистоты	Зависит от кристаллического совершенства (монокремний ρ~ 0,001-105 Ом*см, поликристаллический ρ>104 Ом*см) и химической чистоты
Не зависит от внешних условий	Зависит он внешних воздействий: - освещение - все виды радиации -давление -магнитные и электрические поля

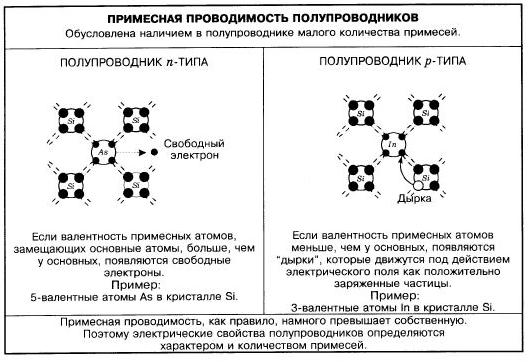
Классификация неметаллических кристаллов по химической связи.

Ионная связь –ионные кристаллы – агрегаты, состоящие из положительных и отрицательных ионов. Являются диэлектриками со слабой ионной проводимостью (электронная отсутствует)

Ковалентная связь –ковалентные кристаллы с решётками алмаза,сфалерита или вюрцита –элементарные полупроводники и полупроводниковые соединения.

Вандервальсова связь –молекулярные кристаллы состоят из слабо связанных между собой молекул (органические кристаллы). Хорошие изоляторы.

Классификация по зонной структуре (энергетическому спектру) и симметрии кристаллических решеток.

Металлы обладают в основном 3-мя типами решёток : ОЦК, ГЦК и гексагональной

Высокопроводящие металлы обладают ГЦК –решёткой.

Полупроводники –алмазные решётки , типа сфалерита или вюрцита.

Диэлектрики – различные типы решёток(ионные кристаллы –ОЦК и ГЦК)

1.2. Электронная теория Друде-Лоренца. Основы классической теории электропроводности. Теория Друде – Лоренца.

Е- напряженность – векторная характеристика, сила действует на положительно заряженный заряд.

F_e=-eE

[Е]=В/м

φ- работа по переносу заряда электрического тока [Дж]

Работа по перенесению единичного заряда Дж/Кл=Вольт

[φ]= Дж/Кл=В

E= -grad φ

φ₁- φ₂=U(B) –напряжение

Характеристика электрического поля.

Когда электрическое поле прикладывают к материалу возникает направленное движение зарядов – электрический ток.

[I]=A – сила тока

j=I/S – плотность тока

Сила тока- количество заряда прошедшее через поперечное сечение проводника.

Закон Ома связывает заряд и электрическое поле.

Плотность тока зависит от характеристик материала.

J=σЕ σ- электропроводность

[σ]=А*м/м²*В=1/Ом*м

ρ^-1=Ом*м – удельное сопротивление

j=Q/t=envt/t=env_др n – концентрация в ед. объема

[n]=1/м³=1/10⁶см³

Vдрейфовая – м/с

Q – количество заряда

V_др=μЕ μ – подвижность свободных носителей заряда

[μ]=м²/с*В

μ – коэффициент пропорциональности между V_др и электропроводностью

j = enμE → σ = enμ

Классическое представление: твердое тело состоит из отдельных атомов, в твердом теле электрон под действием силы движется скачками, между отдельными соударениями электрон движется равноускоренно.

V

V_max

τ- время свободного пробега

F=eE

t

V =V₀+at= (eE/m)/t a=eE/m

V₀=0

V_ср=(V_min+V_max)/2

V_др=(eEτ/2m)= (V_min+V_max)/2

τ

Процесс случайный, но вероятность столкновения в единицу

времени Р=1/τ - величина постоянная. Тогда μ= τе/m μ – подвижность

Подвижность определяется временем свободного пробега

mv_t ²/2 = 3/2 КТ К – константа Больцмана

L_{св.проб.}=(V_t+V_др)* τ V_t>> V_др – условие выполнения закона Ома

L_{св.проб.}= V_t*τ - сотни межатомных расстояний.

Т.о. классическая теория электропроводности за счет введения понятия длины и времени свободного пробега снимала противоречие между двумя экспериментальными законами – вторым законом Ньютона (сила вызывает ускорение) и законом Ома (электрическое поле вызывает движение электронов с постоянной скоростью, а не с ускорением). Однако классическая теория не могла объяснить, почему длина свободного пробега электронов в кристаллах составляет сотни межатомных расстояний. Это удалось объяснить на основе квантовомеханических предствлений о движении электронов в твердых телах.