Глава 2. Элементы высшей алгебры

§ 1. Комплексные числа

Комплексным числом z называют выражение

z = a + ib, (1)

где a и b – действительные числа; i – мнимая единица:

i = или i² = −1; (2)

a – действительная часть числа ( Re z );

b – мнимая часть числа ( Im z ).

(1) – алгебраическая форма записи комплексного числа.

Если а = 0, то 0 + ib = ib – чисто мнимое число;

Если b = 0, то a + i0 = а − действительное число.

Комплексные числа z = a + ib и = a − ib − сопряженные числа.

Два комплексных числа z₁ = a₁ + ib₁ и z₂ = a₂ + ib₂ считаются равными, если a₁ = a₂ и b₁ = b₂.

Комплексное число z = a + ib = 0, когда а = 0, b = 0.

Всякое комплексное число z = a + ib можно изобразить точкой М(а, b) на плоскости OXY:

.

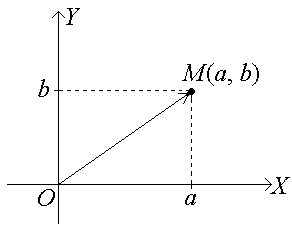Здесь ось ОХ – действительная ось, ось OY – мнимая ось. В этом случае плоскость OXY часто называют комплексной плоскостью. Иногда удобно считать геометрическим изображением комплексного числа

z = a + ib вектор .

Число |z| = − модуль комплексного числа.

Действия над комплексными числами

Пусть даны числа z₁ = a₁ + ib₁ и z₂ = a₂ + ib₂.

1). Сложение и вычитание:

z₁ ± z₂ = (a₁ ± a₂) + i(b₁ ± b₂). (3)

2). Умножение:

z₁∙z₂ = (a₁ + ib₁)∙ (a₂ + ib₂) = (a₁a₂ − b₁b₂) + i(b₁a₂ + a₁b₂). (4)

3). Деление:

= = = =

= + i . (5)

4). Возведение в степень:

Если учесть, что

iⁿ = k N,

то комплексные числа можно возводить в степень.

Пример. Найти z³, если z = a + ib.

□ z³ = (a + ib)³ = a³ + 3a²(ib) + 3a(ib)² + (ib)³ = (a³ − 3ab²) +

+ (3a²b − b³)i. ■

Замечание 1. При п > 3 возведение в степень комплексного числа в алгебраической форме значительно усложняется.

Замечание 2. Умножение, деление и возведение в степень комплексных чисел упрощается, если их представить в тригонометрической или показательной формах.

Тригонометрическая форма записи комплексного числа

Вспомним полярную систему координат:

.

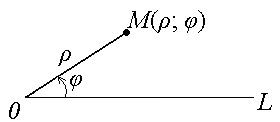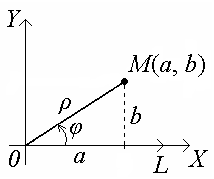
Совместим полюс О с началом координат комплексной плоскости и направим полярную ось по действительной оси ОХ. В результате получим:

.

Из треугольника следует:

а = ρ , b = ρ (ρ ≥ 0).

Тогда

z = a + ib = ρ + i ρ

или

z = ρ( + i ), (6)

(6) – тригонометрическая форма записи комплексного числа.

Здесь

ρ = |z| = − модуль комплексного числа;

φ = arg z = arctg − аргумент комплексного числа.

Отметим следующие соотношения:

φ = arg z = (7)

Аргумент комплексного числа положительный, если он отсчитывается против часовой стрелки; в противном случае – отрицательный. Аргумент комплексного числа определяется неоднозначно, а с точностью до слагаемого 2πk, k Z.

Любое действительное число А можно записать в виде (6):

А = |A|( + i ) при А > 0,

А = |A|( + i ) при А < 0,

0 = 0( + i ).

Действия над комплексными числами в тригонометрической форме

Пусть даны числа

z₁ = ρ₁( + i )

и

z₂ = ρ₂( + i ).

1). Умножение:

z₁∙z₂ = ρ₁ρ₂( + i )( + i ) = ρ₁ρ₂( −

− ) + i( + ) = ρ₁ρ₂( +

+ i ),

т.е.

z₁∙z₂ = ρ₁ρ₂( + i ). (8)

2). Деление:

= = =

= = ( + i ),

т.е.

= ( + i ). (9)

3). Возведение в степень:

Из формулы (8) следует, что при п – целом положительном числе

zⁿ = (ρ( + i ))ⁿ = ρⁿ( + i ), (10)

(10) – формула Муавра.

4). Извлечение корня:

Пусть

= r( + i )

или

ρ( + i ) = r^п( + i ).

Остается определить r и ψ.

У равных комплексных числах модули равны, а аргументы могут отличаться на число, кратное 2π. Значит,

rⁿ = ρ, nψ = φ + 2πk.

Тогда

r = (арифметическое значение), ψ = .

Окончательно,

= = ( + i ), (11)

где k = 0, 1, 2, …, n − 1.

Корень п-ой степени из комплексного числа имеет п различных значений.

Корень п-ой степени из действительного числа А, отличного от нуля, также имеет п значений.

Пример. Пусть z = 1. Найти .

□ Запишем действительное число 1 в тригонометрической форме:

1 = 1∙( + i ).

Тогда

= = = + i , k = 0, 1, 2.

Следовательно,

k = 0: = + i = 1;

k = 1: = + i = − + i ;

k = 2: = + i = − − i . ■

Замечание 3. Из формулы (11) следует, что геометрически точки, соответствующие различным значениям корня п-ой степени из комплексного числа, располагаются в вершинах правильного п-угольника с центром в точке О.

Показательная форма записи комплексного числа

Пусть z = x + iy. Известно, что показательная функция от комплексной переменной z равна

e^z = e^{x + iy} = e^x( + i ). (12)

Свойства показательной функции e^z:

1⁰. = ;

2⁰. = ;

3⁰. = ;

4⁰. = , т.е. показательная функция − периодическая функция с периодом 2πi.

Пусть в (12) х = 0. Тогда

e^iy = + i , (13)

(13) – формула Эйлера.

Заменяя в (13) у на −у, получим

е^−iy = − i . (14)

Складывая (13) и (14), получим

= .

Вычитая из (13) равенство (14), получим

= .

Пусть z = ρ( + i ). По формуле Эйлера (13):

+ i = e^iφ. (15)

Следовательно,

z = ρ e^iφ, (16)

(16) – показательная форма записи комплексного числа.

Действия над комплексными числами в показательной форме

Пусть даны числа

z₁ = ρ₁ и z₂ = ρ₂ .

1). Умножение:

z₁∙z₂ = ρ₁ρ₂ . (17)

2). Деление:

= . (18)

3). Возведение в степень:

zⁿ = ρⁿ . (19)

4). Извлечение корня:

= = , (20)

где k = 0, 1, 2, …, n − 1.

Свойства сопряженных комплексных чисел

1⁰. Сопряженные числа z и имеют:

|z| = | |, arg z = −arg .

2⁰. z∙ = a² + b² или z∙ = |z|² = | |².

3⁰. = ± .

4⁰. = ∙ .

5⁰. =

Пример. 1. Записать комплексное число z в алгебраической, тригонометрической и показательной формах и изобразить его на комплексной плоскости;

2. найти число z¹⁰ и изобразить его на комплексной плоскости;

3. найти все корни уравнения w³ − z = 0 и изобразить их на комплексной плоскости, если

z = .

□ 1. a) Алгебраическая форма: z = a +ib.

Значит,

z = = =

= = = = = .

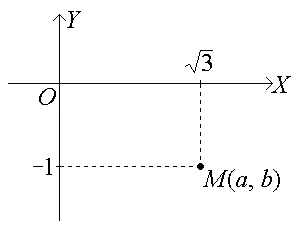
Следовательно,

z = a + ib = ,

где а = , b = −1,

.

б) Тригонометрическая форма:

z = ρ( + i ).

Значит,

ρ = = = 2,

φ = = = = .

Следовательно,

z = 2( + i( ).

Тригонометрическую форму комплексного числа можно найти другим способом:

z = = ( + i) =

= 2( + i) = 2( + i) = 2( + i( ).

в) Показательная форма: z = ρ e^iφ.

Так как ρ = 2, φ = , то z = 2 .

Изображение комплексного числа для пунктов а) и b):

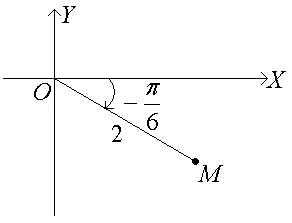
2. Так как комплексное число в алгебраической форме возводить в 10-ую степень сложно, то возведем в эту степень комплексное число в тригонометрической форме.

Так как zⁿ = ρⁿ( + i ), то

z¹⁰ = 2¹⁰( + i ) = 2¹⁰( + i ) =

= 2¹⁰( + i ).

В показательной форме:

так как zⁿ = ρⁿ , то z¹⁰ = 2¹⁰ = 2¹⁰ = 2¹⁰ .

Изображение полученного числа:

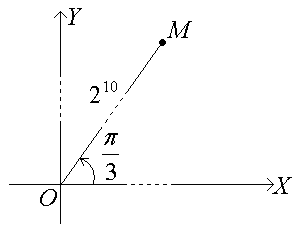
Из тригонометрической формы комплексного числа можно получить алгебраическую форму:

z¹⁰ = 2¹⁰( + i ) = 2¹⁰( + i ) = 2⁹ +2⁹ i,

где а = 2⁹, b = 2⁹ .

Тогда

.

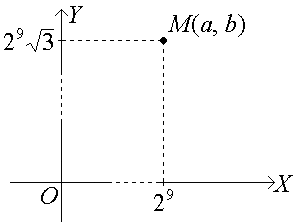3. Решим уравнение w³ − z = 0:

w³ = z, w = ,

т.е. необходимо найти все значения корня 3-ей степени из комплексного числа. Так как

= ( + i ),

где k = 0, 1, 2, …, n − 1, то

w = = = ( +

+ i ), где k = 0, 1, 2.

Тогда

k = 0: w₀ = ( + i );

k = 1: w₁ = ( + i );

k = 2: w₂ = ( + i ).

Все корни уравнения можно было найти, используя показательную форму комплексного числа. Так как

= = ,

где k = 0, 1, 2, …, n − 1, то

w = = = ,

где k = 0, 1, 2.

Тогда

k = 0: w₀ = ;

k = 1: w₁ = ;

k = 2: w₂ = .

Изображение полученных корней:

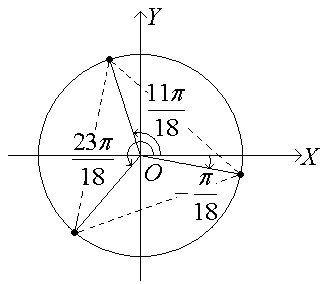
Точки, соответствующие значениям корней заданного уравнения, лежат в вершинах правильного треугольника, вписанного в окружность. Углы между радиусами этой окружности равны . ■