§ 5. Кривизна плоской кривой
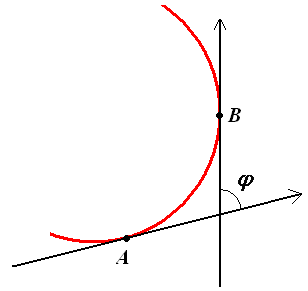
Углом смежности дуги АВ плоской кривой называется угол φ между касательными в точках А и В этой кривой.
Отношение угла
смежности к длине s
дуги АВ
называется средней
кривизной
дуги АВ,
т.е.
.
Кривизной
данной
кривой в точке А
называется предел средней кривизны
дуги АВ
при
,
т.е.
.
Кривизна
окружности
,
где а
– радиус окружности; кривизна прямой
равна нулю.
Если линия задана
уравнением
,
то ее кривизна вычисляется по формуле
.
Если кривая задана
параметрическими уравнениями
,
,
то
,
где
,
,
,
.
Если кривая задана
в полярных координатах уравнением
,
то
,
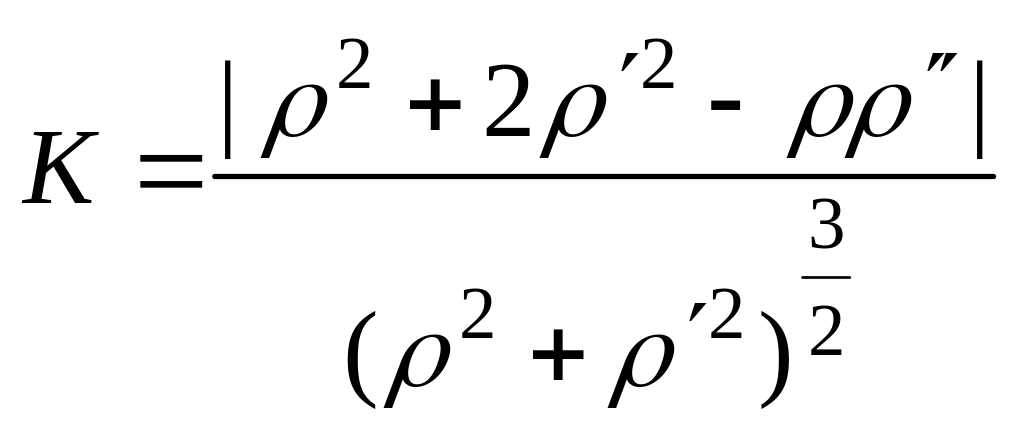где
,
.
Радиусом кривизны называется величина, обратная кривизне:
.
Окружностью
кривизны
данной линии в ее точке А
называется предельное положение
окружности, проходящей через три точки
А,
В,
С кривой,
когда
и
.
Радиус окружности кривизны равен радиусу кривизны. Центр окружности кривизны называется центром кривизны и находится на нормали к кривой, проведенной в точке А в сторону вогнутости этой линии.
Координаты
и
центра кривизны кривой
вычисляются по формулам
,
.
Эволютой линии называется множество ее центров кривизны. Формула для координат центра кривизны можно рассматривать как параметрические уравнения эволюты.
Пример.
Найти кривизну линии
в точке с абсциссой
.
□ Имеем
,
.
При
эти производные принимают значения
,
.
Тогда
=
=
=
.
■
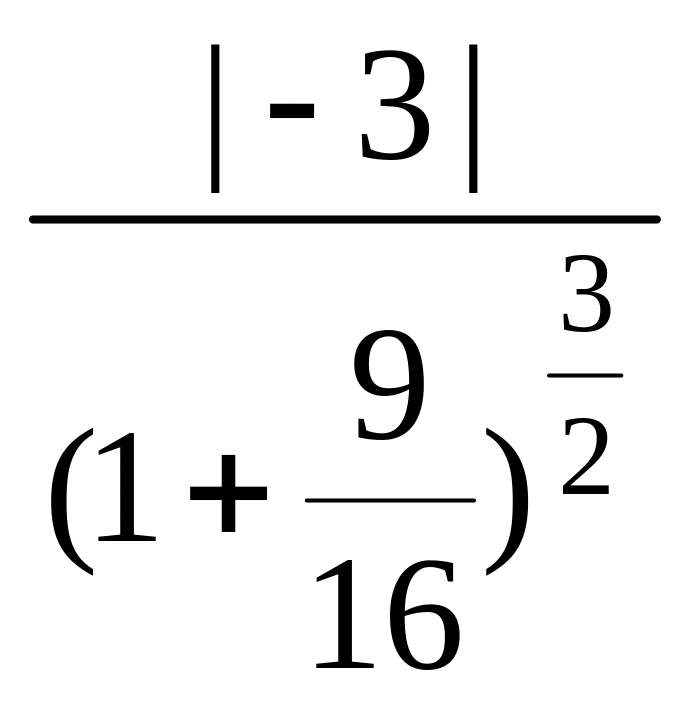Пример.
Найти кривизну в любой точке циклоиды
,
.
□ Имеем
,
,
,
,
=
,
=
,
.
■
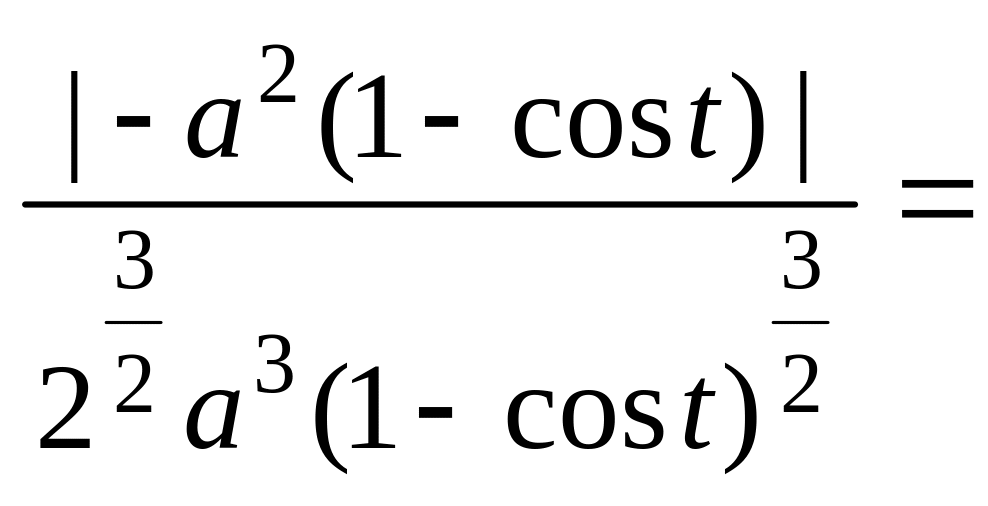
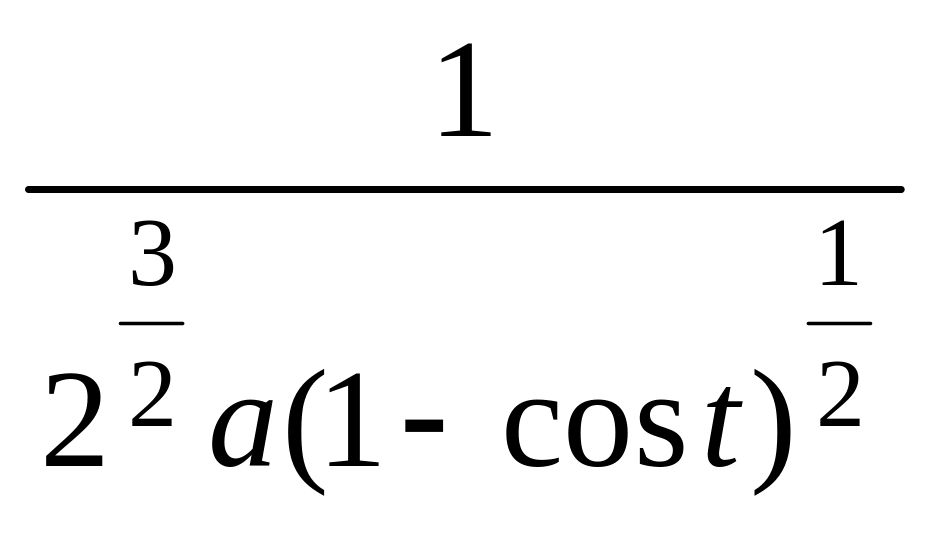Пример.
Найти координаты центра кривизны линии
в точке М(1;
1).
□ Продифференцируем уравнение данной кривой дважды:
(*),
(**).
Так
как х
= 1, у
= 1, то из уравнения (*) находим
,
а из уравнения (**) получаем
,
т.е
.
Тогда
=
,
,
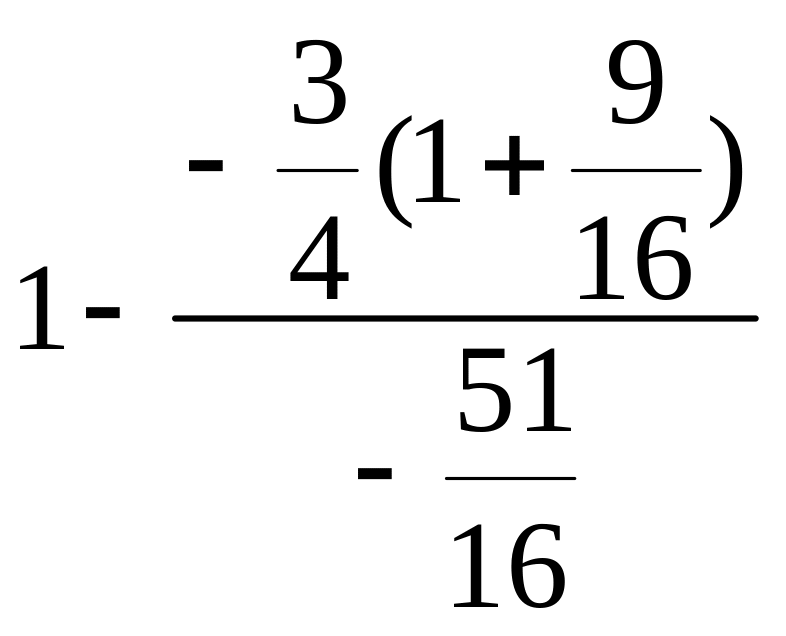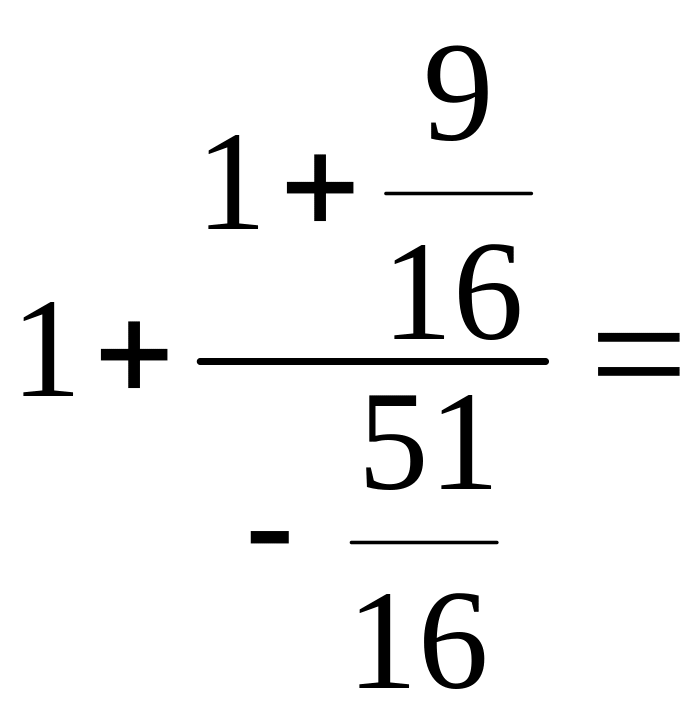
т.е.
.
■
Пример.
Составить уравнение эволюты параболы
.
□ Продифференцируем дважды уравнение параболы:
,
;
,
.
Определяем координаты центра кривизны:
;
.
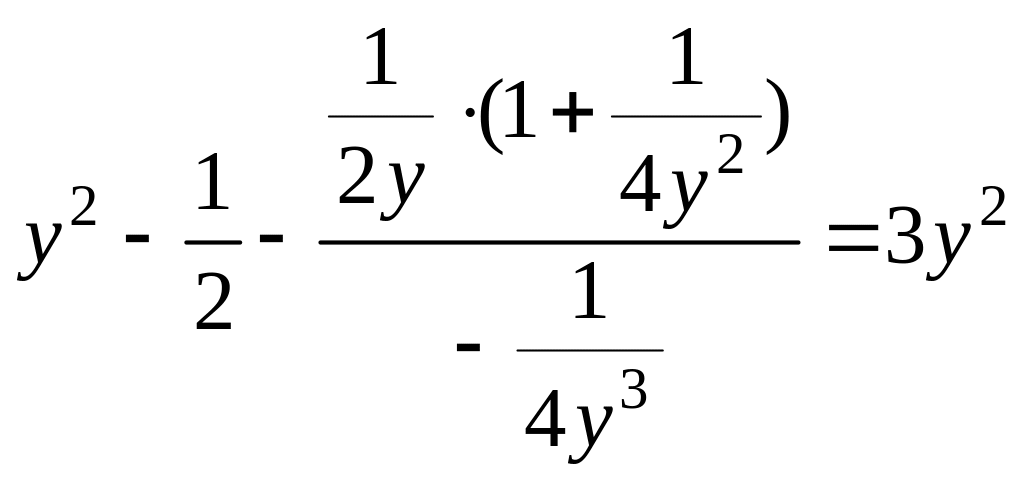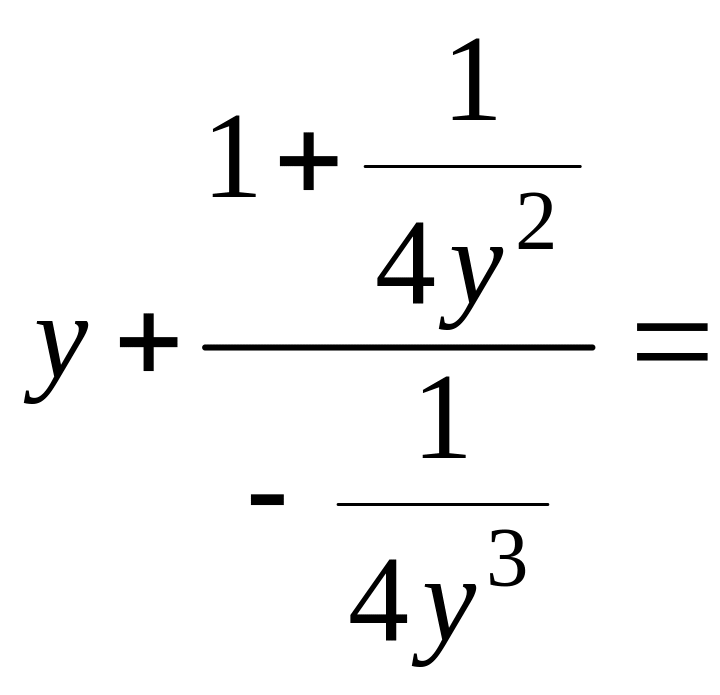
Получили
уравнение эволюты в параметрической
форме:
,
.
Исключая параметр у, найдем уравнение эволюты в явном виде:
.
■
Глава 4. Функции нескольких переменных
( ФНП )
§ 1. Основные понятия
Пусть имеется п переменных величин. Если каждому набору их значений (х1, х2,…, хп) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z, то говорят, что задана функция нескольких переменных
z = f(х1, х2,…, хп).
Функции двух и трех переменных принято записывать в виде:
z = f(х, y) и u = f(х, y, z).
Рассмотрим функцию z = f(х, y).
Совокупность пар (х, y) значений х и y, при которых определяется функция z = f(х, y), называется областью определения или областью существования этой функции.
Областью определения функции z = f(х, y) является плоскость ХОУ или часть этой плоскости, ограниченная линией.
Линию, ограничивающую указанную область, называют границей области.
Точки области, не лежащие на границе, называются внутренними точками области.
Область, состоящая из одних внутренних точек называется открытой или незамкнутой .
Если же к области относятся и точки границы, то область называется замкнутой.
Область называется ограниченной, если существует такая постоянная С, что расстояние от любой точки М области до начала координат О (0,0) меньше С, т.е. |ОМ| < C.
Пример. Найти область определения функции
z = 2х − y.
□ Аналитическое выражение 2х − y имеет смысл при любых значения х и y. Следовательно, областью определения функции z = 2х − y является вся плоскость ХОУ. ■
Пример. Найти область определения функции
z
=
.
□ Подкоренное выражение должно быть неотрицательным:
1
− х2
− у2
0.
Отсюда
следует х2
+ у2
1. Следовательно, областью определения
заданной функции является часть плоскости
ХОY,
представляющая собой круг с границей
(окружность):
■
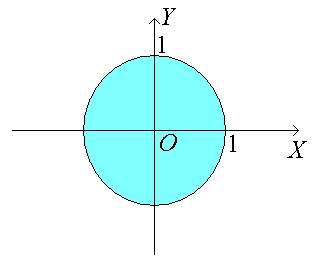Областью определения функции трех переменных u = f(х, y, z) является некоторая совокупность точек пространства, т.е. все пространство или его часть.
Область определения функции четырех и более переменных уже не допускает простого геометрического истолкования.
Рассмотрим функцию
z = f(х, y). (1)
Геометрическое место точек, координаты которых удовлетворяют уравнению (1), называется графиком этой функции.
Графиком функции z = f(х, y) является некоторая поверхность в трехмерном пространстве, проектирующаяся на плоскость ХОУ в область определения этой функции.
Каждый перпендикуляр к плоскости ХОУ пересекает поверхность z = f(х, y) не более чем в одной точке.
Пример. □ Рассмотрим сферу
(х – а)2 + (у – b)2 + (z – c)2 = R2
с
центром в точке
(a,
b,
c).
Преобразуем это уравнение:
z
=
+ c.
В результате получили две функции от двух переменных. Рассмотрим одну из них, например
z
=
+ c.
Графиком этой функции является поверхность – полусфера:
■
Функцию трех и более переменных изобразить с помощью графика в пространстве невозможно.
Рассмотрим функцию z = f(х, y).
Пусть у сохраняет постоянное значение; дадим независимой переменной х приращение . Тогда функция z получит приращение
− f(х,
y)
− частное
приращение функции
z
по
х.
Пусть х сохраняет постоянное значение; дадим независимой переменной у приращение . Тогда функция z получит приращение
− f(х,
y)
− частное
приращение функции
z
по
у.
Если дать х приращение , а у приращение , то функция z получит приращение
− f(х,
y)
− полное
приращение функции
z
.
В общем случае
+
.
Пример. Найти приращения функции
z = хy.
□ Имеем
− ху
= ху
+ у
− ху
= у
;
− ху
= ху
+
− ху =
;
− ху
= ху
+
+ у
+
− ху
=
+ у
+
+ .
Видно, что + . ■
Аналогично определяются частные и полные приращения функции любого числа переменных.