§ 8. Непрерывность функции на отрезке

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна в каждой точке этого отрезка. Причем на конце а отрезка f(x) непрерывна справа, т.е. = f(а), а на конце b функция f(x) непрерывна слева, т.е. = f(b)

Замечание. Любая элементарная функция непрерывна в своей области определения.

Основные свойства функций, непрерывных на отрезке

1⁰. Прохождение непрерывных функций через любое промежуточное значение.

Теорема 1. (1-я теорема Больцано − Коши).

Пусть функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает значения разных знаков. Тогда (а, b), в которой f( ) = 0.

Геометрический смысл:

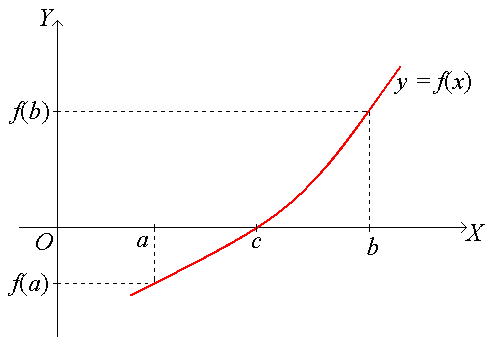
Если функция f(x) принимает на концах отрезка значения разных знаков, то ее график обязательно пересечет ось ОХ в некоторой точке х = , в которой f( ) = 0.

Теорема 2. (2-я теорема Больцано − Коши).

Пусть функция f(x) непрерывна на отрезке [a, b] и пусть f(а) = А, f(b) = . Пусть – любое число, заключенное между А и . Тогда [а, b], в которой f( ) = .

Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения.

○ Пусть для определенности А < и А < < :

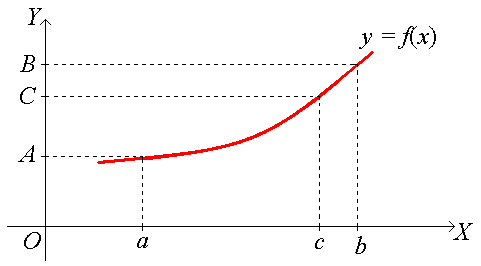
Рассмотрим вспомогательную функцию φ(x) = f(x) − . Функция φ(x) непрерывна на отрезке [а, b] и принимает значения разных знаков на концах [а, b]:

φ(а) = f(а) − = А – < 0,

φ(b) = f(b) − = – > 0.

Согласно теореме 1 (а, b), что φ( ) = f( ) − = 0, т.е. f( ) = . ●

Следствие. Если f(x) определена и непрерывна на некотором промежутке Х, то множество ее значений Y также представляет некоторый промежуток.

2⁰. Ограниченность непрерывной функции.

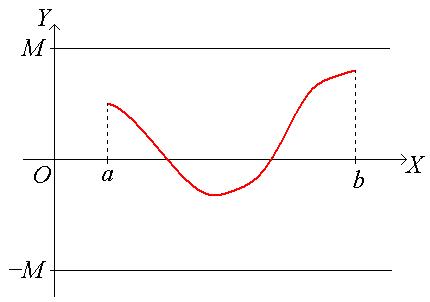
Функция f(x) называется ограниченной на отрезке [а, b], если М > 0 такое, что для х [а, b] выполняется неравенство | f(x)| ≤ M или −М ≤ f(x) ≤ М.

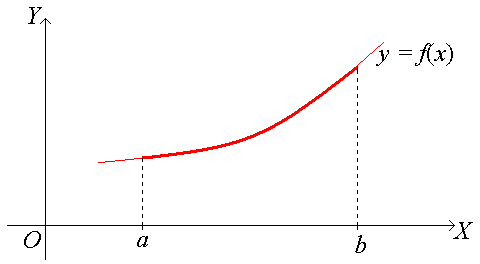
Другими словами, график функции f(x) не выходит из полосы, ограниченной прямыми у = М и у = −М:

Теорема 3. (1-я теорема Вейерштрасса).

Если f(x) определена и непрерывна на [а, b], то она ограничена на этом отрезке.

3⁰. Максимальное и минимальное значения функции на отрезке.

Теорема 4. (2-я теорема Вейерштрасса).

Если f(x) непрерывна на [а, b], то она достигает на этом отрезке своих точных граней, т.е. х₁, х₂ [а, b] такие, что

f(x₁)= М = , f(x₂)= т = .

(supremum (лат.) – наивысшее; infinum (лат.) – наинизшее).

○

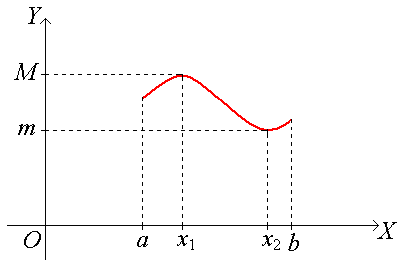
Так как f(x) непрерывна на [а, b], то она ограничена. Следовательно, существуют точная верхняя М и точная нижняя т грани функции f(x) на отрезке [а, b].

Покажем, что х₁ [а, b], такая, что f(x₁) = М. Рассуждаем от противного. Пусть f(x) не принимает ни в одной точке [а, b] значения, равного М. Тогда для х [а, b] справедливо неравенство f(x) < М.

Рассмотрим вспомогательную, всюду положительную функцию

F(x) = .

Функция F(x) непрерывна как частное непрерывных функций, а значит, ограничена, т.е. μ > 0 такое, что для х [а, b]

F(x) = ≤ μ,

откуда

f(x) ≤ М − .

Получили, что число М − < M и является верхней гранью f(x) на отрезке [а, b]. Но это противоречит тому, что число М – точная верхняя грань функции f(x) на отрезке [а, b]. Полученное противоречие и доказывает, что х₁ [а, b], в которой f(x₁) = М.

Аналогично доказывается, что f(x) достигает на [а, b] своей точной нижней грани т. ●

Замечание. Точная верхняя грань – максимальное значение функции f(x) на отрезке [а, b]; точная нижняя грань – минимальное значение функции f(x) на отрезке [а, b].

Непрерывность обратной функции

Функция f(x) называется неубывающей (невозрастающей) на промежутке Х, если для х₁,х₂ Х, х₁< х₂, справедливо неравенство f(x₁) ≤ f(x₂) (f(x₁) ≥ f(x₂)).

Неубывающие и невозрастающие функции объединяют общим названием монотонные функции.

Если для х₁,х₂ Х, х₁< х₂, справедливо неравенство f(x₁) < f(x₂) (f(x₁) > f(x₂)), то функция f(x) называется возрастающей (убывающей) на промежутке Х.

Возрастающие и убывающие функции называют также строго монотонными.

Теорема. Пусть функция у = f(x) определена, строго монотонна и непрерывна на некотором промежутке Х, и пусть Y – множество ее значений. Тогда на множестве Y обратная функция х = φ(у) однозначна, строго монотонна и непрерывна.

Замечание. Если обратная функция х = φ(у) однозначная, то, очевидно, функция у = f(x) является обратной для функции х = φ(у). Такие функции называются взаимно обратными (взаимно однозначными).

Обратная функция х = φ(у) находится путем решения уравнения у = f(x) относительно х.

Если у = f(x) не является ни возрастающей, ни убывающей на некотором промежутке, то она может иметь несколько обратных функций.

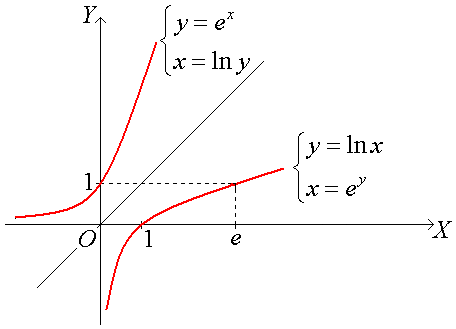
Если функции у = f(x) и х = φ(у) являются взаимно обратными, то графиками их является одна и та же кривая. Но, если аргумент обратной функции мы обозначим снова через х, а функцию через у и построим графики в одной координатной системе, то получим уже два различных графика. При этом графики будут симметричны относительно биссектрисы первого и третьего координатных углов: