§ 18. Правило лопиталя

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, т.е. если имеется неопределенность вида или , то

= . (1)

○ Пусть для определенности имеется неопределенность при х → х₀. Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке х₀, причем

= f(x₀) = 0,

= g(x₀) = 0.

В этом случае

= .

Применяя теорему Лагранжа для функций f(x) и g(x) на отрезке [x, x₀], получим

= = ,

где х < c₁ < x₀, х < c₂ < x₀.

При х → х₀ в силу непрерывности производных и имеем

→ , → .

Используя теорему о пределе частного двух функций получаем равенство (1). ●

Замечание 1. Правило Лопиталя справедливо и в случае, когда

х →х₀+, х →х₀−, х →+∞, х →−∞, х →∞.

Замечание 2. При необходимости правило Лопиталя можно использовать требуемое число раз.

Раскрытие неопределенностей

а) Неопределенности вида , .

В этом случае используется правило Лопиталя.

Пример. Найти предел

.

□ Имеем

= = = = = =

= · = ·1 = . ■

Неопределенности вида , .

Данные неопределенности сводятся к неопределенностям , .

Пример. Найти предел

.

□ Имеем

= = = = = =

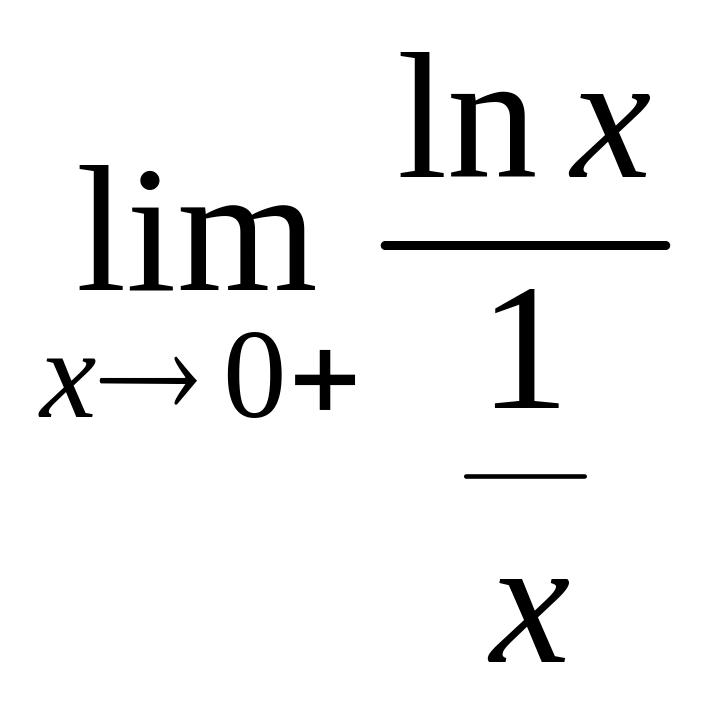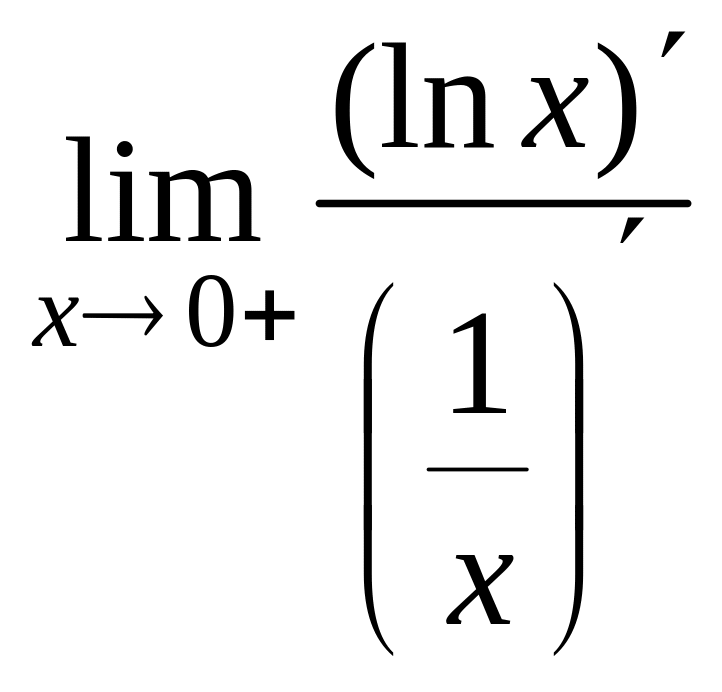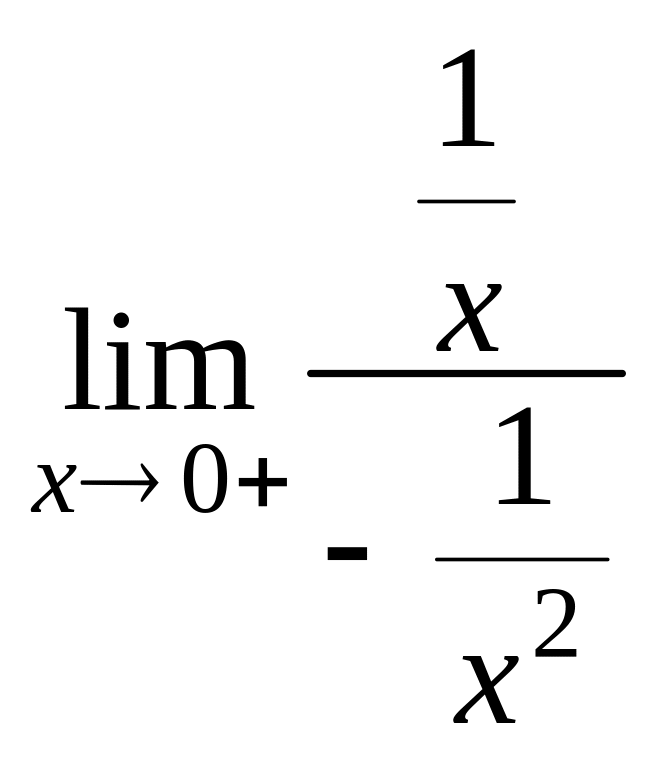= − = 0. ■

Пример. Найти предел

.

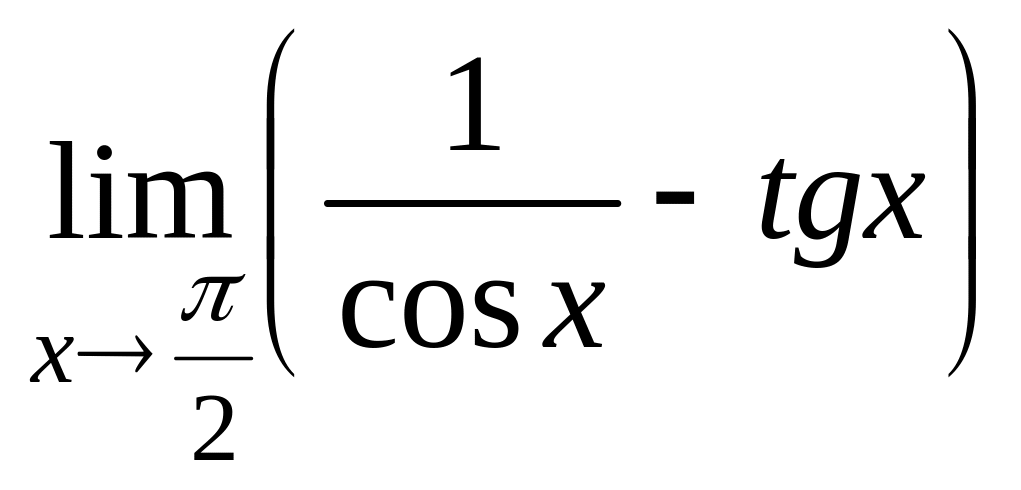□ Имеем

= = = = =

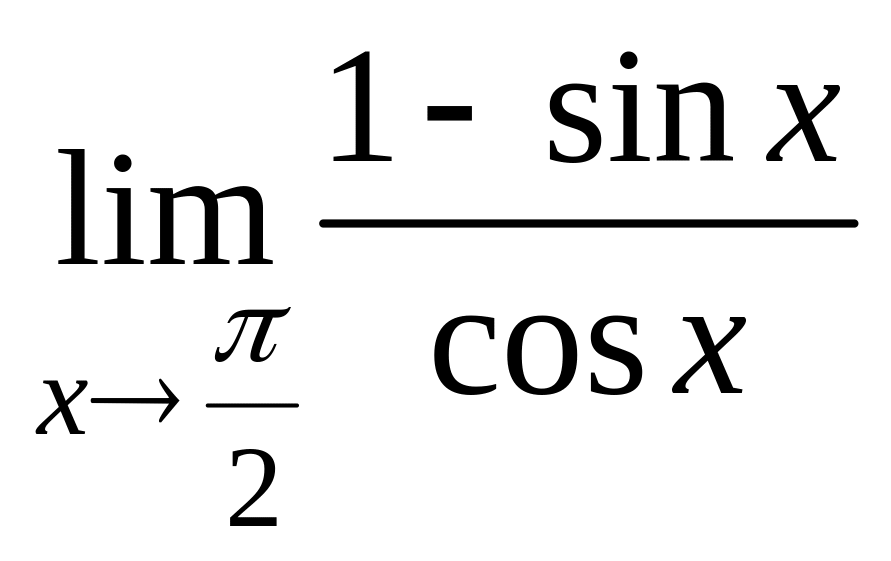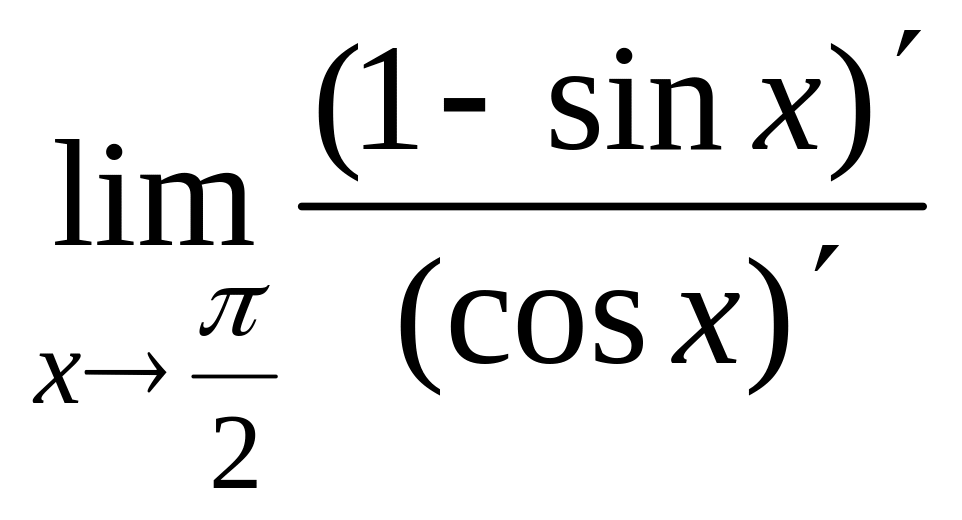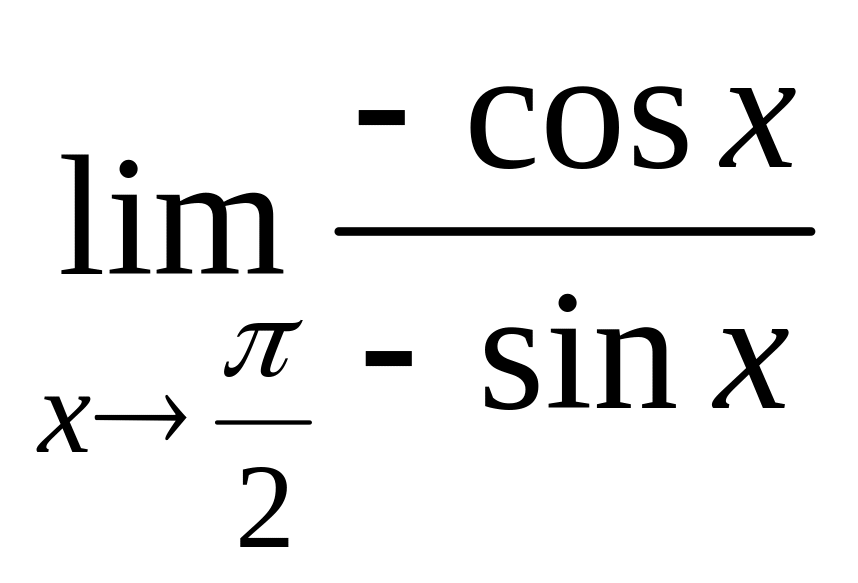= = 0. ■

Неопределенности вида , , .

Такие неопределенности встречаются при рассмотрении показательно-степенных функций у = , где и = и(х), v = v(x).

Эти неопределенности с помощью тождества

= =

сводятся к неопределенности .

Пример. Найти предел

.

□ Имеем

= = = = !

= = = = = =

= − = 0.

! = е⁰ = 1. ■

Замечание. Правило Лопиталя не всегда приводит к конечному результату.

Пример. Найти предел

.

□ Имеем

= = = .

Этот предел не существует, т.е. правило Лопиталя не дает ответа.

Найдем предел другим способом:

= = = = 1 + 0 = 1. ■

§ 19. Уравнения касательной и нормали к кривой

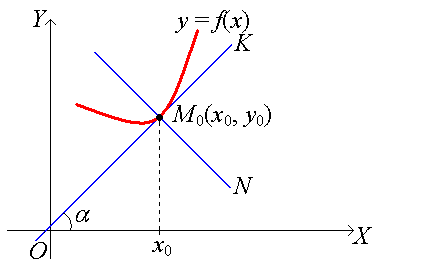
Из аналитической геометрии известно уравнение прямой, проходящей заданную точку М₀(х₀, у₀):

у − у₀ = k(x − x₀),

где k = − угловой коэффициент.

Из геометрического смысла производной следует, что = . Тогда уравнение

у − у₀ = (x − x₀)

является уравнением касательной К к кривой у = f(x) в точке х₀.

Так как касательная К и нормаль N взаимно перпендикулярны, то уравнение

у − у₀ = (x − x₀)

является уравнением нормали N к кривой у = f(x) в точке х₀.

Пример. Составить уравнения касательной и нормали к кривой

у =

в точке х = 2.

□ Уравнение касательной имеет вид

у − у₀ = (x − x₀).

Имеем x₀ = 2, у₀ = = 1, т.е. М₀ = (2; 1).

Найдем производную

= 8 = − . Тогда = = − =

= − .

Подставляем в уравнение касательной:

у − 1 = − (x − 2), 2у − 2 = − x + 2

или

х + 2у – 4 = 0.

Уравнение нормали:

у − у₀ = (x − x₀).

Подставляя значения, получим

у − 1 = 2(x − 2), у − 1 = 2x − 4

или

2х – у – 3 = 0. ■