§ 2. Непрерывность и производная векторной функции скалярного аргумента

Рассмотрим векторную функцию скалярного аргумента t и выберем произвольное, но определенное значение t этого аргумента.

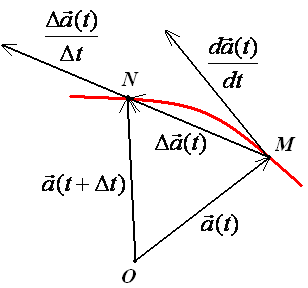
Вектор, соответствующий выбранному значению t :

.

Давая аргументу приращение , получим другой вектор:

.

Вектор получается из вектора прибавлением к последнему вектора . Поэтому вектор является приращением вектора , т.е

.

Так как , то .

Известно, что проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. Поэтому

,

где

,

,

.

Кроме того

. (1)

Векторную функцию называют непрерывной при данном значении аргумента t, если модуль ее приращения стремится к нулю при :

.

Чтобы найти предел векторной функции при , достаточно найти пределы трех ее проекций на оси координат:

. (2)

Для двух векторов и справедливо неравенство

.

Следовательно,

.

Отсюда можно заключить, что непрерывность векторной функции влечет за собой непрерывность ее модуля. Обратное предположение является неверным.

Отметим, что годографом непрерывной векторной функции скалярного аргумента является непрерывная кривая.

Можно показать, что сумма, разность, скалярное и векторное произведения двух непрерывных векторных функций, а также произведение непрерывной векторной функции на непрерывную скалярную являются непрерывными функциями.

Составим для непрерывной векторной функции отношение и перейдем к пределу при .

Производной векторной функции называется предел

,

если он существует.

Производная есть векторная функция того же скалярного аргумента t.

Производная от векторной функции скалярного аргумента t лежит на касательной к годографу и направлена в сторону возрастания аргумента.

В проекциях:

.

На основании формулы (2) можно написать

, (3)

где

, , −

производные скалярных функций по аргументу t.

Модуль производной вектора равен

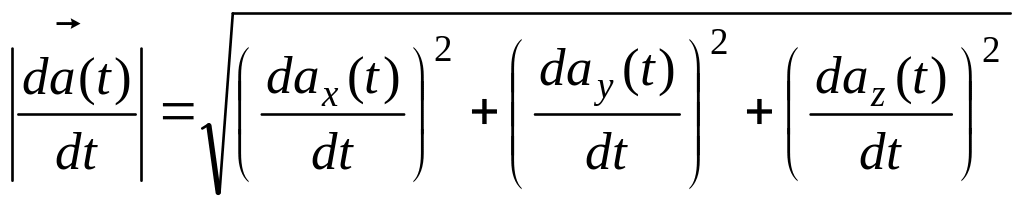. (4)

Механический смысл.

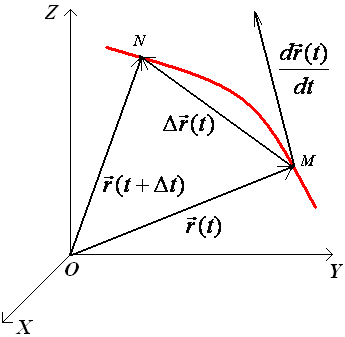
Пусть материальная точка движется по траектории, уравнение которой в проекциях имеет вид:

,

где − уравнения траектории в параметрической форме, t − время.

Тогда вектор = изображает перемещение точки за время , а отношение дает среднюю скорость перемещения за этот промежуток времени. Переходя к пределу при , из вектора средней скорости получим вектор мгновенной скорости в момент времени t. Следовательно, вектор скорости есть производная радиуса-вектора движущейся точки по времени:

= . (5)

Его модуль

.

С другой стороны, известно, что производная от длины кривой s по параметру t также выражается формулой

.

Таким образом, численное значение (модуль) вектора скорости равно производной от длины дуги траектории по времени:

. (6)

Дифференцируя вектор два раза, получим вектор ускорения :

. (7)

Его модуль

.
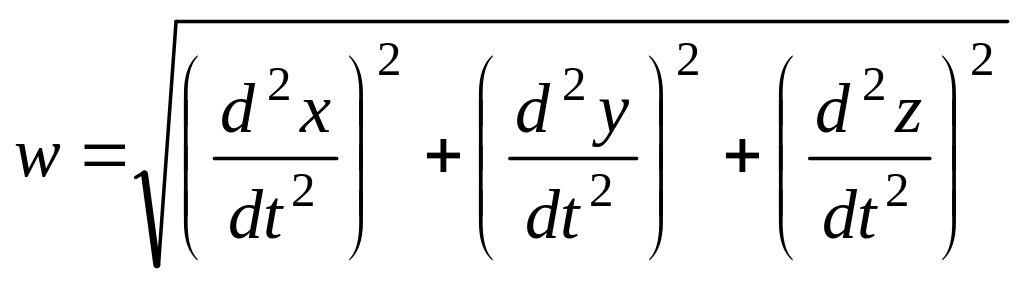