§ 2. Предел функции

Рассмотрим функцию z = f(х, y).

Окрестностью радиуса r точки М₀(х₀,у₀) называется совокупность точек (х, y), удовлетворяющих неравенству < r, т.е. совокупность точек, лежащих внутри круга радиуса r с центром в точке М₀(х₀, у₀).

Пусть дана функция z = f(х, y), определенная в некоторой области плоскости ХОУ. Рассмотрим некоторую определенную точку М₀(х₀, у₀), лежащую в этой области или на ее границе.

Число А называется пределом функции z = f(х, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для > 0, найдется такое число r > 0, что для всех точек М(х, у), для которых выполняется неравенство |MM₀| < r имеет место неравенство

| f(х, y) − A| < .

Обозначение: = А.

Пример. Найти предел

.

□ Имеем

= = =

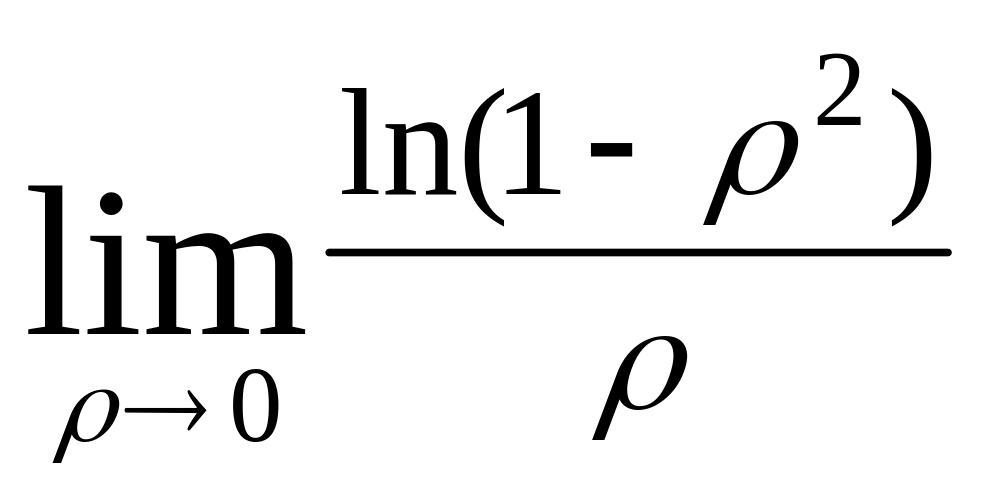= = = 0. ■

В общем случае нахождение пределов функции нескольких переменных весьма трудоемкая задача.

§ 3. Непрерывность функции

Рассмотрим функцию z = f(х, y).

Пусть точка М₀(х₀, у₀) из области определения функции z = f(х, y).

Определение 1. Функция z = f(х, y) называется непрерывной в точке М₀(х₀, у₀), если

= f(х₀, y₀).

Причем точка М(х, у) может стремиться к точке М₀(х₀, у₀) произвольным образом, оставаясь в области определения функции.

Определение 2. Функция z = f(х, y) называется непрерывной в точке М₀(х₀, у₀), если

, т.е. = 0.

Обозначим . Если и , то . Тогда последнее равенство можно записать в виде

= 0.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.

Если в некоторой точке N(х₀, у₀) не выполняются условия непрерывности, то точка N(х₀, у₀) – точка разрыва функции z = f(х, y).

Пример. Показать, что функция z = x² + y² непрерывна при любых значениях х и у, т.е. в любой точке плоскости ХОУ.

□ Найдем полное приращение функции z :

∆z = ((x + ∆x)² + (y + ∆y)²) – (x² + y²) = = 2x∆x + 2y∆y + ∆x² + ∆y².

Найдем предел:

. ■

Свойства непрерывной функции в замкнутой и ограниченной области

1⁰. Если функция f(x, y) определена и непрерывна в замкнутой и ограниченной области D, то в области D найдется по крайней мере одна точка N(х₀, у₀) такая, что для всех других точек области будет выполняться неравенство

f(x₀, y₀) f(x, y),

и по крайней мере одна точка такая, что для всех других точек области будет выполняться неравенство

f f (х, у).

Значение функции f(х₀, у₀) = М называется наибольшим значением функции f(x, y) в области D, а значение f = m – наименьшим значением.

2⁰. Если f(x, y) непрерывна в замкнутой и ограниченной области D и если M и m – наибольшее и наименьшее значения функции f(x, y) в области, то для любого числа А, удовлетворяющего условию

m < А < М, найдется в области точка N^*(x₀^*, y₀^*), что будет выполняться равенство f(x₀^*, y₀^*) = A.

Следствие. Если функция f(x, y) непрерывна в замкнутой и ограниченной области D и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых f(x, y) = 0.

Указанные свойства можно распространить на функции большего числа переменных.