§ 7. Непрерывность функции в точке

Определение 1. Функция f(x) называется непрерывной в точке х₀, если:

1. она определена в точке х₀ (т.е. существует значение f(x₀));

2. она имеет конечный предел х →х₀;

3. этот предел равен значению функции в точке х₀, т.е.

= f(x₀).

На практике часто используют другую запись:

= = f(x₀),

т.к.

= А, если = = А.

Если

= f(x₀) ( = f(x₀)),

то функцию f(x) называют непрерывной в точке х₀ справа (слева). Если функция f(x) непрерывна в точке х₀ и справа и слева, то она непрерывна в точке х₀.

Пример. Доказать непрерывность функции f(x) = 3х² + 2х + 1 в точке х₀ = 1.

□ Функция определена в точке х₀ = 1:

f(1) = 3∙1² + 2∙1 + 1 = 3 + 2 + 1 = 6.

Существует конечный предел при х → 1:

= 3 + 2 + 1 = 6.

Видно, что предел функции при х →1 равен значению функции в точке х₀ = 1:

= f(1) = 6.

Следовательно, по определению 1 заданная функция непрерывна точке х₀ = 1. ■

Пусть функция у = f(x) определена при некотором значении х₀ и в некоторой окрестности с центром в точке х₀. Пусть у₀ = f(x₀).

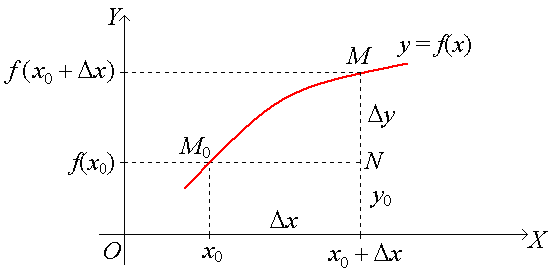
Если аргумент х получит некоторое положительное (или отрицательное) приращение Δх и примет значение х₀ + Δх, то функция у получит некоторое приращение Δу. Новое значение функции будет у₀ + Δу = f(x₀ + Δх). Тогда приращение функции можно записать в виде

Δу = f(x₀ + Δх) − f(x₀).

Определение 2. Функция f(x) называется непрерывной в точке х₀, если она определена в этой точке и в некоторой ее окрестности, и

= 0

или

= 0.

Последнее выражение можно записать в виде:

= f(x₀)

или

= f(x₀),

но

x₀ = .

Следовательно, можно записать

= f( ),

т.е. для того, чтобы найти предел непрерывной функции при х →х₀, достаточно в выражение функции подставить вместо аргумента х его значение x₀.

Пример. Доказать, что функция f(x) = х² непрерывная в любой точке x₀.

□ Воспользуемся 2-м определением:

= 0.

Имеем

Δу = f(x₀ + Δх) − f(x₀) = (x₀ + Δх)² − x₀² = x₀² + 2x₀Δх + (Δх)² − x₀² =

= 2x₀Δх + (Δх)².

Тогда

= = 0.

Так как точка x₀ произвольная, то доказано, что заданная функция непрерывна в любой точке. ■

Пример. Доказать, что функция f(x) = непрерывная в любой точке x₀.

□ Воспользуемся 2-м определением:

= 0.

Имеем

Δу = f(x₀ + Δх) − f(x₀) = (x₀ + Δх) − x₀ = 2 (x₀ + ).

Тогда

= 2 (x₀ + ) = 0.

Следовательно, функция непрерывна в любой точке x₀. ■

Арифметические действия над непрерывными функциями:

Пусть функции f(x) и g(x) непрерывны в точке x₀. Тогда функции f(x) ± g(x), f(x)∙g(x) и (g(x) ≠ 0) также непрерывны в этой точке.

Определение и классификация точек разрыва функции

Точка x₀ называется точкой разрыва функции f(x), если f(x) в этой точке не является непрерывной.

Разрывы функций классифицируются следующим образом.

Точка x₀ называется точкой разрыва 1-го рода функции f(x), если одновременно не равны друг другу три числа:

, , f(x₀)

или

f(x₀ + 0), f(x₀ − 0), f(x₀).

Точки разрыва 1-го рода делятся:

1. точки устранимого разрыва, когда

= ≠ f(x₀)

или

f(x₀ + 0) = f(x₀ − 0) ≠ f(x₀);

2. точки скачка, когда

≠

или

f(x₀ + 0) ≠ f(x₀ − 0).

Разность | − | или | f(x₀ + 0) − f(x₀ − 0)| называют скачком функции f(x) в точке x₀.

Точка x₀ называется точкой разрыва 2-го рода функции f(x), если в этой точке f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Исследовать функцию на непрерывность в указанных точках. Сделать рисунок.

□ Для исследования непрерывности воспользуемся выражением

. (*)

Пусть х₀ = х₁ = 0, тогда

;

;

.

Пределы слева и справа равны между собой и совпадают со значением функции в точке х₀ = 0, т.е. выражение (*) выполняется. Следовательно, заданная функция непрерывна в этой точке.

Пусть х₀ = х₂ = 2, тогда

функция не определена.

Так как левый предел бесконечен, то заданная функция в этой точке терпит бесконечный разрыв.

Точка х₂ = 2 – точка разрыва 2-го рода.

Для построения графика следует найти еще два предела:

;

.

Построим рисунок :

■

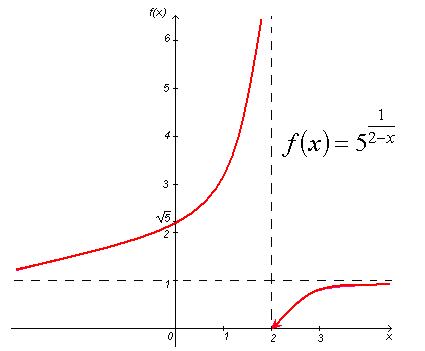Непрерывность сложной функции

Теорема. Пусть функция z = φ(х) непрерывна в точке х₀, а функция у = f(z) непрерывна в точке z₀ = φ(х₀). Тогда сложная функция у = f(φ(х)) непрерывна в точке х₀.

○ Из определения непрерывности функции z = φ(х) в точке х₀ следует, что она определена в некоторой окрестности этой точки. Возьмем из этой окрестности любую последовательность точек

х₁, х₂, …, х_п, …,

сходящуюся к точке х₀. Тогда, в силу непрерывности функции z = φ(х) в точке х₀, имеем

= = φ(х₀) = z₀,

т.е. соответствующая последовательность точек z₁, z₂, …, z_п, … сходится к точке z₀. В силу же непрерывности функции f(z) в точке z₀, получаем

= f(z₀),

т.е.

= f(φ(х₀)).

Следовательно, предел функции f(φ(х)) в точке х₀ равен ее значению в этой точке, что и доказывает непрерывность сложной функции f(φ(х)) в точке х₀. ●

Пример. Доказать непрерывность сложной функции у = в точке х = 0.

□ Заданную сложную функцию можно записать в виде у = , где z = х². Так как функция z = х² непрерывна в точке х = 0, а функция у = непрерывна в точке z = 0, то по доказанной теореме сложная функция у = непрерывна в точке х = 0. ■