§ 17. Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Пусть функция
определена и непрерывна в граниченной
замкнутой области
.
Тогшда в области
она достигает своих наименьшего и
наибольшего значений, причем эти значения
достигаются либо внутри области
,
либо на границе области
.
Точки, в которых функция принимает наибольшее и наименьшее значения в ограниченной замкнутой области, называют точками абсолютного или глобального экстремума .
Чтобы найти наибольшее и наименьшее значения функции в ограниченной замкнутой области , следует вычислить значения функции в критических точках области , а также наибольшее и наименьшее значения на ее границе. Из найденных значений выбрать требуемые.
Пример. Найти наибольшее и наименьшее значения функции
в
замкнутой области
,
ограниченной осью
,
прямой
и параболой
при
.
□
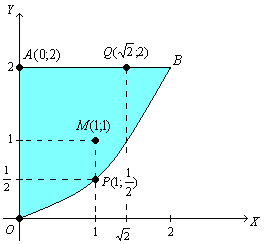
Определим критические точки внутри области :
,
,
,
,
Получили
две точки
,
.
Исследуем функцию на границе области.
Отрезок
:
,
,
;
,
,
;
на отрезке
:
Значит, на
функция возрастает. Наибольшее и
наименьшее значения она принимает на
концах отрезка
:
,
.
Отрезок
:
,
,
;
,
,
.
Нас интересует только точка из
,
т.е.
Таким
образом, получаем точку
.
Дуга параболы
:
,
,
;
,
,
,
,
.
Оба значения удовлетворяют неравенствам
.
Найдем ординаты этих точек:
=
0,
.
В результате получим две точки
,
.
Вычисляем значения функции в найденных точках:
=
,
,
,
,
.
Выбираем из найденных значений функции наибольшее и наименьшее значения:
,
.
■
Литература
1. Бугров Я.М., Никольский С.М. Дифференциальное и интегральное
исчисление. Учебное пособие для вузов. -М.: Наука, 1988.-432с
2. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1.– М.: Наука, 1985. – 452 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.2. –
М.: Наука, 1985.- 506с.
4. Шипачев В.С. Основы высшей математики. – М.: Высш. шк., 1989. –
479 с.
5. Герасимович А.И., Рысюк Н.А. Математический анализ. Справ.
пособие в 2 ч. Ч.1. -Мн.: Высш. шк., 1989.-287с
6. Герасимович А.И., Кеда Н.А., Сугак М.Б. Математический анализ.
Справ. пособие в 2 ч. Ч.2. -Мн.: Высш. шк., 1990.-272с.
7. Гольдфайн И.А. Векторный анализ и теория поля. − М.: Физматгиз,
1962. − 132 с.
8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в уп- ражнениях и задачах. Ч.1. – М.: Высшая школа, 1986. – 304 с.
Электронное пособие
КУРС ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
(Дифференциальное исчисление).
Для студентов дневной и заочной форм обучения
направления подготовки 6.050102
«Компьютерная инженерия»
Составитель:
Александр Евгеньевич Богданов
Редактор А.Е. Богданов
Техн. редактор Л.А. Лыгина
Оригинал – макет Л.А. Лыгина
Підписано до друку ____________
Формат
.
Папір типограф. Гарнітура Times.
Друк офсетний. Ум. друк. арк.___. Обл.-вид.арк._____.
Тираж ___ прим. Вид. №_______. Замова №______. Ціна договірна.
Видавництво Технологічного інституту
СНУ ім. Володимира Даля(м. Сєвєродонецьк)
Адреса видавництва: 93400, м. Сєвєродонецьк, Луганської обл.,
пр. Радянський, 59-а, головний корпус
Телефон: 8(06452) 4-03-42
E-mail: sti@sti.lg.ua