§ 3. Правила дифференцирования. Дифференциал. Производная единичного вектора
Напишем основные правила дифференцирования векторных функций.
1.
,
− постоянный вектор;
2.
;
3.
,
где т
= т(t)
− скалярная функция;
4
;
5.
.
Пример. Найти производную скалярного произведения векторов
и
.
□ Имеем
+
=
= −6 + 6 = 0.
Полученный
результат объясняется тем, что скалярное
произведение заданных векторов
,
т.е. является постоянной величиной.
■
По аналогии с
дифференциалом скалярной функции
дифференциал векторной функции
есть вектор
,
определяемы равенством
,
где
− приращение скалярного аргумента t.
Дифференциал
вектора
,
как и производная
вектора
,
лежит на касательной к годографу.
Направление
на этой касательной зависит от знака
:
при
вектор
направлен в сторону возрастания
аргумента t,
при
,
наоборот, в сторону его убывания.
Дифференциал векторной функции в проекциях:
или
,
где
− дифференциалы скалярных функций
.
Модуль дифференциала векторной функции :
.
В
частности, для дифференциала радиус-вектора
точки
и его модуля имеем
и
.
С
другой стороны, дифференциал длины дуги
кривой
определяется формулой
.
Следовательно,
,
т.е. модуль дифференциала радиус-вектора точки равен дифференциалу длины дуги, описываемой этой точкой.
Рассмотрим единичный
вектор
,
изменяющийся при изменении скаляра t
только по направлению. В этом случае
и
модуль вектора приращения
определяется из равенства
,
где
− угол смежности векторов
и
.
Отсюда следует, что
.
Рассматривая
аргумент t
как время, можно интерпретировать
производную
как угловую скорость вращения единичного
вектора.
Производная от единичного вектора есть вектор, перпендикулярный к нему, модуль которого равен угловой скорости вращения.
Отсюда следует, что производная единичного вектора, вообще говоря, не есть единичный вектор; она будет таковым, если вращение первоначального вектора происходит равномерно.
Пусть векторная
функция
скалярного аргумента t
изменяется как по величине, так и по
направлению. Вектор
можно представить как произведение его
модуля
и единичного вектора его направления
:
.
Тогда
.
Вектор
,
как производная единичного вектора,
перпендикулярен вектору
и тем самым вектору
.
Следовательно, первое слагаемое
есть вектор, перпендикулярный вектору
,
а слагаемое
− вектор, ему параллельный. Таким
образом, последняя формула дает разложение
производной
от вектора
по направлению первоначального вектора
и к нему перпендикулярному.
Когда вектор
изменяется только по модулю, то вектор
сохраняет постоянное направление и
= 0. Если же вектор
имеет постоянный модуль, то
= 0. В этом случае
образует с вектором
прямой угол.
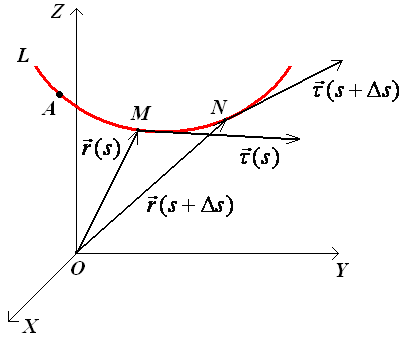
§ 4. Некоторые приложения векторных функций скаляроного аргумента
Пусть точка М(х,
y,
z)
описывает кривую L
в пространстве. Параметром, определяющим
положение точки М
на кривой, будем считать длину s
дуги АМ
кривой, отсчитываемую от определенной
точки А
кривой до точки М.
Радиус-вектор
точки М
будет функцией скалярного аргумента
s:
.
В проекциях радиус-вектор точки запишется как
,
где
− скалярные функции длины дуги s.
При этом величина s
считается положительной, если она
отложена в определенную сторону от
точки А,
которую мы примем за положительную, и
отрицательной, если она отложена в
другую сторону.
Продифференцируем вектор по скаляру s. Получим вектор
,
направленный по касательной к кривой в сторону возрастания s. Модуль этого вектора
.
Следовательно,
вектор
есть единичный вектор касательной к
кривой, направленный в сторону возрастания
s.
В проекциях
(1)
и
.
Так как единичный вектор касательной лежит на самой касательной, то уравнения касательной к кривой в точке М, как известно из аналитической геометрии, напишутся так:
,
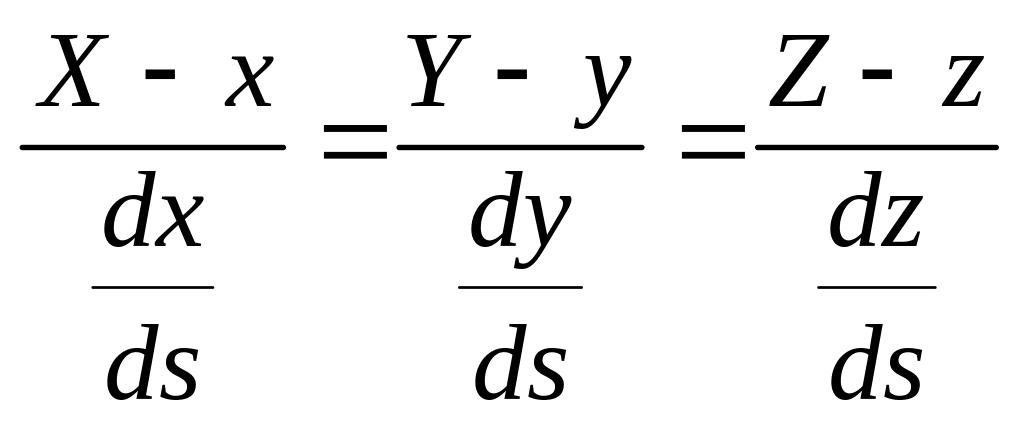(2)
где X, Y, Z − текущие координаты точки на касательной, а x, y, z − координаты точки касания, причем значения производных
берутся в точке касания.
Плоскость, перпендикулярная касательной и проходящая через точку касания, называется нормальной плоскостью.
Любая прямая, лежащая в этой плоскости и пересекающая кривую в точке касания М, будет нормалью кривой.
Уравнение нормальной плоскости можно получить, используя условия перпендикулярности прямой и плоскости. В результате получим
,
(3)
где X, Y, Z − текущие координаты точки на нормальной плоскости.
Вектор
,
как производная единичного вектора
,
перпендикулярен к последнему. Поэтому
вектор
лежит в нормальной плоскости и определяет
некоторую нормаль, называемую главной
нормалью.
Модуль
называют кривизной
кривой.
Обозначим ее через К
=
,
где R
− радиус
кривизны
:
К = = .
В проекциях
.
(4)
Тогда кривизна найдется по формуле
К
=
.
(5)
В соответствии с (4) уравнения главной нормали имеют вид
,
(6)
где X, Y, Z − текущие координаты точки на главной нормали.
Плоскость, перпендикулярная главной нормали и проходящая через точку касания, называется спрямляющей плоскостью кривой. Она определяется уравнением
.
(7)
Плоскость, проходящая через касательную и главную нормаль, называется соприкасающейся плоскостью. Эту плоскость можно определить как предельное положение плоскости, проходящей через три точки кривой, когда эти точки стремятся слиться в одну.
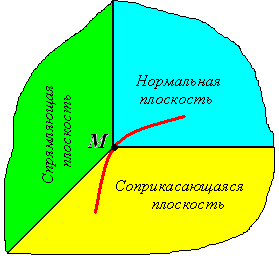
Если кривая – плоская, то касательные ко всем ее точкам находятся в одной плоскости – плоскости кривой. В этом случае соприкасающаяся плоскость совпадает с плоскостью кривой и будет одна и та же для всех ее точек. Главная нормаль кривой будет совпадать с нормалью, определенной на плоскости.
Пример. Составить уравнения касательной и нормальной плоскости к кривой
в
точке
.
□ Имеем
уравнения
касательной:
;
уравнение
нормальной плоскости:
.
Находим
,
,
.
При
имеем
,
,
,
,
,
.
Уравнения касательной:
.
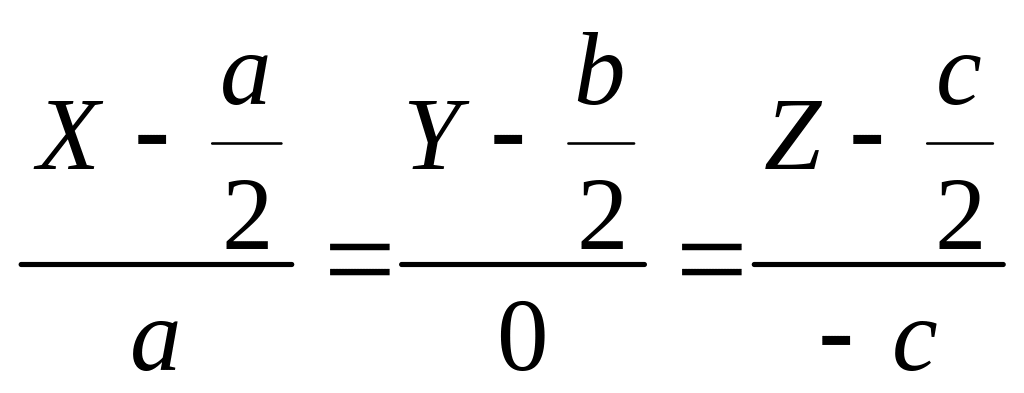Уравнение нормальной плоскости:
или
.
■
Пример.
Составить уравнения винтовой линии,
если радиус основания цилиндра R
= 4, шаг h
=
,
и найти дифференциал ее дуги.
□ Параметрические уравнения винтовой линии имеют вид
.
Согласно условию задачи получим
,
т.к.
при
.
Дифференциал дуги можно найти по формуле
=
.
Находим
,
,
.
Следовательно,
=
.
■