Висновки

Наявні два різновиди аналітичних правил для кванторних формул:

(а) з обмеженням ( T_$*, F_"*);

(б) без обмеження (T_" , F_$).

3. Cтратегії побудови аналітичних таблиць

В логіці висловлювань, будь-який порядок застосування аналітичних правил призведе до однакового результату, хоча певний порядок їх застосування може виявитись більш ефективним (економним), аніж інший. Йдеться про дві стратегії, що забезпечують економність побудови аналітичної таблиці.

(1) Закривай гілку якомога раніше.

Якщо суперечність уже наявна в гілці таблиці, подальше застосування аналітичних правил губить сенс: гілка (чи подальше розгалуження гілок) уже містить суперечність.

(2) Якщо наявна можливість уникнути розгалуження, уникай його (намагайся отримувати розгалуження якомога нижче в аналітичній таблиці).

Ігнорування цієї стратегії значно ускладнить побудову таблиці: для кожної серед отриманих гілок-розгалужень будемо вимушені записувати результати застосування аналітичних правил без розгалужень до формул, що перебувають вище пункту розгалуження.

Стратегії (1)-(2) залишаються дієвими і для логіки предикатів, але водночас з’являються додаткові стратегії.

(3) Застосовуй правила з обмеженням перед застосуванням правил без обмеження (тобто, якомога раніше застосовуй правила, які уводять нові константи).

Застосовання цієї стратегії мінімізує число констант таблиці.

Розглянемо приклад: доведемо правильність міркування „Деякі керівники держав є диктаторами. Усі диктатори мають абсолютну владу. Отже, деякі керівники держав мають абсолютну владу”. Приклад передбачає доведення загальнозначущості формули логіки предикатів, яка представляє логічну форму зазначеного міркування:

0. F [x(Rx & Dx) & x(Dx  Px)]  x(Rx & Px)

1. T x(Rx & Dx) & x(Dx  Px) F_(0)

2. F x(Rx & Px)

3. T x(Rx & Dx) T_&(1)

4. T x(Dx  Px)

5. T Ra & Da } T_(3)

6. T Ra T_&(5)

7. T Da

8. F Ra & Pa } F_(2)

9. T Da  Pa } T_(4)

10. F Ra 10’. F Pa } F_&(8)

+(6; 10)

11. F Da 11’. T Pa } T_(9)

+(7; 11) +(10’; 11’)

Якби у рядку 5. записали не результат застосування правила з обмеженням T_* до рядка 3., а, наприклад, результат застосування правила без обмеження T_ до рядка 4. (або правила без обмеження F_ до рядка 2.), тоді, незважаючи на характер застосування правил без обмеження, мусили б увести константу (наприклад, ‘а’), бо вище у таблиці не зустрічалось жодної константи, тобто:

0. F [x(Rx & Dx) & x(Dx  Px)]  x(Rx & Px)

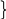1. T x(Rx & Dx) & x(Dx  Px) F_(0)

2. F x(Rx & Px)

3. T x(Rx & Dx) T_&(1)

4. T x(Dx  Px)

5. T Da  Pа } T_(4)

6. F Rа & Pа } F_(2)

Але тоді необхідність подальшого застосування правила з обмеженням до рядка 3. змусила б нас увести нову (іншу) константу, наприклад ‘b’:

7. T Rb & Db } T_(3)

Подальше застосування аналітичних правил для логічних сполучників у рядках 5., 6. і 7. не призведе до замкненості усіх гілок аналітичної таблиці. Причина відсутності замкненості – наявність різних індивідних констант:

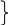8. T Rb T_&(7)

9. T Db

10. F Ra 10’. F Pa } F_&(6)

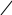
11. F Da 11’. T Pa } T_(5) 11’’. F Da 11’’’. T Pa } T_(5)

--- --- --- ---

Аби закрити гілки вимушені повертатись до рядків 2. і 4., знову застосовувати відповідні правила без обмеження, використовуючи на цей раз константу ‘b’. В результаті (разом із подальшим повторним застосуванням відповідних аналітичних правил для логічних сполучників) кожна із отриманих гілок (якою буде їх кількість?) таки виявиться замкненою, але власне процес побудови аналітичної таблиці буде неймовірно ускладненим.

Проаналізований приклад ілюструє слушність нової стратегії:

(4) Уникай уведення нових констант доти, доки це можливо (не уводь нових констант доти, доки у цьому дійсно не виникне потреба).

Два правила без обмеження (T_ i F_) не вимагають обов’язкової з’яви нових констант (вони передбачають можливість уведення будь-якої константи, незалежно від того, чи наявна вона уже в гілці аналітичної таблиці, чи ні). Отже, застосовуючи ці правила, користуйся будь-якою серед уже наявних констант. Уводь нові константи лише тоді, коли (а) цього вимагає якесь серед двох правил з обмеженням, або коли (б) жодна константа ще не наявна в гілці таблиці (гілка аналітичної таблиці не містить жодної константи).

Розглянемо приклад-ілюстрацію. Доведемо правильність міркування: „Деякі консервативні західняки є демократами. Отже, деякі демократи є консервативними”. Побудуємо аналітичну таблицю для відповідної формули, керуючись стратегією (4):

0. F x(Cx & Sx & Dx)  x(Dx & Cx)

1. T x(Cx & Sx & Dx) F_(0)

2. F x(Dx & Cx)

3. T Ca & Sa & Da } T_(1)

4. F Da & Ca } F_(2)

5. T Ca

6. T Sa T_&(3)

7. T Da

8. F Da 8’. F Ca } F_&(4)

+(7; 8) +(5; 8’)

Якщо будувати таблицю, ігноруючи вимоги стратегії (4), опинимось в ситуації, схожій до ситуації побудови таблиці, що ігнорує вимоги стратегії (3):

0. F x(Cx & Sx & Dx)  x(Dx & Cx)

1. T x(Cx & Sx & Dx) F_(0)

2. F x(Dx & Cx)

3. T Ca & Sa & Da } T_(1)

4. F Db & Cb } F_(2)

5. T Ca

6. T Sa T_&(3)

7. T Da

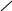
8. F Db 8’. F Cb }F_&(4)

9. F Da & Ca 9’. F Da & Ca }F_(2)

10. F Da 10’. F Ca } F_&(9) 10’’. F Da 10’’’. F Ca } F_&(9’)

+(7; 10) +(5; 10’) +(7; 10’’) +(5; 10’’’)

Приклади засвідчують: деякі аналітичні таблиці виявляться замкненими лише за умови використання належних констант під час застосування аналітичних правил для кванторів. Вище побудована таблиця не виявилась би замкненою, якби зупинились на кроці 8. Звідси, отримуємо наступну стратегії:

(5) За допомогою правил без обмеження продовжуй отримувати часткові випадки формул доти, доки не використаєш усіх уже наявних в гілці таблиці констант.

Правила без обмеження не вимагають уведення нових констант. Крім того, можна повторювати застосування таких правил, використовуючи уже наявні в гілці таблиці константи доти, доки (а) аналітична таблиця замкнеться, або (б) наявні в гілці константи виявляться вичерпаними.

Розглянемо міркування: „Джульєтта любить кожного, хто любить Ромео. Ромео любить себе. Отже, Джульєтта любить себе”. Побудуємо аналітичну таблицю для відповідної формули:

0. F [x(Lxb  Lax) & Lbb]  Laa

1. T [x(Lxb  Lax) & Lbb] F_(0)

2. F Laa

3. T x(Lxb  Lax) T_&(1)

4. T Lbb

На п’ятому кроці потрібно застосувати правило без обмеження T_ до третього рядка. Хоча замість індивідної змінної ‘х’ можемо підставляти будь-яку константу, але покладаємось на стратегії (4)-(5) побудови аналітичної таблиці і зупиняємо свій вибір, наприклад, на константі ‘а’:

5. T Lab  Laa } T_(3)

6. F Lab 6’. T Laa } T_(5)

+ (2, 6’)

Якщо на цьому етапі припинимо роботу, то отримаємо відповідь щодо неправильності міркування, оскільки одна серед гілок виявилась незамкненою. Така відповідь буде невірною! Продовжимо гілку (0.-6.), повторно застосовуючи правило без обмеження T_ до третього рядка. На цей раз замінимо індивідну змінну на іншу, але також уже наявну в даній гілці, константу ‘b’:

6. T Lbb  Lab } T_(3)

6. F Lbb 8’. T Lab } T_(7)

+ (4, 8) + (6, 8’)

На цей раз усі гілки виявились замкненими.

*****

В логіці предикатів наявна інша можливість, бо метод аналітичних таблиць не є процедурою розв’язуваності для логіки предикатів (так само, як ніщо інше не є такою процедурою; для логіки предикатів відсутня процедура розв’язуваності). Інколи застосування аналітичних правил для побудови таблиці призводить до з’яви безконечних таблиць: таблиць, що ніколи не виявляться замкненими, з огляду на неможливість завершення подальших отримань часткових випадків.

Спочатку розглянемо приклад таблиці, яка виявиться замкненою лише в результаті повторного звернення до і аналізу формули, часткові випадки якої уже були отримані в таблиці. Доведемо правильність міркування: „Хтось створив усе. Отже, усе було створеним кимось” (як варіант: „Бог створив усе. Отже, усе було створеним (кимось тим, чи кимось іншим) ”.

0. F xyCxy  yxCxy

1. T xyCxy F_(0)

2. F yxCxy

До рядків 1. і 2. треба застосовувати правила з обмеженням: T_ i F_ відповідно. Саме тому в рядках 3. і 4. з’являються нові константи ‘a’ i ‘b’:

3. T yCay } T_(1)

4. F xCxb } F_(2)

Рядки 3. і 4. вимагають застосування правил без обмеження (T_ i F_) до формул, які є частковими випадками формул із рядків 1. і 2. Рядки 5. і 6. з’являються як результат повторного звернення до формул, часткові випадки яких уже були отримані в таблиці:

5. T Cab } T_(3)

6. F Cab } F_(4)

+(5; 6)

Очевидно, що зміна послідовності кванторів, коли універсальний квантор переміщують ліворуч, зберігає істинність. Цього не можна сказати про зворотнє: переміщення екзистенційного квантору ліворуч спричинює з’яву сильнішого ствердження, яке не випливає (не слідує) із вихідного. Як приклад згодом розглянемо неправильне міркування (яке інколи приписують св.Томі Аквінському): „Усе має причину. Отже, щось є причиною усього”.

Зараз розглянемо нехарактерний випадок: інколи переміщення ліворуч екзистенційного квантору таки зберігає істинність. Це відбувається, зокрема, у випадку:

xy(Px & Gy)╞ yx(Px & Gy).

В даному прикладі зміна місць кванторів не знищує відношення логічного слідування лише тому, що змінні ‘x’ та ‘y’ не перебувають у якомусь відношенні у формулi; жодна атомарна складова формули не містить двох змінних водночас. Насправді те, що виражають і ліва, і права частини є еквівалентними до:

xPx & yGy.

Розглянемо наведений вище приклад, зважаючи на прийнятні стратегії побудови таблиці:

0. F xy(Px & Gy)  yx(Px & Gy)

1. T xy(Px & Gy) F_(0)

2. F yx(Px & Gy)

3. T y(Pa & Gy) } T_(1)

4. T Pa & Gb } T_(3)

5. T Pa T_&(4)

6. T Gb

7. F x(Px & Gb) } F_(2)

8. F Pc & Gb } F_(7)

9. F Pc 9’. F Gb } F_&(8)

+(6; 9’)

На цьому етапі можна було б помилково зупинитись і заявити, що позаяк одна з гілок (1.-9.) є відкритою, досліджуване відношення логічного слідування насправді відсутнє. Але рядок 1. залишає можливість повторного застосування правила без обмеження T_ для отримання не лише часткового випадку фомули із константою ‘а’ (як це дійсно відбувалось), але і з константами ‘b’ або ‘с’. Схожим чином, рядок 2. залишає можливість повторного застосування правила без обмеження F_ для отримання не лише часткового випадку формули із константою ‘b’ (як це дійсно відбувалось), але і з константами ‘a’ або ‘с’. Здається доречним використати константу ‘с’ в новому (повторному) отриманні часткового випадку формули із рядка 1. з метою перетворення гілки (1.-9.) на замкнену:

10. T y(Pс & Gy) } T_(1)

11. T Pc & Gd } T_(10)

12. T Pc T_&(11)

13. T Gd

+(9; 13)

Розглянемо іще один приклад, коли таблиця залишається незамкненою, незважаючи на те, що усі підходящі можливості для отримання часткових випадків формул вичерпані. Розглянемо низку відношень.

Відношення R є рефлексивним, якщо і тільки якщо для кожного х справедливо: R наявне між х і х (таке відношення, в якому перебуває кожний індивід із самим собою). Тобто, xRxx ( ~x~Rxx).

Приклади рефлексивних відношень: „бути однакового віку (ваги,зросту)”, =, , .

Відношення R є симетричним, якщо і тільки якщо для будь-яких х і у справедливо: якщо R наявне між х і у, то R наявне також між у і х. Тобто, xy(Rxy  Ryx) (  ~xy(Rxy & Ryx)).

Приклади: „бути братом або сестрою”, „бути того ж самого віку”, =.

Відношення R є транзитивним, якщо і тільки якщо для будь-яких х, у і z справедливо: якщо R наявне між х і у, а також між у і z, то R наявне також між х і z. Тобто,

xyz((Rxy & Ryz)  Rxz) ( ~xyz((Rxy & Ryz) & ~Rxz)).

Приклади: „бути того ж самого віку”, „бути залежним від”, =, , , , .

Чи будуть усі відношення, що є симетричними і транзитивними рефлексивними?

Досліджуючи, чи дійсно:

xy(Rxy  Ryx) & xyz((Rxy & Ryz)  Rxz) ╞ xRxx

побудуємо відповідну аналітичну таблицю, керуючись зазначеними вище стратегіями:

0. F [xy(Rxy  Ryx) & xyz((Rxy & Ryz)  Rxz)]  xRxx

1. T xy(Rxy  Ryx) & xyz((Rxy & Ryz)  Rxz) F_(0)

2. F xRxx

3. T xy(Rxy  Ryx) T_&(1)

4. T xyz((Rxy & Ryz)  Rxz)

5. F Raa } F_(2)

6. T y(Ray  Rya) } T_(3)

7. T Raa  Raa } T_(6)

8. T yz((Ray & Ryz)  Raz) } T_(4)

9. T z((Raa & Raz)  Raz) } T_(8)

10. T (Raa & Raa)  Raa } T_(9)

11. F Raa 11’. T Raa } T_(7)

+(5; 11’)

12. F Raa & Raa 12’. T Raa } T_(10)

+(5; 12’)

13. F Raa 13’. F Raa } F_&(12)

--- ---

Ми вичерпали усі підходящі для побудови даної таблиці часткові випадки формул. Стратегія побудови говорить: отримання (за відсутності потреби) часткових випадків формул із відсутніми раніше у гілці таблиці константами позбавлене сенсу. Тому, отримання, наприклад, константи ‘b’ нічим не зарадить. Завершення отримання усіх можливих часткових випадків формул із константою ‘а’ засвідчує завершення процесу побудови. Позаяк наявні відкриті гілки таблиці, відношення логічного слідування відсутнє.

Розглянутий приклад засвідчує: отримання часткових випадків формул, що складаються із низки лише універсальних кванторів, або із низки лише екзистенційних формул, за умови застосування правил без обмеження(T_ i F_) є даремною справою. В таких випадках можемо підставляти будь-яку константу замість будь-якої змінної, а також „скидати” відразу декілька кванторів і здійснювати декілька підстановок водночас. Наприклад, за потреби отримання в таблиці часткових випадків формули xy(Rxy  Ryx), можемо відразу переходити до формули Raa  Raa, або Rab  Rba,

Rba  Rab, Rbb  Rbb і т.д.

Схожим чином, зручно водночас опрацьовувати формули, що містять низку лише універсальних кванторів, або низку лише екзистенційних кванторів, за умови застосування до них правил з обмеженням (F_* i T_*). Однак, кожне окреме застосування таких правил вимагає з’яву нової константи. За наявності десь вище в гілці аналітичної таблиці, наприклад, лише константи ‘а’, можемо відразу перейти від формули xyz(Sxy & Sxz) до формули Sbc & Sbd.

Зважаючи на техніку спрощеної побудови таблиці, отримаємо для попереднього прикладу:

0. F [xy(Rxy  Ryx) & xyz((Rxy & Ryz)  Rxz)]  xRxx

1 . T xy(Rxy  Ryx) & xyz((Rxy & Ryz)  Rxz) F_(0)

2. F xRxx

3 . T xy(Rxy  Ryx) T&(1)

4. T xyz((Rxy & Ryz)  Rxz)

5. F Raa } F_(2)

6. T Raa  Raa } T_,(3)

7. T (Raa & Raa)  Raa } T_,,(4)

8. F Raa 8’. T Raa } T_(6)

+(5; 11’)

9. F Raa & Raa 9’. T Raa } T_(7)

+(5; 12’)

10. F Raa 10’. F Raa } F_&(9)

--- ---

Деякі таблиці ніколи не закриються, хоча запаси констант не будуть вичерпаними. Такі безконечні таблиці (таблиці, побудова яких ніколи не закінчиться) є джерелом нерозв’язуваності кванторної логіки. Відсутній спосіб встановлення, коли побудова деякої таблиці закінчиться. У багатьох простих випадках, однак, легко сказати, що таблиця ніколи не закриється; вона заманює нас до петлі, яка постійно спонукатиме до уведення нових констант.

Повернемось до розгляду міркування: „Усе має причину. Отже, щось є причиною усього”. Спробуємо дослідити це міркування, будуючи відповідну аналітичну таблицю:

0. F xyCyx  yxCyx

1. T xyCyx F_(0)

2. F yxCyx

Подальша побудова таблиці призводить до петлі, де уводяться усе нові і нові константи, отримуються нові часткові випадки формул, затим знову уводяться нові константи і т.д. до безконечності:

3. T yCya } T_(1)

4. T Cba } T_(3)

5. F xCbx } F_(2)

6. F Cbc } F_(5)

7. T yCyc } T_(1)

8. T Cdc } T_(7)

9. F xCdx } F_(2)

10. F Cde } F_(9)

.

.

.

Очевидно, що побудова таблиці ніколи не закінчиться. Так саме очевидно, що ніколи не отримаємо в такій побудові суперечності.

До теми 4

Прості категоричні висловлювання

A(SP) Усі S є Р загально - стверджувальне

E(SP) Жодне S не є Р загально - заперечне

I(SP) Деякі S є Р частково - стверджувальне

O(SP) Деякі S не є З частково - заперечне

Три групи законів силогістики

1. Закони логічного квадрату – регулюють відношення між ПКВ на підставі

їх значень істинності.

2. Закони безпосередніх умовиводів – регулюють припустимі трансформації

ПКВ.

3. Закони простого категоричного силогізму (ПКС) – стосуються міркувань,

які складаються із 3 (серед зазначених 4 видів) ПКВ.

Логічний квадрат

A(SP) E(SP)

I(SP) O(SP)

1) Закон суперечності (контрадикторності): два висловлювання, що суперечать одне одному

([A -O] i [E – I]) не можуть бути одночасно істинними і не можуть бути одночасно хибними.

2) Закон протилежності (контрарності): два висловлювання, що перебувають у відношенні

протилежності ([A – E]) не можуть бути одночасно істинними.

3) Закон підпротилежності (субконтрарності): два висловлювання, що перебувають у

відношенні підпротилежності ([І – О]) не можуть бути одночасно хибними.

4) Закон підпорядкування: а) із істинності загального висловлювання (А чи Е) логічно слідує

істинність відповідного часткового висловлювання (І чи О), але не навпаки; б) із хибності

часткового висловлювання (І чи О) логічно слідує хибність відповідного загального

висловлювання (А чи Е), але не навпаки.