Властивості скалярного добутку векторів:

1. 

2. 

3. 

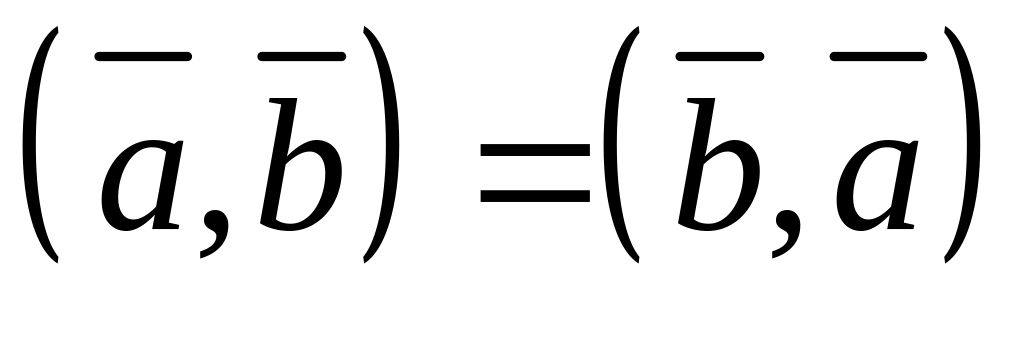
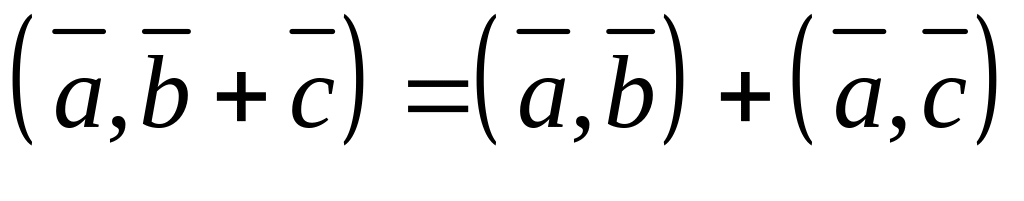
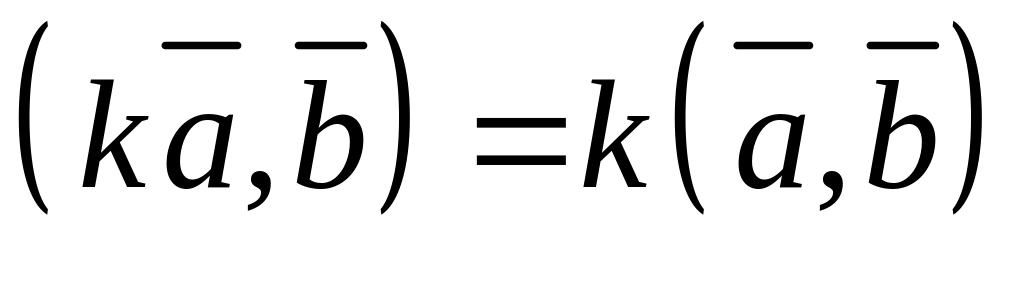
4. , причому тоді і тільки тоді, коли

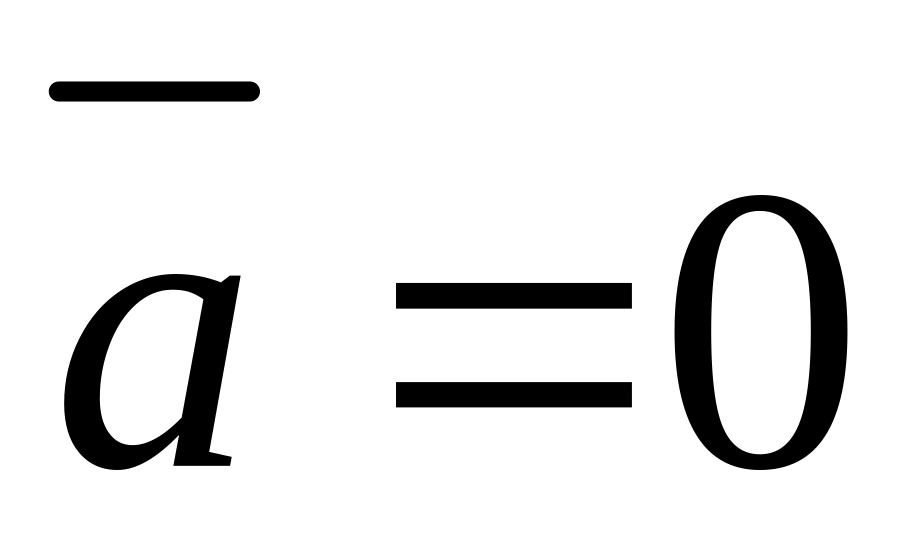
2.1.4. Координати вектора. Довжина вектора. Кут між векторами

Координати вектора дорівнюють різниці відповідних координат кінця та початку вектора. Якщо і - відповідно початок та кінець вектора, то

Довжиною {нормою) вектора (позначають ) називають невід'ємне значення квадратного кореня з суми

квадратів координат вектора, тобто

Наприклад, якщо , то .

Кутом між ненульовими векторами і називається число , яке визначається рівністю

Приклад 2.1. Знайти кут між векторами

Розв'язання

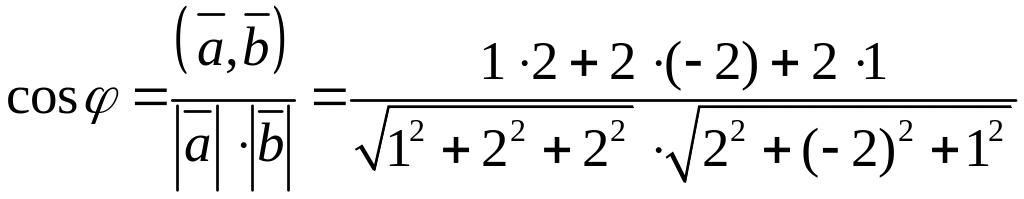
Відповідь: .

2.1.5. Лінійна залежність і незалежність векторів. Розкладання вектора за базисом

Нехай вектори з -вимірного векторного про­стору, а - деякі дійсні числа.

Вектор називається лінійною ком­бінацією векторів .

Вектори називаються лінійно залежними, як­що існують такі дійсні числа , одночасно не рівні ну­лю, такі що

Якщо рівність справджуються тіль­ки тоді, коли , то вектори назива­ються лінійно незалежними.

Для перевірки векторів на лінійну незалежність по­трібно скласти із координат векторів визначник, який не пови­нен дорівнювати нулю:

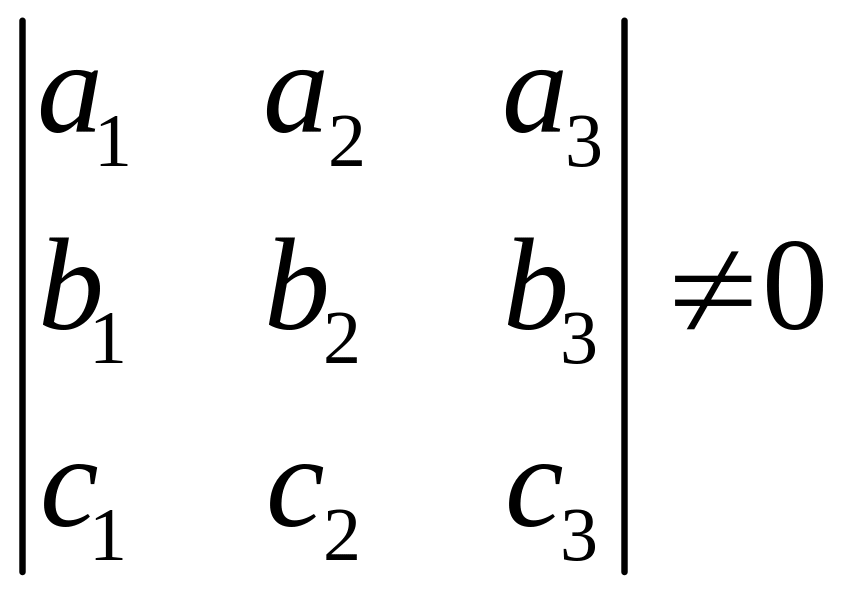
Теорема 1. Вектори лінійно залежні тоді і тіль­ки тоді, коли хоча б один з них є лінійною комбінацією інших.

Вимірність простору - це максимальна кількість ліній­но незалежних векторів, що містяться у ньому. Будь-яку сукуп­ність лінійно незалежних векторів -вимірного лінійного прос­тору називають його базисом.

Теорема 2. Будь-який вектор з єдиним способом може бути зображений у вигляді лінійної комбінації векторів базису.

Якщо - базис лінійного простору vя, то

- розклад вектора за базисом ,

- координати вектора у цьому базисі.

Алгоритм розкладу вектора за базисом

1. Записати рівність у формі матри­чного рівняння, де вектори записати у вигляді мат риць-стовпців.

2. Від матричного рівняння перейти до системи лінійних алгебраїчних рівнянь та розв'язати одержану систему.

3. Записати розклад вектора за базисом . Для цього в рівність замість підстави­ти розв'язки системи.

Приклад 2.2. Написати розклад вектора у бази­сі .

Розв'язання

Використаємо формулу розкладу вектора за базисом

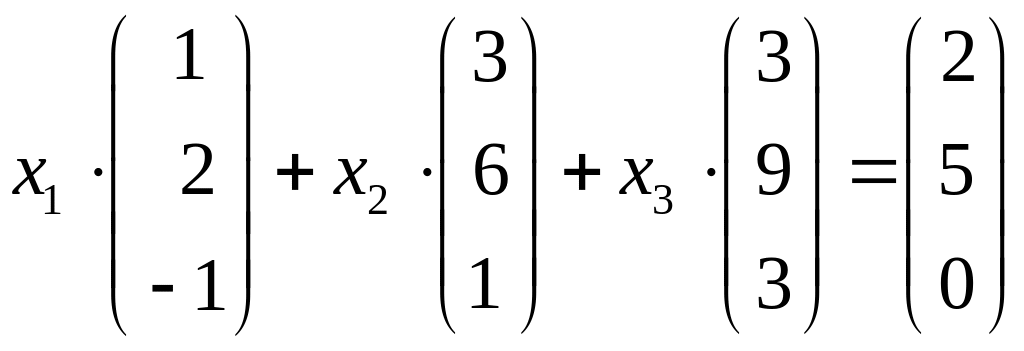
Розв'язком цієї системи є .

Так, - розклад вектора в базисі .

Відповідь.

2.2. Лінії на площині

2.2.1. Прямокутна декартова система координат на площині та у просторі

Числовою віссю називають пряму, на якій визначено на­прям, початок відліку та одиничний відрізок (рис. 1).

Координатою точки на осі називають відстань від цієї точки до початку відліку, що береться зі знаком "+", як­що точка лежить на додатній півосі, і зі знаком "-", якщо вона лежить на від'ємній півосі. Позначають .

Дві взаємно перпендикулярні числові осі з спільним по­чатком відліку називають прямокутною декартовою систе­мою координат (або просто прямокутною системою коорди­нат) на площині (рис. 2).

Горизонтальну вісь називають віссю абсцис (вісь ), а вертикальну - віссю ор­динат (вісь ).

Точку перетину осей координат нази­ вають початком координат (точка О). Одиниці масштабу на обох осях, як прави­ло, вибирають однаковими.

Довільній точці площини можна поставити у відповід­ність два числа і - координати її проекцій на осі абсцис і ор­динат відповідно.

Числа і однозначно визначають положення точки М на площині і називаються координатами точки: - абсцисою, а - ординатою точки (записують ). Початок коорди­нат - точка .

Осі координат розбивають площину на чотири частини, які називають координатними чвертями (квадрантами).

Три взаємно перпендикулярні числові осі зі спільним по­чатком відліку називають прямокутною системою координат у просторі (рис. 3).

Вісь називають віссю абсцис, - віссю ординат, - віссю аплі­кат

Числа та , координати проекції точки на осі абсцис, ординат та аплікат однозначно визначають положення точки у просторі і називаються координа­тами точки : - абсцисою, - орди­натою, а - аплікатою точки ( записують М (х; у; г)).

Площини та , називаються координатни­ми площинами. Вони ділять простір на 8 частин, які називають­ся октантами.

Введення прямокутної системи координат на площині (у просторі) дозволяє встановити однозначну відповідність між множиною всіх точок площини (простору) та множиною впоря­дкованих пар (трійок) чисел, що дає можливість при розв'язанні геометричних задач застосовувати алгебраїчні методи.