Алгоритм методу Гаусса

1. Скласти розширену матрицю системи.

2. Зробити так, щоб коефіцієнт 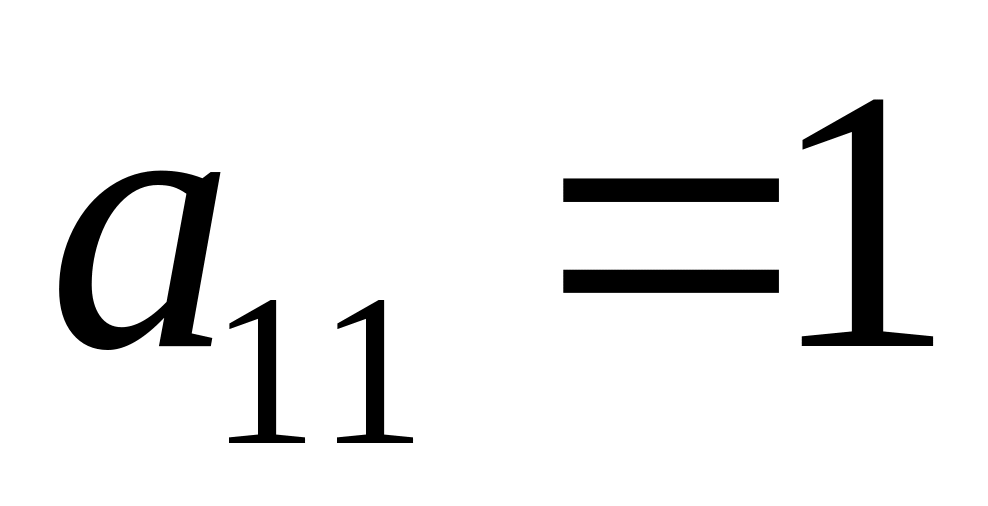. Для цього можна поміняти рядки місцями, або поділити перший рядок на аи.

3. У першому стовпці під коефіцієнтом 1 зробити всі ну­лі. Для цього помножити перший рядок послідовно на 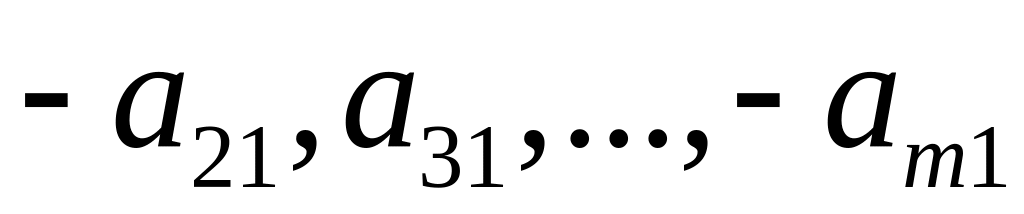і додати відповідно до другого, третього, ..., -го рядків.

4. Зробити так, щоб коефіцієнта , а під ним були нулі.

5. Описані дії повторити для всіх діагональних елементів (з однаковими індексами).

6. Знайти ранги основної і розширеної матриці системи.

7. За останньою матрицею скласти систему лінійних рів­нянь та дослідити її:

1. якщо ранги основної і розширеної матриці не рівні, то система розв'язків не має;

2. якщо ранги основної і розширеної матриці рівні та ранг системи дорівнює кількості невідомих, то система має єди­ний розв'язок.

Його шукають так: з одержаної системи послідовно, по­чинаючи з останньої за номером невідомої, рухаючись знизу вгору, знаходять усі інші невідомі.

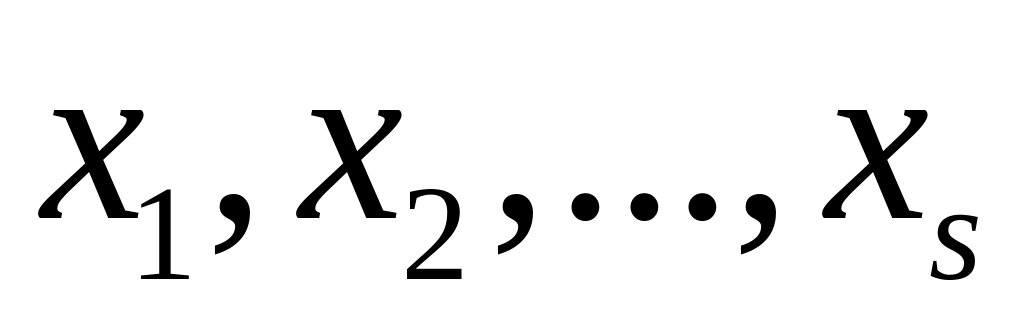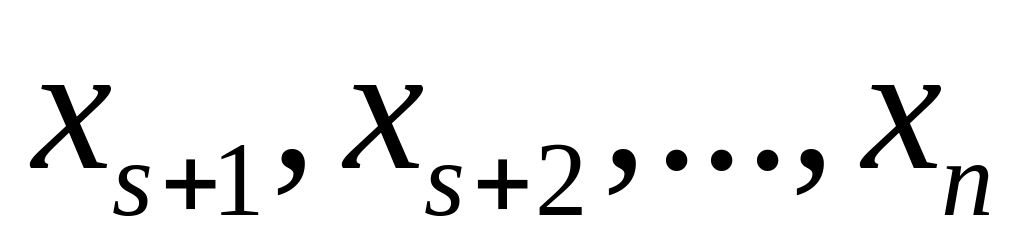3. якщо ранги співпадають, але ранг системи і' менший, ніж кількість невідомих , то ця система невизначена. Розв'язки її шукають так: перші невідомих , які називаються ба­зисними визначають через інші невідомі ,які нази­ваються вільними.

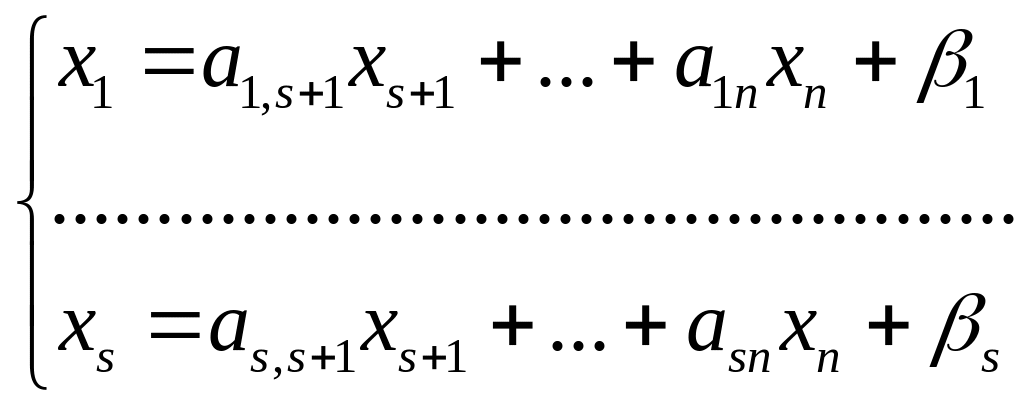- загальний розв 'язок системи.

Якщо замість підставити конкретні числові значення, то отримаємо частинний розв'язок системи. Зокре­ма, якщо , то одержимо розв'язок , який називають базисним.

Приклад 1.13. Розв'язати методом Гаусса систему ліній­них рівнянь

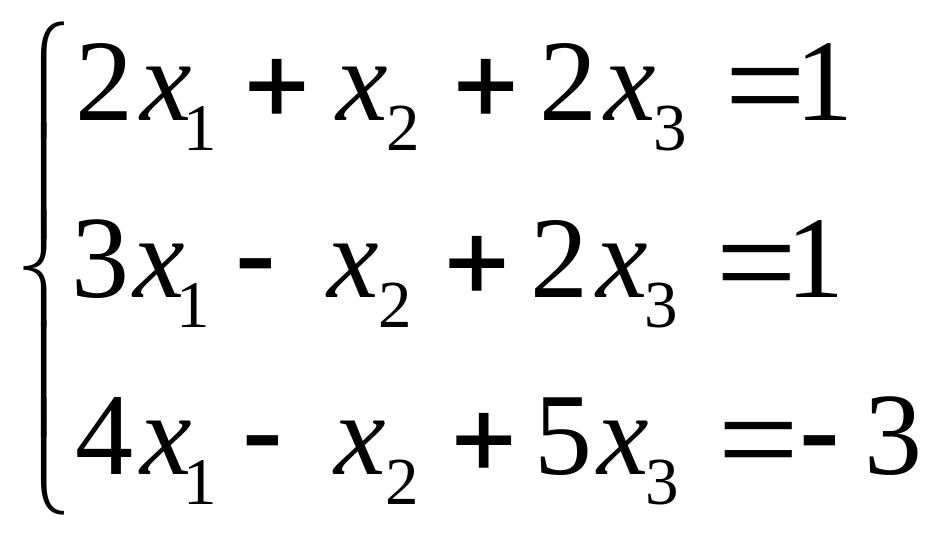
Розв'язання

1. Виконуємо перетворення над розширеною матрицею системи:

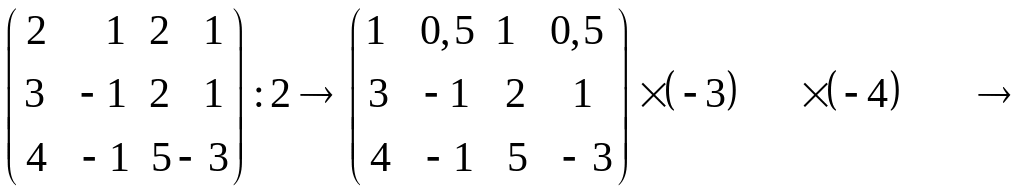
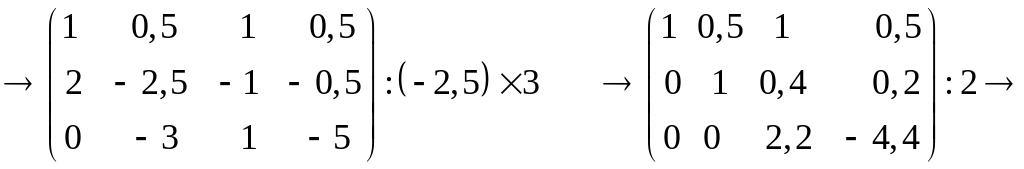
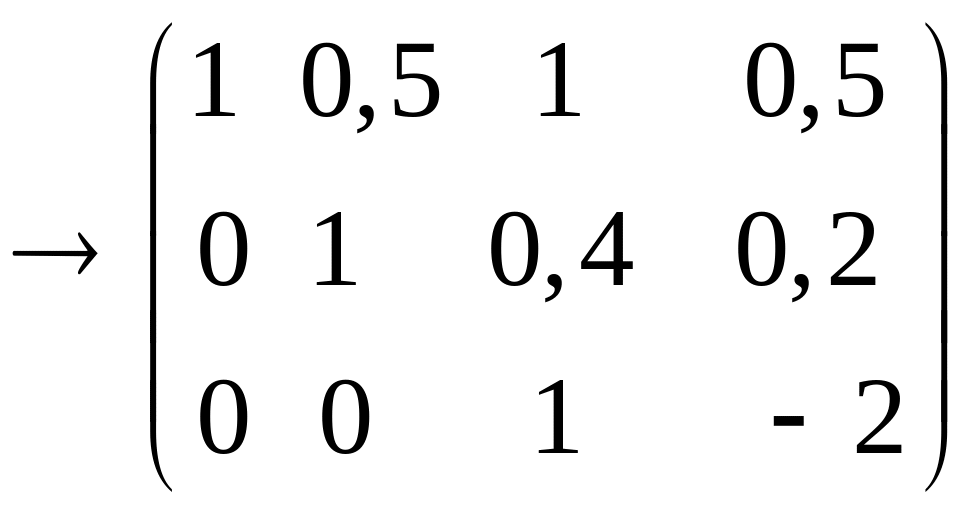
Оскільки ранги основної і розширеної матриці співпада­ють ( ) і ранг системи дорівнює кількості невідомих, то сис­тема має один розв'язок.

2. За останньою матрицею складаємо систему рівнянь.

(2; 1; -2 ) - розв'язок системи.

Відповідь. (2; 1;-2).

Приклад 1.14. Розв'язати методом Гаусса систему ліній­них рівнянь

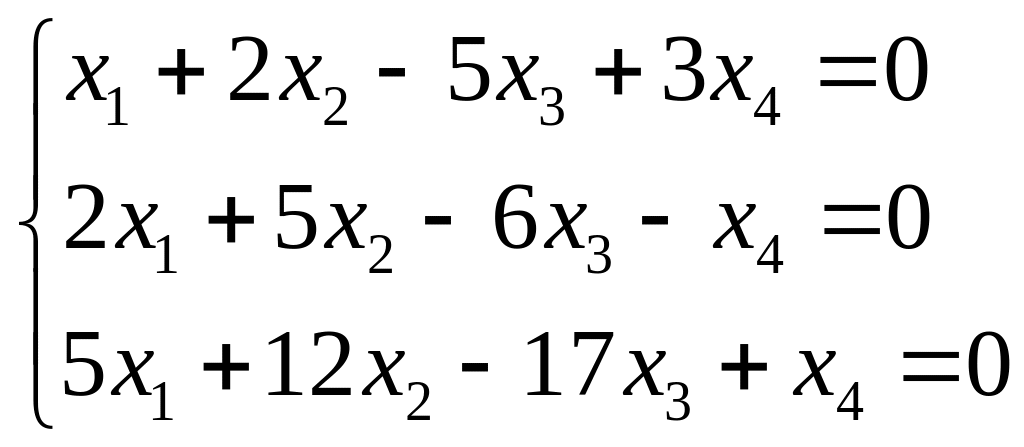
Розв'язання

1. Виконуємо перетворення над розширеною матрицею системи:

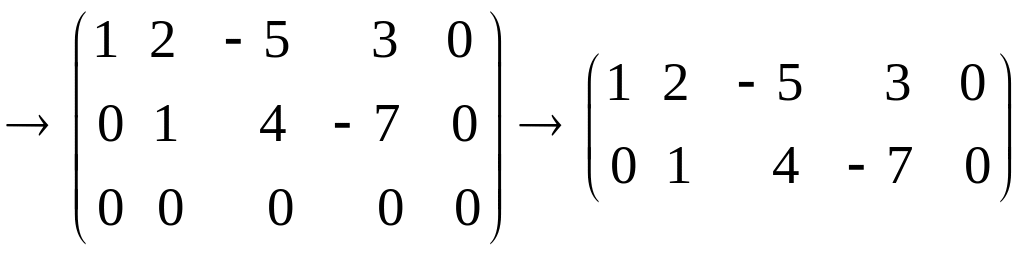
Ранги матриць співпадають ( ), значить система сумі­сна.

Оскільки ранг менше числа невідомих , то система невизначена.

2. За останньою матрицею складаємо систему рівнянь.

,

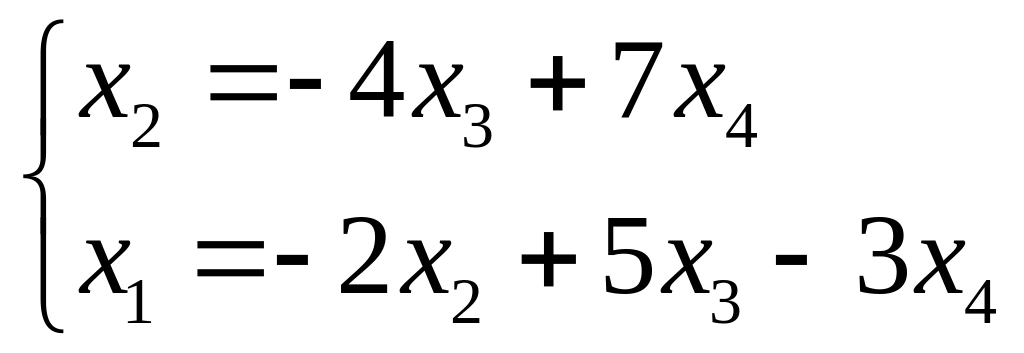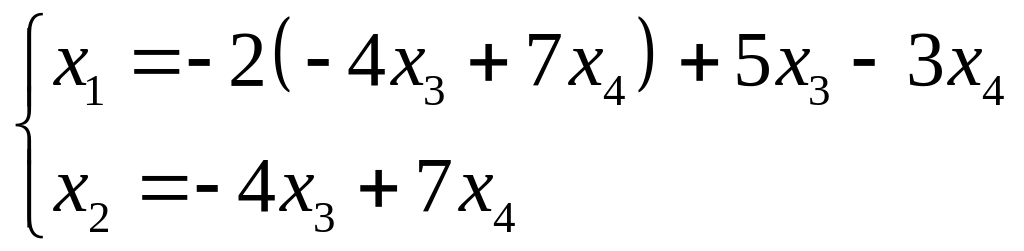
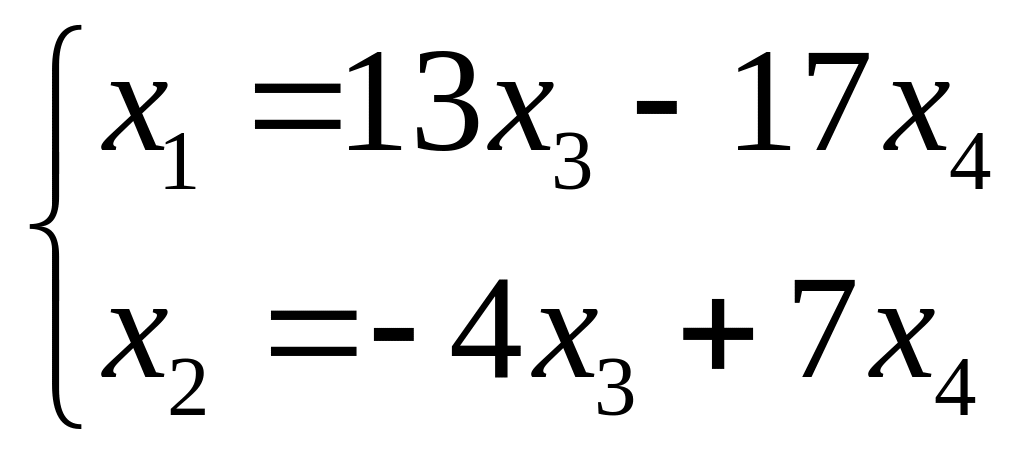- загальний розв'язок системи.

Відповідь. .

1.2.5. Метод Жордана-Гаусса розв'язування

систем лінійних рівнянь

Метод Жордана-Гаусса (метод повного виключення невідомих) є модифікацією методу Гаусса. Відрізняється від ме­тоду Гаусса тим, що невідомі виключаються не тільки з розмі­щених нижче, а й з усіх рівнянь.

Приклад 1.15. Методом Жордана-Гаусса розв'язати сис­тему рівнянь

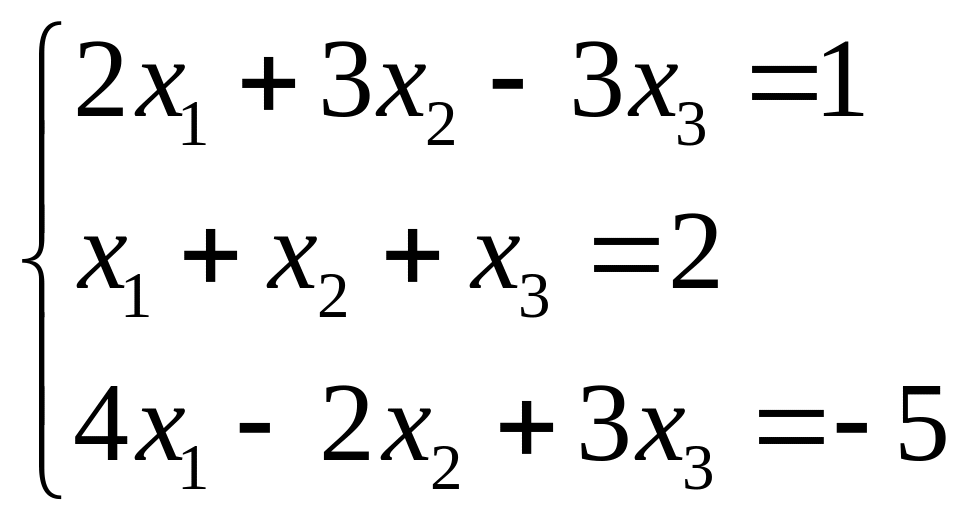
Разв'язання

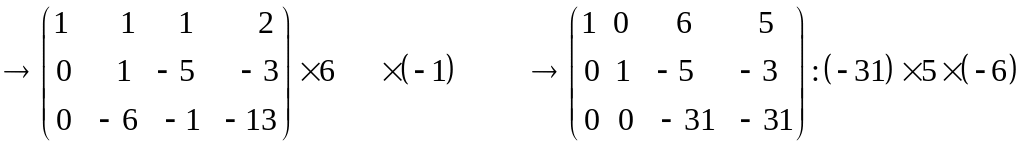
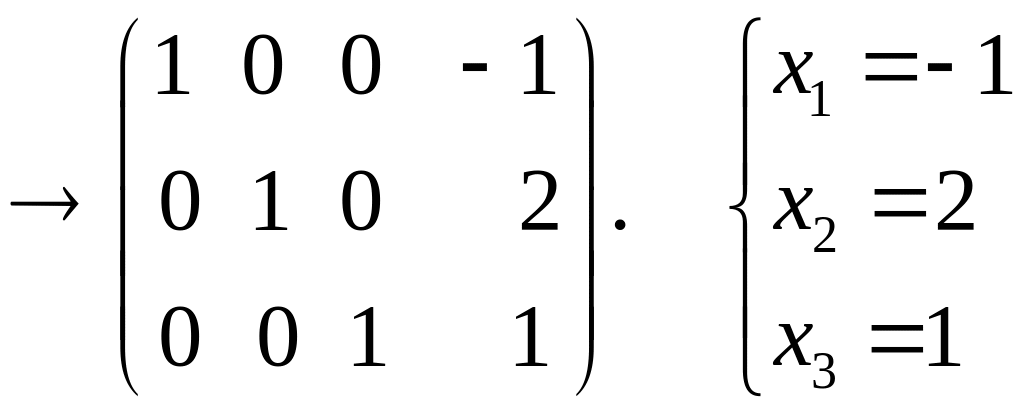
Відповідь. (-1; 2; 1).

1,2.6. Економічні приклади і задачі

1.2.6.1. Застосування матриць в економічних розрахунках

Приклад 1.16. Дані про сукупний продаж деякого това­ру фірми "Аріон" за перше та друге півріччя року задано матри­цями:

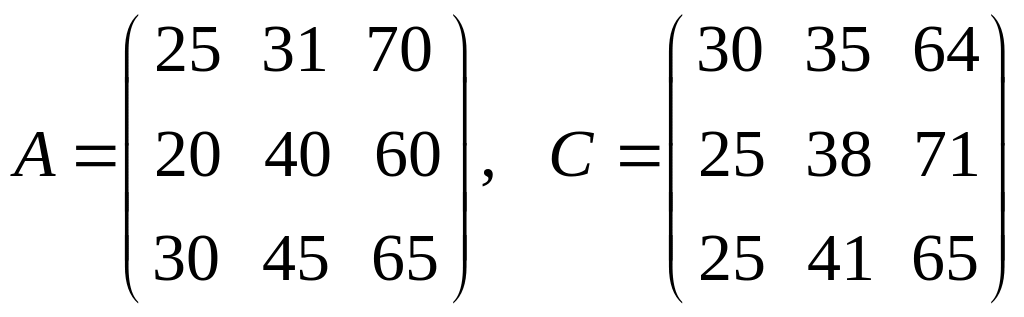
Знайти дані про сукупний продаж товару за рік.

Розв'язання

Сукупний продаж товару за рік дорівнює сумі матриць і .

Відповідь.

Приклад 1.17. У магазин надійшло три види продукції у кількостях 25, 40, 30. Вартість одиниці продукції кожного виду дорівнює відповідно 2 грн, 5 грн, 6 грн. Знайти вартість усього отриманого товару.

Розв'язання

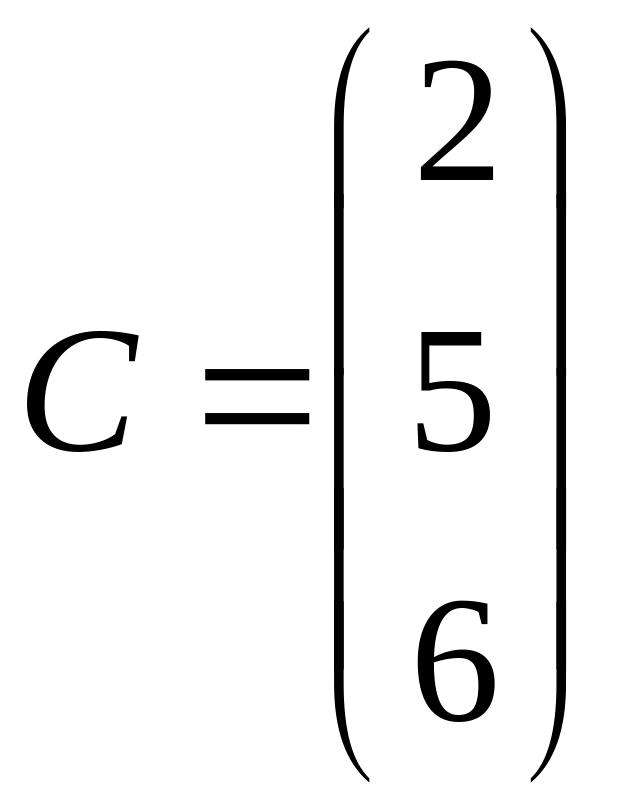Кількість товару, що отримав магазин, позначимо через матрицю , а вартість одиниці кожного виду продукції як матрицю . Тоді вартість усього товару дорівнює

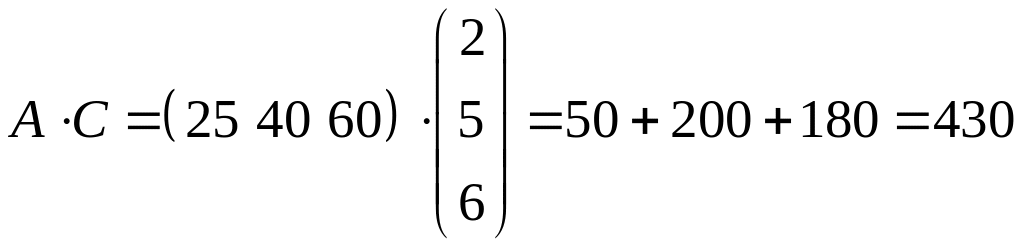(грн).

Відповідь. 430 грн.