3.2.5. Поняття границі функції. Односторонні границі

Число називається границею функції/ в точці (при ), якщо для будь-якого знайдеться такс число , що при всіх , які задовольняють нерівність виконуєть­ся нерівність , тобто .

Функція називається нескінченно малою в точці , якщо . Функція називається нескінченно великою в точці , якщо

Зауваження,

Односторонні границі

Якщо шукається при умові, що д: приймає значення менші за , то ця границя, якщо вона існує, називається лівосторонньою і позначається ;

Якщо приймає значення більші за , то границя назива­ється правосторонньою і позначається

Приклад З.5 Знайти правосторонню та лівосторонню границі функції в точці .

Розв'язання

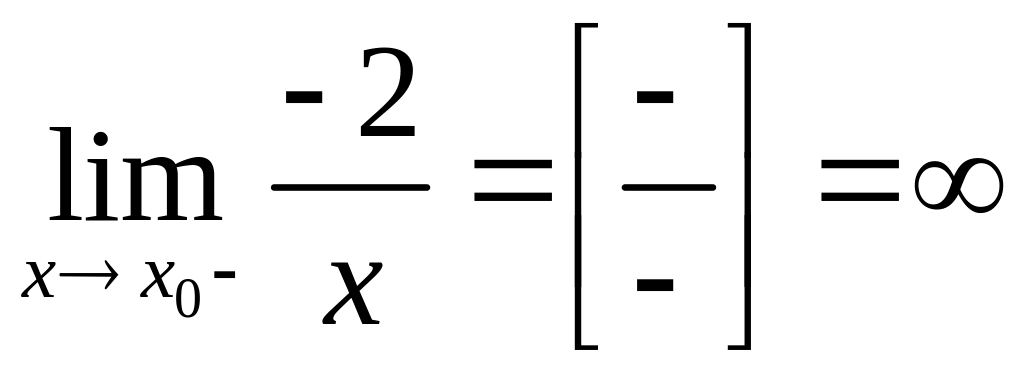
3.2.6. Основні теореми про іраниці. Чудові границі

1. Границя суми (різниці) двох функцій дорівнює сумі (різниці) границь цих функцій, якщо границі доданків існують, тобто

2. Границя добутку двох функцій дорівнює добутку границь цих функцій, якщо границі співмножників існують, тобто

3. Границя частки двох функцій дорівнює частці гра­ниць цих функцій, якщо границі чисельника і знаменника існу­ють. а границя знаменника не дорівнює нулю, тобто

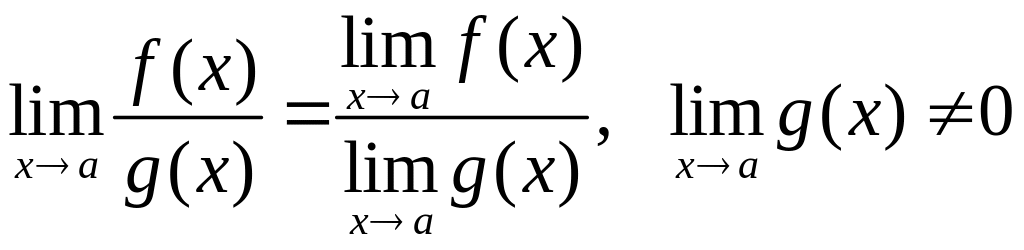
4. Стаїий множник можна винести за знак границі тобто

5. Границя цілого додатного степеня функції дорівнює тому ж степеню границі функції, тобто

Перша важлива границя:

Наслідки:

1. 

2. 

3. 

4. 

Друга важлива границя: 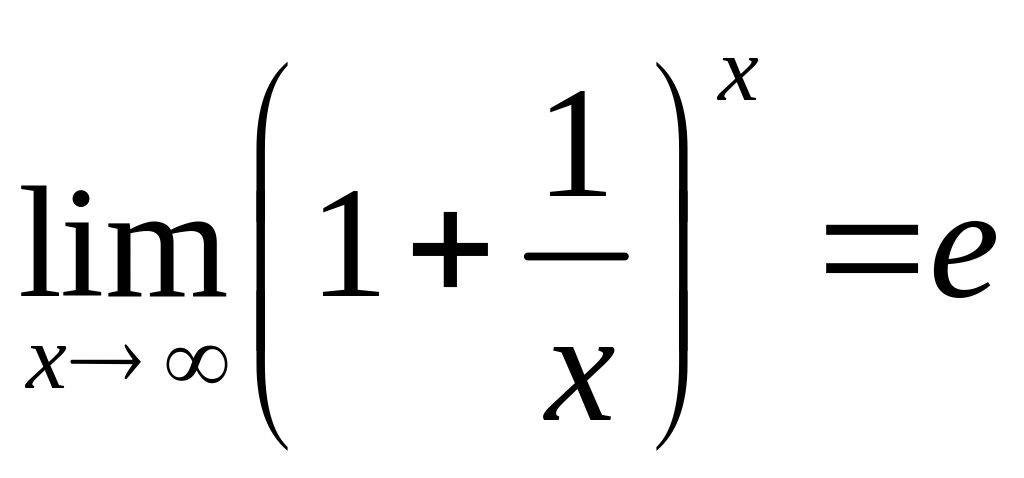, де

Наслідки:

1. 

2. 

3.2.7. Прийоми обчислення границь функції

1. Пробуємо підставити значення у функцію .

Приклад 3.6.

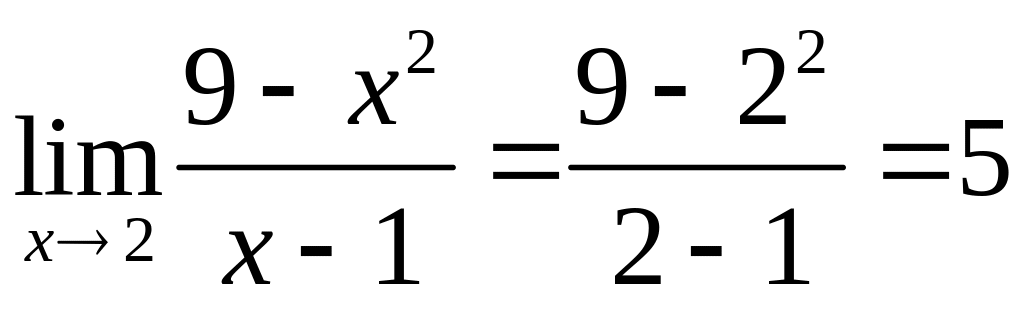
2. Розкриття невизначеності : в чисельнику і зна­меннику винести за дужки найвищий степінь невідомого.

Приклад 3.7.

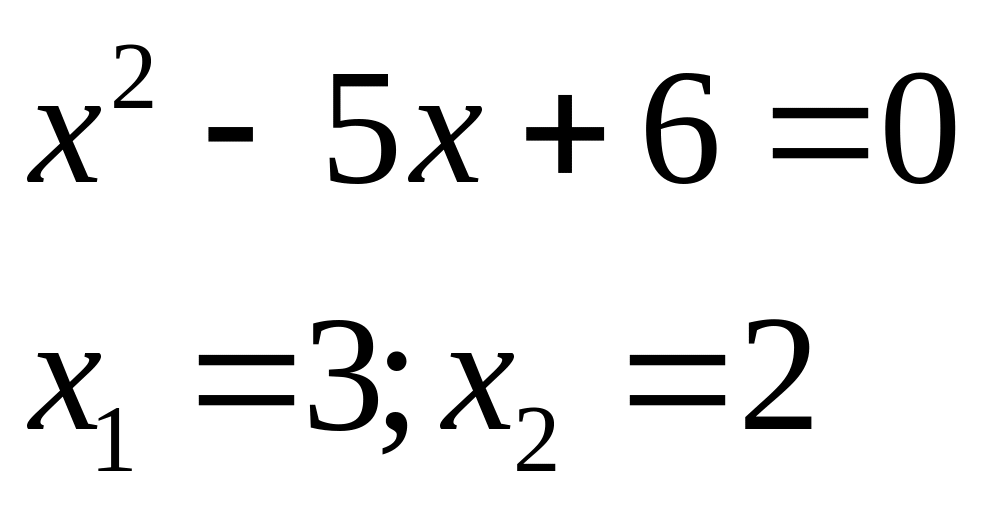
3. Розкриття невизначеності :

а) розкласти чисельник і знаменник на множники:

Приклад 3.8

б) якщо до чисельника або знаменника входять квадратні чи кубічні корені, то потрібно домножити чисельник і знаменник на відповідні вирази, щоб позбутися коренів:

Приклад 3.9.

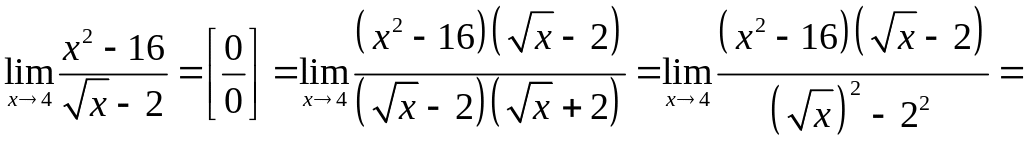
в) якщо під знаком границі стоять тригонометричні або обернені тригонометричні функції, то такі границі зводяться до першої визначної границі або її варіацій (наслідків).

Приклад 3.10.

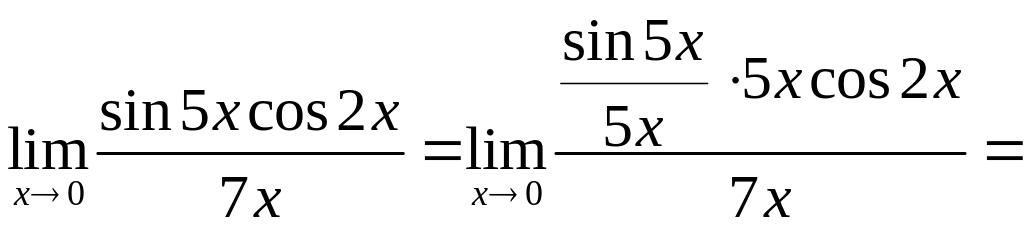
4. Розкриття невизначеності звести до другої визнач­ної границі:

Приклад 3.11. .

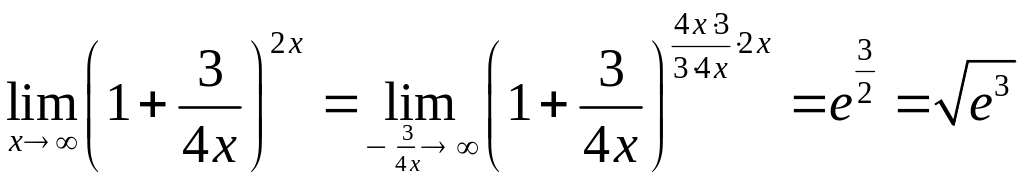3.2.8. Неперервність функції. Основні поняття

Функція називається неперервною в точці , якщо границя функції в точці дорівнює значенню функції в цій точці:

Приклад 3.12. Довести неперервність функції в точці .

Розв'язання

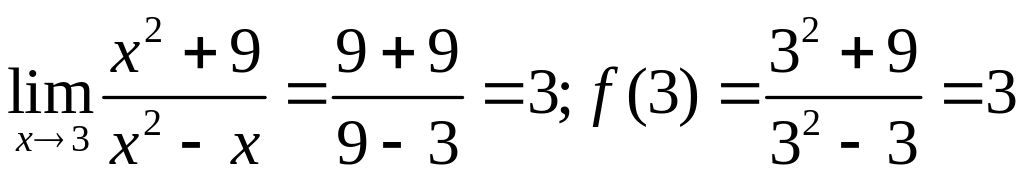
Оскільки , то задана функція неперервна в точці , що і треба було довести.

Функція називається неперервною в точці , якщо

• визначена в точці ,

• границя зліва в точці дорівнює іраниці справа в цій точці і дорівнює значенню в ній функції:

Функція неперервна на проміжку, якщо вона неперервна в кожній точці цього проміжку.

Функція неперервна на відрізку , якщо вона неперервна на проміжку і неперервна в точці справа і в точці зліва.