Лекция № 10.

Тема: ТЕОРЕМА ПОЛНОТЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ

Основные вопросы, рассматриваемые на лекции:

1. Лемма 1: 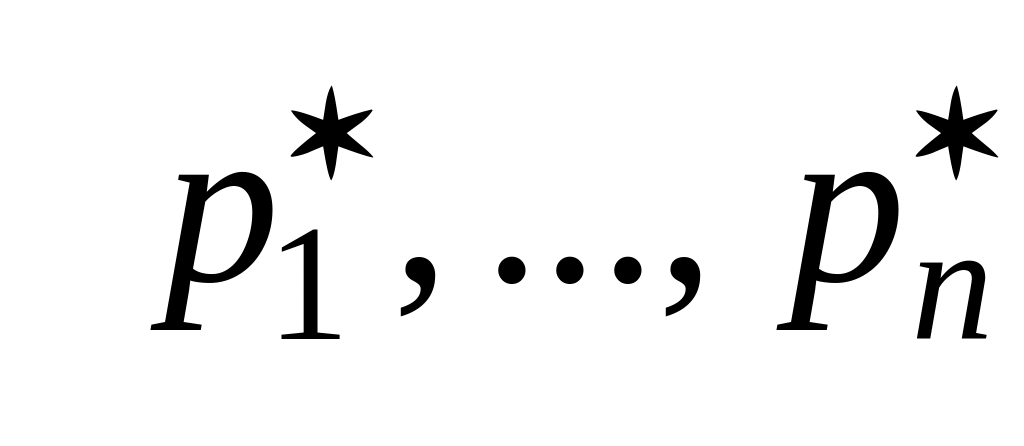^_S1A^

2. Доказатьельство леммы 1 индукцией по формулам

3. Теорема полноты исчисления высказываний

Краткое содержание лекционного материала

Предположим, что в состав формулы A входят только следующие пропозициональные переменные p₁,…,p_n. Если дано некоторое распределение истинностных значений переменных p₁,…,p_n, то примем следующее обозначение: , где i1,…,n, и

Лемма 1. Имеет место следующее следствие системы S₁:

^_S1A^. (1)

Доказательство индукцией по формулам.

Если Ap_i, i1,…,n, то A^p_i^, и (1) верно по определению следствия.

Пусть AB. Тогда по индуктивному предположению

^_S1B^. (2)

Возможны два случая: BИ и BЛ.

Если BИ, AЛ, то A^AB, BИ, B^B, (1) следует из (2) и (P₄).

Если A^AB, BЛ, B^B, то (1) есть (2).

Пусть ABC. Тогда по индуктивному предположению верно (2) и

^_S1C^. (3)

Возможны три случая: BИ и CЛ; BЛ; CИ.

Если BИ и CЛ, то AЛ, A^A(BC), B^B, C^C, (1) следует из (2) и (P₈).

Если BЛ, то AИ, A^ABC, B^B, (1) следует из (2) и (P₅).

Если CИ, то AИ, A^ABC, C^C, (1) следует из (3) и (P₁). 

Теорема полноты. Если A – тавтология, то ^_S1A.

Доказательство. Так как A – тавтология, то A^A.

В силу леммы 2, ^_S1A, ^_S1A.

В силу теоремы 4, ^_S1 p_nA, ^_S1 p_nA.

Отсюда и из (P₆) следует, что ^_S1A, и, аналогично получается, что ^_S1A, …, ^_S1A, ^_S1A, ^_S1A. 

Лекция №11.

Тема: ПРЕДИКАТЫ И ОПЕРАЦИИ НАД НИМИ

Основные вопросы, рассматриваемые на лекции:

1. Определение n-местного предиката

2. Область определения и множество истинности предиката

3. Операции над предикатами Краткое содержание лекционного материала

n-местным предикатом AP(x₁,…,x_n) называется математическое предложение, содержащее n свободных переменных x₁,…,x_n. Говорят, что вхождение переменной в предложение или формулу свободно, если переменную можно заменять ее допустимым значением. Синонимы термина предикат: свойство, условие, отношение.

n-местный предикат AP(x₁,…,x_n) при замене всех свободных вхождений переменной x_n ее допустимым значением d_n обращается в (n1)-местный предикат BP(x₁,…,x_n1,d_n)P(x₁,…,x_n1) (n1). Одноместный предикат AP(x) при замене всех свободных вхождений переменной x ее допустимым значением d обращается в высказывание AP(d).

Пусть D₁,…,D_n – множества допустимых значений соответственно переменных x₁,…,x_n. Множество (декартово произведение)

D_PD₁…D_n(d₁,…,d_n)d₁D₁,…,d_nD_n

всех упорядоченных n-ок элементов множеств D₁,…,D_n называется областью определения n-местного предиката P(x₁,…,x_n).

Множеством истинности n-местного предиката P(x₁,…,x_n) называется множество M_P(d₁,…,d_n)DP(d₁,…,d_n)1 всех n-ок допустимых значений переменных x₁,…,x_n, при которых предикат P(x₁,…,x_n) истинен.

Например, если P(x,y) есть x²y²13, а D_PNN, то M_P(2,3),(3,2).

Для одноместного предиката P(x) множество истинности есть множество M_PdD_PP(d)1допустимых значений переменной x, при котором предикат P(x) истинен.

Например, если P(x) есть x²13, а D_PN, то M_P1,2,3.

Используя связки , , , , , из данных предикатов P(x₁,…,x_n) и Q(x₁,…,x_n) с общей областью определения D образуются новые предикаты с той же областью определения D.

Отрицание P(x₁,…,x_n) строится из P(x₁,…,x_n) при помощи связки , при этом для любой n-ки (a₁,…,a_n)D.

Дизъюнкция P(x₁,…,x_n)Q(x₁,…,x_n) образуется из P(x₁,…,x_n) и Q(x₁,…,x_n) при помощи связки , при этом для любой n-ки (a₁,…,a_n)D

Конъюнкция P(x₁,…,x_n)Q(x₁,…,x_n) составляется из P(x₁,…,x_n) и Q(x₁,…,x_n) при помощи связки , при этом для любой n-ки (a₁,…,a_n)D

Легко увидеть, что , и .

Импликация P(x₁,…,x_n)Q(x₁,…,x_n) получается из P(x₁,…,x_n) и Q(x₁,…,x_n) при помощи связки , при этом для любой n-ки (a₁,…,a_n)D

Эквивалентность P(x₁,…,x_n)Q(x₁,…,x_n) строится из P(x₁,…,x_n) и Q(x₁,…,x_n) при помощи связки , при этом для любой n-ки (a₁,…,a_n)D

Для предикатов, кроме пропозициональных операций , , , , , существует операции навешивания кванторов.

Знак  обозначает слова вида "существует", "некоторые" и т.п.

Знак  обозначает слова вида "все", "для всякого" и т.п.

Квантор существования и общности – это символы x и x с некоторой переменной x.

Навешивание квантора x_i или x_i (i1,…,n) к предикату P(x₁,…,x_n), с n свободными переменными x₁,…,x_n, приводит, соответственно, к предикату x_iP(x₁,…,x_n) или x_i(x₁,…,x_n) уже с n1 свободными переменными x₁,…,x_i1,x_i1,…,x_n (переменная x_i станет связанной).