Лекция №13.

Тема: ТОЖДЕСТВЕННО ИСТИННЫЕ ПРЕДИКАТЫ

Основные вопросы, рассматриваемые на лекции:

1. Области определения и множества истинности отрицания P

2. Области определения дизъюнкции и конъюнкции P иQ

3. Множества истинности дизъюнкции и конъюнкции P иQ

4. Множества истинности импликации и эквивалентности P иQ

5. Области определения и множества истинности обощения и подтверждения

6. Тождественно истинные предикаты

Краткое содержание лекционного материала

Отрицанием предиката P(x₁,…,x_n) называется предложение "Неверно, что P(x₁,…,x_n)". Обозначение: P(x₁,…,x_n). Область определения предиката P совпадает с множеством UU₁…U_n – областью определения предиката P. При замене переменных x₁,…,x_n их допустимыми значениями a₁U₁, …, a_nU_n отрицание предиката обращается в отрицание высказывания, истинностное значение которого определяется по условию:

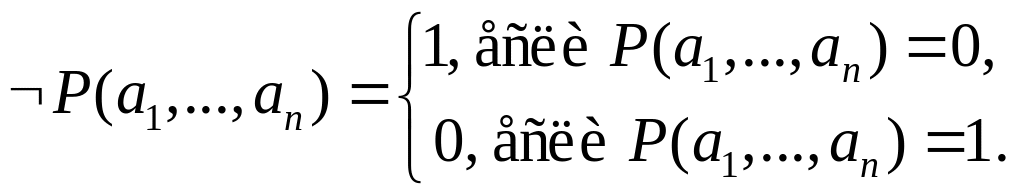
Множеством истинности предиката P является дополнение множества истинности предиката P до U: T_PU T_P.

Характеристическую функцию предиката P можно выразить через характеристическую функцию предиката P: _P1_P.

Пусть P(x₁,…,x_m,x_m1,…,x_mn) и Q(x_m1,…,x_mn,x_mn1,…,x_mns) – предикаты с общими переменными x_m1,…,x_mn. U₁, …, U_nns Далее мы в некоторых случаях для краткости переменные у предикатов не указываем.

Дизъюнкцией (конъюнкцией, импликацией, эквивалентностью) двух предикатов P(x₁,…,x_m,x_m1,…,x_mn) и Q(x_m1,…,x_mn,x_mn1,…,x_mns) называется предложение "P или Q" (соответственно, "P и Q", "если P, то Q", " P тогда и только тогда, когда Q"). Обозначение: (PQ)(x₁,…,x_mns)

P(x₁,…,x_m,x_m1,…,x_mn)Q(x_m1,…,x_mn,x_mn1,…,x_mns) (аналогично в остальных случаях). Пусть U₁, …, U_nns – множества допустимых значений переменных x₁, …, x_mns соответственно. Тогда UU₁…U_nns – область определения предиката PQ.

При замене переменных x₁,…,x_nns их допустимыми значениями a₁U₁, …, a_nns U_nns дизъюнкция, конъюнкция, импликация, эквивалентность двух предикатов обращается соответственно в дизъюнкцию конъюнкцию, импликацию, эквивалентность двух высказываний, истинностное значение которых определяется следующим образом:

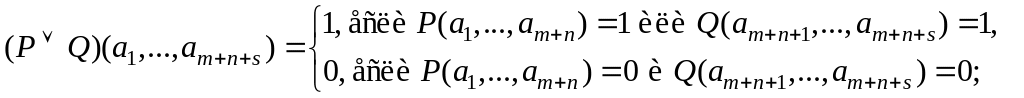
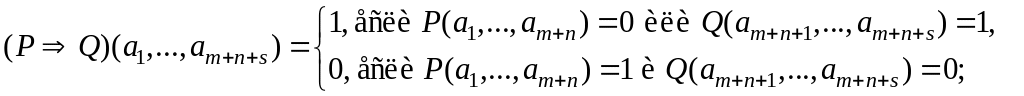
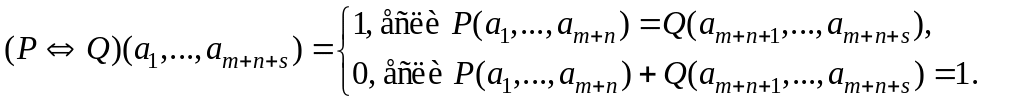
Рассмотрим для простоты предикаты P и Q с одними и теми же свободными переменными x₁,…,x_n и с одним и тем же множеством допустимых значений UU₁…U_n. Тогда множеством истинности дизъюнкции, конъюнкции, импликации и эквивалентности предикатов P и Q представляются через множества истинности предикатов P и Q следующим образом:

T_PQT_PT_Q, T_PQT_PT_Q, T_PQ(U T_P)T_Q,

T_PQ((U T_P)T_Q)(T_P(U T_Q)).

Характеристические функции предиката дизъюнкции, конъюнкции, импликации и эквивалентности предикатов P и Q можно выразить через характеристические функции предикатов P и Q следующим образом:

_PQ_P_Q_P_Q, _PQ_P_Q, _PQ1_P_P_Q,

_PQ1_P_Q2_P_Q.

В логике предикатов, кроме операций алгебры высказываний, рассматриваются операции навешивания кванторов.

Во-первых, кванторы – это символы  (все) и  (существует).

Во-вторых, кванторы – это слова вида "Для всех x" и "Существует x, такое, что", которые обозначаются соответственно x и x.

Пусть AP(x₁,…,x_n) – предикат с областью определения UU₁…U_n. Обобщением (подтверждением) P(x₁,…,x_n) по переменной x называется предложение вида "Для всех x верно, что A" (соответственно, "Существует x, такое, что A"). Эти предикат обозначается xA (xA). Предикаты xA и xA содержат n1 свободных переменных, если xx₁,…,x_n (переменная xx_i, где i1, …, n, становится связанной), и содержат n свободных переменных x₁,…,x_n, если xx₁,…,x_n.

Если xx₁,…,x_n, то при замене переменных x₁,…,x_n их допустимыми значениями a₁U₁, …, a_nU_n предикаты xA, xA и A обращаются в высказывания, истинностные значения которых равны:

P(a₁,…,a_n)xP(a₁,…,a_n)xP(a₁,…,a_n).

Если xx_i, где i1, …, n, то истинностные значения xA и xA при замене переменных x₁,…,x_i1,x_i1,…,x_n их допустимыми значениями a₁U₁, …, a_i1U_i1, a_i1U_i1, …, a_nU_n обращаются в высказывания, истинностные значения которых определяется следующим образом:

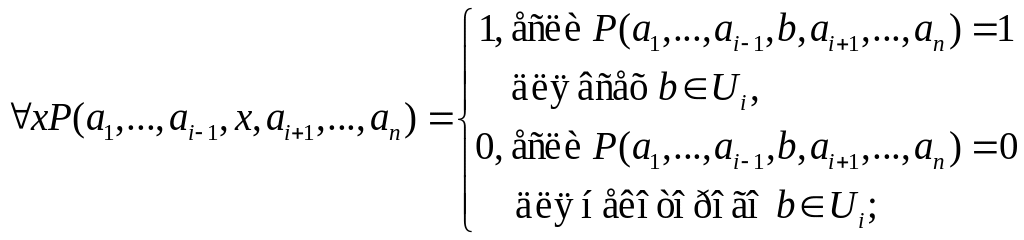
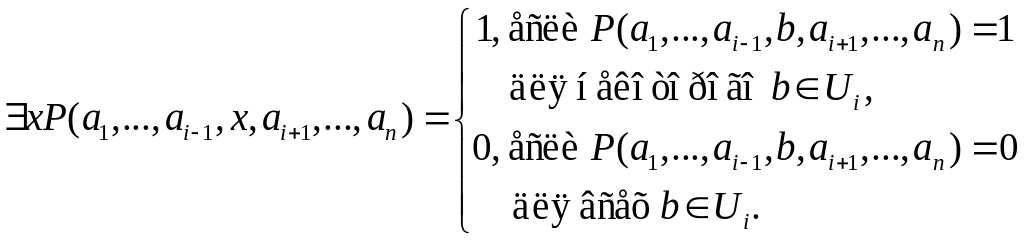
Терм t допустим для подстановки в формулу A вместо переменной x, если в A нет подформул вида yB для всех переменных y из t, отличных от x.

Пусть P(x₁,…,x_n) – предикат с областью определения UU₁…U_n. Говорят, что:

P(x₁,…,x_n) – тождественно истинный (или истинный) на множестве U предикат, если P(a₁,…,a_n)1 для всех a₁U₁, …, a_nU_n;

P(x₁,…,x_n) – тождественно ложный (или ложный) на множестве U предикат, если P(a₁,…,a_n)0 для всех a₁U₁, …, a_nU_n;

P(x₁,…,x_n) – выполнимый на множестве U предикат, если P(a₁,…,a_n)1 для некоторых a₁U₁, …, a_nU_n;

P(x₁,…,x_n) – опровержимый на множестве U предикат, если P(a₁,…,a_n)0 для некоторых a₁U₁, …, a_nU_n.

Высказывание xP(x) истинно (ложно), если P(x) – тождественно истинный (опровержимый) предикат. Высказывание xP(x) истинно (ложно), если P(x) – выполнимый (тождественно ложный) предикат.

Пример 1. Равенство xyyx является тождественно истинным предикатом на множестве UU₁U₂, если U₁U₂R – поле действительных чисел, но является опровержимым предикатом, если за U₁, U₂ – множества всех квадратных матриц порядка 2 над полем R.

Пример 2. Свойство линейности порядка тождественно истинный предикат на множестве URR, где отношение есть , и опровержимый предикат на множестве U2^M2^M, где 2^M – множество всех подмножеств некоторого множества M, где отношение есть .

Примеры 1 и 2 показывают, что свойство тождественной истинности предиката на множестве U существенно зависит от структуры операций и отношений, определенных на множестве U.

Пример 3. Предложение x y xy является тождественно истинным предикатом на любом множестве вида UU₁U₂. Предложение x y xy является тождественно истинным предикатом на любом множестве вида Uab и является опровержимым предикатом на любом множестве вида UU₁U₂, если U₁U₂ содержит не менее двух элементов.

Пример 4. Импликация (x P(x)x Q(x))x (P(x)Q(x)) является тождественно истинным предикатом на любом множестве U для любых предикатов P(x) и Q(x). Импликация (x P(x)x Q(x))x (P(x)Q(x)) является опровержимым предикатом, например, на множестве UR, если P(x) есть x100 и Q(x) есть x90.

Примеры 3 и 4 показывают, что свойство тождественной истинности предиката существенно зависит от формы построения предиката при помощи логических связок и кванторов.