§ 6.9. Коды боуза — чоудхури — хоквингема

Математическое введение. Рассматриваемые циклические коды, сокращенно называемые БЧХ - кодами, составляют большой класс кодов, предназначенных для исправления независимых ошибок произвольной кратности s. Их минимальное кодовое расстояние, следовательно, должно быть не менее чем d_min = 2s + 1.

Для понимания математической структуры БЧХ - кодов необходимо ознакомиться с некоторыми новыми понятиями линейной алгебры. В общем случае эти понятия справедливы для множества многочленов с коэффициентами из поля GF(q), где q — простое число. Поскольку нас интересуют в первую очередь двоичные коды, мы ограничимся случаем q = 2.

Ранее было рассмотрено разложение кольца на классы вычетов по идеалу (см. табл. 6.10). Если в качестве образующего многочлена идеала g(x) взят неприводимый многочлен степени т, принадлежащий показателю степени n(n = 2^m—1), то общее число классов вычетов, включая идеал, равно 2^m.

Зададим операции сложения и умножения для полученных классов вычетов:

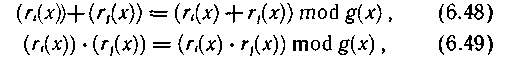
где (ri(х)) — класс вычетов по модулю многочлена g(x) содержащий элемент ri(x).

При этом совокупность классов вычетов образует конечное поле. Оно насчитывает 2^m элементов, обозначается GF(2^m) и называется расширением поля степени m над GF(2). Единичным и нулевым элементами поля являются классы вычетов соответственно (1) и (0).

Нетрудно убедиться в том, что для любого ненулевого элемента поля (г_a(х)) в нем найдется обратный ему элемент (r_a(х)), удовлетворяющий равенству

Пример 6.22. Построим поле порядка 24, используя неприводимый многочлен g(x) = x⁴ + x + 1 ·

Полная совокупность классов вычетов равна числу остатков, получающихся при делении произвольного многочлена на многочлен р(х). Для заданного многочлена эта совокупность составляет 16 классов вычетов: (0), (1), (x), (х+1), (х²), (х²+1), (х²+х), (х²+х+1), (х³), (х³+1), (х³+х), (х³+х²), (х³+х+1), (х³+х²+1), (х³+х²+х), (х³+х²+х+1).

Поскольку построение таблицы сложения элементов поля трудностей не представляет, ограничимся записью таблицы умножения этих элементов. Обозначив через α класс вычетов (х), содержащий многочлен х, и исключив из рассмотрения нулевой элемент, получим табл. 6.22.

Таблица 6.22

Из приведенного примера видно, что составление таблицы умножения элементов поля, представленных многочленами, является достаточно трудоемким делом. Однако процедура умножения существенно упрощается благодаря возможности представления всех элементов поля в виде степеней одного из его элементов.

Доказано, что в любом конечном поле найдется по крайней мере один элемент α, такой, что все ненулевые элементы поля могут быть представлены в виде различных степеней αⁱ этого элемента, называемого примитивным элементом поля. Так как рассматриваемое поле конечно и насчитывает n=2^m-1 ненулевых элементов, то начиная с αⁿ = 1 элементы поля начнут повторяться.

Элементы поля могут быть выражены и через отрицательные степени α , так как поле содержит мультипликативный обратный элемент каждого ненулевого элемента. Используя элементы α^m-1, α^m-2, ..., α, 1 в качестве базиса, элементы поля можно представить также в виде двоичных последовательностей (векторное представление).

Пример 6.23. Приведем различное представление элементов поля, построенного на основе неприводимого многочлена g(x) = х⁴ + х+1 (табл. 6.23).

Таблица 6.23

Выражение элементов через отрицательную степень α осуществляется делением на α¹⁵ = 1.

Покажем теперь, что любой элемент конечного поля порядка 2^m является корнем уравнения

Для ненулевых элементов поля соответственно имеем

Если α — примитивный элемент поля, то произвольный ненулевой элемент представляется в виде степени а, т. е. β = αⁱ.

Тогдаи, следовательно, все ненулевые элементы поля являются корнями уравнения хⁿ + 1 = 0. Эти корни принадлежат различным неприводимым в поле GF(2) многочленам, на которые разлагается двучлен xⁿ +1. Алгоритм такого разложения был приведен ранее. В частности, в примере 6.13 получена совокупность многочленов, корнями которых являются элементы поля Gf(24):

Для нас существенно, как распределены корни двучлена xⁿ+1 (а следовательно, и элементы поля) по составляющим неприводимым многочленам. Доказана следующая закономерность. Если известен один из корней β неприводимого многочлена степени m, то все другие корни этого многочлена являются определенными степенями β, а именно:

Порядок корней неприводимого многочлена является показателем, которому этот многочлен принадлежит.

Многочлен g(x) наименьшей степени, такой, что g(β)=0, называется минимальным многочленом для элемента β. Будем обозначать его gβ(x). Неприводимый над полем GF(2) многочлен степени т называется примитивным, если его корнем является примитивный элемент поля GF(2^m).

Пример 6.24. Найдем распределение корней двучлена

Если корни рассматривать как элементы поля, построенного с использованием неприводимого многочлена g(x) = x⁴ + x + 1, то этот многочлен является примитивным Действительно, примитивный элемент α поля GF(2⁴) является корнем многочлена g(x). Остальные его корни соответственно равны α² , α⁴ и α⁸. Можно непосредственно убедиться в справедливости равенства

Теперь найдем минимальный многочлен g3(x) для элемента α³. Его корнями должны быть элементы

откуда

Аналогично определим минимальные многочлены g5(x) и g7(x) для элементов α⁵ и α⁷. Цикл корней g5(x) включает α⁵ и α¹⁰ соответственно для g7(x) имеем α⁷, α¹⁴, α¹³, α¹¹.

Следовательно,

Итак, распределено 14 корней многочлена x¹⁵+ 1. Последний кореньα⁰равен 1 и принадлежит двучленуx+ 1.

Построение и реализация кодов. Процесс выбора образующего многочлена кода Боуза — Чоудхури — Хоквингема, рассчитанного на исправление единичных ошибок, ничем не отличается от рассмотренного ранее. Основное отличие заключается в интерпретации опознавателей ошибок. В данном случае ими считаются различные степени примитивного элемента поля GF(2^m), построенного с использованием выбранного неприводимого многочлена g(x) степени m, принадлежащего показателю степени n = 2^m—1. Так как число различных ненулевых элементов поля, выраженных степенями примитивного элемента, равно n, то каждому вектору ошибки в отдельном разряде можно сопоставить свой опознаватель, что и гарантирует возможность исправления ошибок.

При возникновении двух ошибок построенный код позволяет определить только сумму s опознавателей этих ошибок

где ξ, и ξ, — опознаватели ошибок в разрядах i и j.

Для однозначного определения ошибок необходимо еще одно независимое уравнение. Возможно использование степенных функций от ξ. Однако квадраты опознавателей не приводят к желательному результату, поскольку второе уравнение с учетом сложения по модулю два оказывается квадратом первого.

Действительно,

Если использовать кубы опознавателей, то уравнения оказываются независимыми

Такой подход допускает обобщение на случай исправления 3- и 4-кратных ошибок и т. д. При этом к полученным уравнениям соответственно добавляются уравнения с опознавателями в пятой, седьмой степенях и т. д.

Коснемся подробнее случая исправления двойных ошибок. Проведем преобразование второго уравнения

откуда

Поскольку известны сумма и произведение опознавателей, то на основании теоремы Виета можно составить уравнение, для которого опознаватели ξ_i и ξ_j являются корнями:

Если ошибка оказалась одна, то

и ее опознаватель удовлетворяет уравнению

При отсутствии ошибок, естественно, получаем нулевые опознаватели, так как s₁=s₃ = 0.

На практике оказывается удобнее использовать многочлены, корнями которых являются не опознаватели ошибок, а их мультипликативные обратные элементы z= =ξ^-1.

Для случая исправления двойных ошибок левая часть уравнения преобразуется к виду

При возникновении одной ошибки

при отсутствии ошибок

Осталось выяснить, как получить суммы нечетных степеней опознавателей ошибок, в частности сумму 5з кубов опознавателей при исправлении двойных ошибок. Указанные суммы можно определить за счет последовательного добавления к выбранному примитивному многочлену g(x) в качестве сомножителей минимальных многочленов для элементов α³ (случай двойных ошибок), α⁵ (случай тройных ошибок) и т. д. Суммы нечетных степеней опознавателей ошибок вычисляются по остаткам, получаемым в результате деления принятой кодовой комбинации на соответствующий минимальный многочлен.

В общем случае образующий многочлен кода Боуза — Чоудхури — Хоквингема представляет собой наименьшее общее кратное (НОК) примитивного и минимальных многочленов

В частности, для кода с n =15, рассчитанного на исправление двойных независимых ошибок, получаем

Пример 6.25. Рассмотрим процесс исправления единичных ошибок кодом Боуза — Чоудхури (15, 11) с образующим многочленом g(x) = x⁴ + x + 1.

Используя табл. 6.23, сопоставим каждому вектору ошибки свой опознаватель в виде определенной степени примитивного элемента ее поля GF(2⁴) Результат представлен табл. 6.24.

Таблица 6.24

Схема декодирующего устройства представлена на рис 6.24. Детектор ошибки выполнен в соответствии с уравнениемl+s1z = 0. За первые n = 15 тактов в результате деления поступающей из канала связи кодовой комбинации h(x) на g(x) получаем в регистре I опознаватель ошибки х^-j. Затем он переписывается в регистр II схемы, осуществляющей домножение опознавателя на α с приведением по модулю g(x), тес превращением α⁴ в α + 1.

На (n + 1)-м такте символ старшего разряда кодовой комбинации h(x) поступает из буферного регистра в сумматор коррекции. Одновременно производится домножение опознавателя α^-j на α, и на схему ИЛИ детектора подается вектор 1+si*α. Если 1 +s₁ α неравно 0, то s₁ неравно α^-1 и, следовательно, ошибка произошла не в старшем разряде.

Аналогично анализируется правильность других символов, последовательно поступающих в узел коррекции из буферного регистра. Когда в схеме коррекции появляется искаженный символ j-и позиции (начиная со старшего разряда), то 1+ +s₁α^j = 0 и s₁ = α^-j. При этом выходной сигнал схемы ИЛИ детектора равен нулю и импульс с выхода схемы НЕ корректирует ошибку.

Пример 6.26. Наметим последовательность операций при исправлении двойных ошибок кодом (15, 7) с образующим многочленом g(x) = (x⁴ + x + 1)(x⁴ + x³ + x² + x + 1).

В процедуре декодирования указанного кода можно выделить следующие этапы:

1) нахождение суммы s₁ опознавателей ошибок путем деления поступившей из канала связи кодовой комбинации h(x) на многочлен х⁴ + x + 1;

2) определение суммы s3 кубов опознавателей в базисе α⁹ α⁶ α¹ путем деления h(x) на многочлен х⁴ + х³ + x² + x + 1;

3) выражение s₃ в базисе α³ α² α1;

4) вычисление s₁², отношения s₃/s₁ и суммы s₁² + s₃/s₁,

5) построение схемы для определения корней уравнения q(z) = 1+s₁z+(s₁² + + s₃/s₁)z² путем последовательного домножения s1 на α и (s₁² + s₃/s₁) на α².