§ 2.5. Методы дискретизации посредством выборок

При построении метода дискретизации необходимо сформулировать критерий выбора отсчетов, установить процедуру восстановления по ним исходного сигнала и иметь возможность определить возникающую при этом погрешность. Решение указанных задач возможно лишь на базе выбора определенной математической модели дискретизируемого сигнала.

В вопросе определения величины шага при равномерной дискретизации известно несколько подходов, отличающихся, прежде всего тем, каким параметром характеризуются динамические свойства сигнала.

В теоретических исследованиях наибольшее распространение получила модель сигнала в виде квазистационарного случайного процесса, каждая реализация которого представляет собой функцию с ограниченным спектром. Величина шага дискретизации в этом случае ставится в зависимость от наивысшей частоты спектра. Такой критерий выбора отсчетов принято называть частотным.

При определении шага дискретизации можно ориентироваться непосредственно на степень некоррелированности отсчетов. Существует подход, где за модель

сигнала принят случайный процесс конечной длительности Т, спектр которого отличен от нуля на всей оси частот. В предположении, что ₀<<T,отсчеты берут через интервал корреляцииτ₀, определяемый по известной корреляционной функции сигнала. Такой критерий выбора отсчетов называют корреляционным. Учитывая тесную взаимосвязь спектрального и корреляционного методов анализа сигналов, его иногда рассматривают как разновидность частотного критерия. Поскольку использование корреляционного критерия по сравнению с частотным не упрощает теоретических исследований, он не нашел применения в инженерной практике.

Практическую реализацию равномерной дискретизации чаще всего проводят с использованием аппроксимирующих многочленов в общем случае n-й степени. За математическую модель сигнала принимают стационарный случайный процесс, каждая реализация которого представляет собой непрерывную функцию u(t), имеющую (n+1) ограниченных производных. При этом динамические свойства сигнала задаются максимальным во всем интервале преобразования модулем (n+1)-й его производной. Отсчеты выбирают по критерию наибольшего отклонения.

Так как при равномерной дискретизации шаг выбирают, исходя из максимальных значений динамических характеристик сигнала, то на многих участках интервала дискретизации, где мгновенные значения сигнала резко не меняются, он оказывается заниженным, что приводит к избыточности отсчетов.

Эффективное устранение избыточности в отсчетах обеспечивают методы адаптивной неравномерной дискретизации. Длительности шагов дискретизации в этом случае тесно связаны с текущими значениями параметров реализации сигнала. Отсчеты проводятся при достижении выбранной погрешностью восстановления определенного значения, выполняющего здесь роль критерия.

Основные методы дискретизации по выборкам рассмотрим подробнее.

§ 2.6. Равномерная дискретизация. Теорема котельникова

Дискретизация по частотному критерию. Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром в наиболее четкой форме сформулировано и доказано акад. В. А. Котельниковым в виде теоремы, получившей в отечественной литературе его имя* [11].

Сначала, не касаясь вопроса адекватности выбранной модели реальному сигналу, рассмотрим существо и доказательство теоремы

Теорема Котельникова. Теорема устанавливает принципиальную возможность полного восстановления детерминированной функции с ограниченным спектром по ее отсчетам и указывает предельное значение интервала времени между отсчетами, при которой такое восстановление еще возможно. Она формулируется следующим образом: функция u(t), допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от 0 до F_c = _c/(2), полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервалы времени

Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной ее спектра. Только в случае, когда спектр функции безграничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно (корреляционная связь между ними отсутствует). Сокращение высокочастотной части спектра до граничной частоты ω₁ равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими (рис. 2.2, а). При меньших граничных частотах ₂ (рис. 2.2, б) и ₃ (рис. 2.2, в) имеем более сглаженные функции времени. Поскольку значения этих функций в моменты времени u(t₁) и u(t₁+t)в пределах некоторого интервала Δt не могут изменяться существенно, можно ограничиться значениями функции, взятыми через интервалы Δt (отсчетами).

Д о к а з а т е л ь с т в о. Пусть функции u(t), описывающей передаваемый сигнал, соответствует спектральная характеристика S(j), причем

где _c — наибольшая частота спектра u(t).

Используя обратное преобразование Фурье с учетом соотношения (2.13), запишем

Для моментов времени t_n = nΔt = n/_c, где n — любое целое число, функция u(t) принимает значения

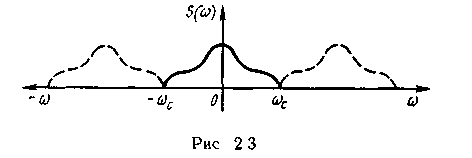
Функцию S(j) на интервале существования от - _c до +_c можно разложить в ряд Фурье по частотам, периодически продолжая ее с периодом 2_c (рис. 2.3):

где

Сравнивая (2.15) и (2.16), найдем

Выразим теперь S(j) через отсчеты исходной функции:

Поскольку суммирование ведется как по положительным, так и по отрицательным числам n, знак перед n можно изменить на обратный:

Подставив это значение в (2.14), определим значения исходной функции в любой момент времени:

Учитывая сходимость ряда Фурье, изменим порядок суммирования и интегрирования:

В полученном выражении вычислим интеграл:

Подставив результат в формулу (2.18), окончательно получим

Итак, функция u(t) выражена через ее дискретные значения, взятые в моменты времени t_n = nt= n/_c.

Так как при любых целых k и n справедливы соотношения

то

Благодаря этому свойству значения функции u(k) в моменты времени tn = ntпредставляют собой нечто иное, как ее отсчеты.

Представление функции u(t) в виде ряда (2.19) (ряда Котельникова) является частным случаем разложения (1.1). Роль коэффициентов C_k выполняют отсчеты u(nt)функции u(t). Базисными являются функции вида

Они называются функциями отсчетов.

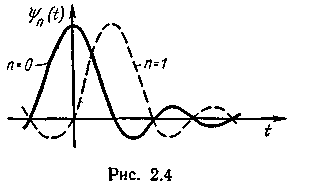
Графики этих функций при n = 0 и n = 1 приведены на рис. 2.4. Каждая функция ψ_n(t) имеет неограниченную протяженность во времени и достигает своего наибольшего значения, равного единице, в момент времени t = n/_c; относительно этого момента времени она симметрична. В моменты времени t=r/_c, где kn, функция обращается в нуль. Все функции ортогональны между собой на бесконечно большом промежутке времени, что легко проверяется путем вычисления интеграла:

Каждую функцию отсчета можно рассматривать как реакцию (отклик) идеального фильтра нижних частот с граничной частотой F_c на дельта-импульс, приходящий в момент времени t_n = ntи имеющий площадь, равную u(nt).

Теорема Котельникова распространяется на непрерывный в среднеквадратическом смысле стационарный случайный процесс с ограниченным энергетическим спектром (S_n() = 0 при |ω|>ω_П = 2F_П).

Такой процесс представляется суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов — величины выборок:

где

Таким образом, при указанных ограничениях случайный процесс полностью определяется счетным множеством случайных величин — координат процесса.

Пример 2.1. Определить по теореме Котельникова шаг дискретизации Δ< для детерминированной функции

ориентируясь на практическую ширину спектра (1.60) с η = 0,95. По формуле (1 42) находим спектральную характеристику

откуда

Практическую ширину спектра определяем, пользуясь соотношением (1.60).

Поскольку

имеем

По таблице значений тангенсов получаем

Следовательно,