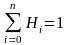16. Квадратурная формула Ньютона-Котеса

Формула Ньютона – Котеса:

(1)

где , i = 0, 1, 2,…, n -- коэффициенты Ньютона – Котеса, 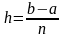- шаг разбиения интервала [a, b] на n точек.

Для коэффициентов Ньютона – Котеса справедливы следующие соотношения:

1. 

2. 

Недостатком метода Ньютона-Котеса является то, что при большихn в формуле (1) будут встречаться как положительные, так и отрицательные коэффициенты H_i, превосходящие по абсолютной величине достаточно большое число. При больших n могут появиться большие погрешности при вычислении интегралов. Поэтому формулы Ньютона-Котеса малопригодны для вычислений, когда число узлов n велико.

Пример.

Вычислить интеграл методом Ньютона – Котеса.

Интервал [1, 2] разобьем на n = 5 точек, шаг разбиения

Тогда, согласноформуле (1), будемиметь

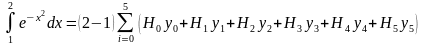
По свойствам коэффициентов Ньютона-Котеса

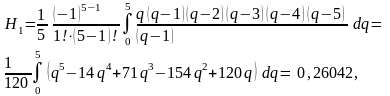
Далее вычислим значения подынтегральной функции в точках x_i, i = 0, 1, 2, 3, 4, 5.

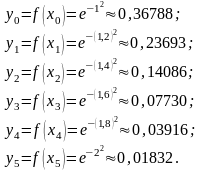
Учитывая свойства коэффициентов Ньютона-Котеса, можем записать

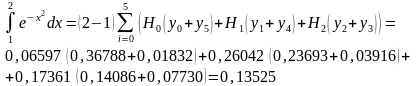
= 0,13525

16. Квадратурная формула Гаусса

(используется для интегрирования функции, имеющей аналитическое выражение)

Пусть необходимо вычислить интеграл вида

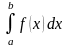
Квадратурная формула Гаусса имеет вид 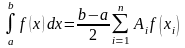(1)

где , (i = 1, 2,…, n), (2)

t_i - нули полинома Лежандра P_n(t), т. е. P_n(t_i) = 0.

Для коэффициентов A_i и узлов t_i существуют справочные таблицы.

Формула Гаусса обеспечивает наивысшую точность в том смысле, что для полиномов степени не выше 2n-1 она точна.

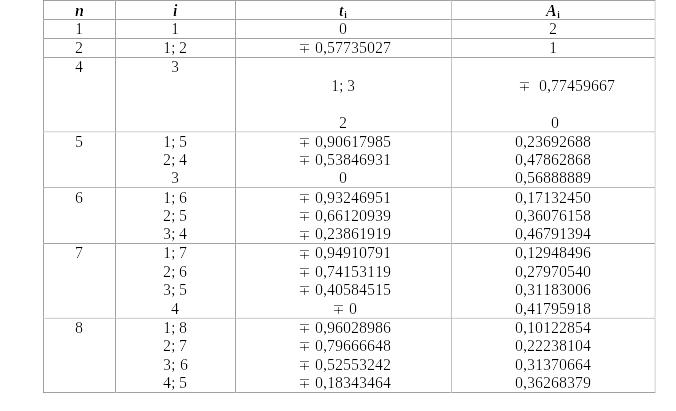
Коэффициенты A_i и узлы t_i для численного интегрирования по формуле Гаусса.

Пример.

Применяя квадратурную формулу Гаусса, вычислить интеграл .

Разобьем интервал [1, 2] на n = 5 точек и для вычисления интеграла воспользуемся полиномом Лежандра 5-й степени .

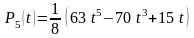Делаем замену переменной ,

где 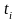- корни (нули) полинома Лежандра , т. е. .

Из таблицы 1 возьмем значения корней и коэффициентов :

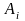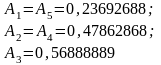
Тогдаможемзаписать

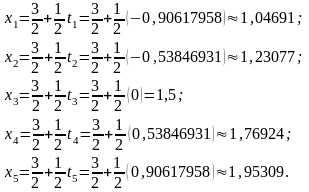
Далее вычислим значение подынтегральной функции

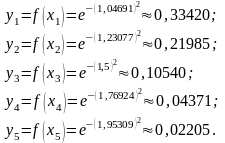
Согласноформуле (.2) получаем

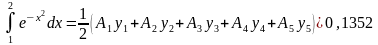
16. Численные метода решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Эйлера-Коши

Задача Коши состоит в нахождении решения y = y(x) , удовлетворяющего начальным условиям 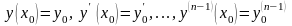(1)

где 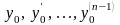заданные числа. Условия (1) для задачи Коши задаются в одной точке . Для граничных задач дополнительные условия задаются не в одной, а в нескольких точках.

Численные методы используются в задачах, имеющих единственное решение (т.е. корректно поставленных). В некоторых случаях условий корректности может оказаться недостаточно. Необходимо, чтобы задача была хорошо обусловлена (устойчива), т. е. малые изменения в задании исходных данных приводили к достаточно малым изменениям искомого решения.

Метод Эйлера

Метод Эйлера - один из самых простых методов численного решения дифференциальных уравнений. Его недостаток - сравнительно низкая точность.

Пусть дано дифференциальное уравнение

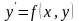(2)

с начальным условием 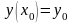(3)

Численное решение задачи Коши (5.3)-(5.4) состоит в том, чтобы получить искомое решение y = y(x) в виде таблицы его приближенных значений для заданных значений аргумента x на некотором отрезке [a, b]: а = x₀<x₁< ... <x_n = b. Точки называются узловыми точками, а множество этих точек называют сеткой на [a, b].

Выбираем малый шаг h и на отрезке [a, b] строим систему равноотстоящих точек

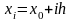, (i = 0, 1, 2,…, n). (4)

В методе Эйлера искомая интегральная кривая y = y(x) , проходящая через точку (x₀,y₀), приближенно заменяется ломаной с вершинами (x_i,y_i) , звенья которой прямолинейны между прямыми и имеют подъем с начальным условием

(5) Таким образом, каждое значение y_i+1 можно найти по формуле

, (i = 0, 1, 2,…, n) (6)

В результате, получим совокупность значений 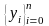численного решения задачи Коши.

В каждом узле x_i имеем y_i»y(x_i) , (i = 0, 1, 2,…, n). Причем для любого численного метода начальные условия задачи Коши выполняются точно, т. е. y(x₀) = y₀

Метод Эйлера может применяться для решения обыкновенных дифференциальных уравнений высших порядков и для систем дифференциальных уравнений.

Рассмотрим систему дифференциальных уравнений первого порядка

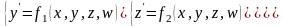
с начальными условиями

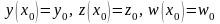
Решения задачи Коши для данной системы уравнений можно получить, используя следующие формулы

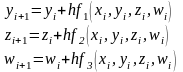
Пример.

Найти решение задачи Коши , на отрезке [1; 1,5]

Применим метод Эйлера. Сделав замену переменных y’ = z, z’ = w , понизим порядок уравнения. Из исходного уравнения получаем систему дифференциальных уравнений первого порядка:

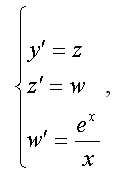с начальными условиями

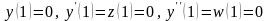
Cоответствующие формулы метода Эйлера имеют вид

где

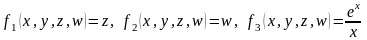
Интервал [1; 1,5] разобьем на 5 точек с шагом разбиения

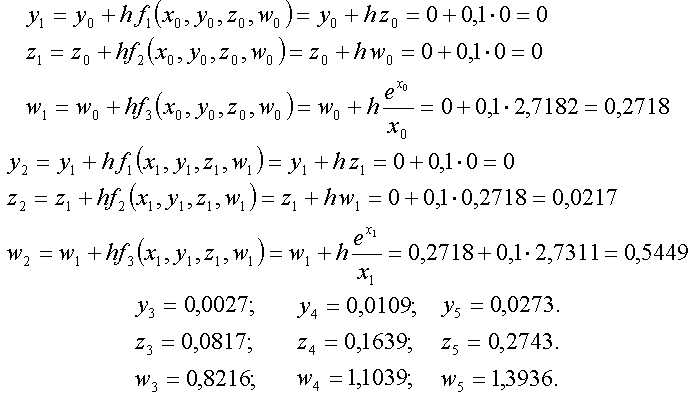
Метод Эйлера применяется редко, однако при дальнейшем рассмотрении мы будем на него ссылаться