Метод конечных разностей численного решения обыкновенных дифференциальных уравнений.
(метод сеток)
По определению производная функции одной переменной имеет вид:
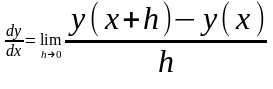
Компьютер не может совершить предельный переход.
Однако мы можем придать h малое (но не нулевое) значение и проверить, получается ли приближение достаточно точным (проблема точности) и что ошибка не возрастает в ходе вычислений (проблема устойчивости).
Метод сводится к тому, что производная заменяется разностью.
Метод сеток, или метод конечных разностей – один из самых распространенных методов численного решения уравнений с частными производными.
В основе – идея замены производных конечно-разностными отношениями.
Ограничимся случаем двух независимых переменных.
Пусть в плоскости xOy имеется некоторая область G с границей Г (Рис.6.1).
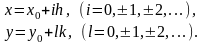
Построим
два семейства параллельных прямых: 
Точки пересечения прямых называют узлами. Два узла называют соседними, если они удалены вдоль оси Ox или Oy на шаг сетки h или k соответственно.
Узлы, принадлежащие G +Г и расположенные вне этой области на расстоянии, меньшем, чем шаг от Г, называют внутренними.
Оставшиеся из выделенных – граничные.
Рассмотрим сначала разности в направлении x.
Р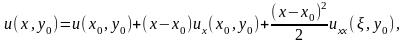
азложим
функцию u = u(x, y0) в ряд Тейлора в окрестности
точки x0, y0.
где ξ лежит между x и x0.
Е
сли
положить x = x0 + h, то можно получить
следующее выражение
Т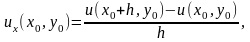
.е.
если представить ux с помощью
то ошибка ограничения будет равна
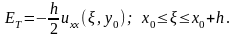
Равенство (6.1) получено с помощью подстановки x = x0 + h, результат называется правой разностью.
А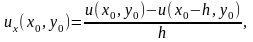
налогично
можно получить левую разность
П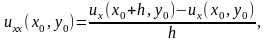
риближение
для uxx через правую разность
Е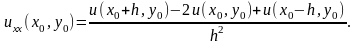
сли
в выражение (6.3) подставить правые
разности для ux, весь результат окажется
«сдвинутым» вправо. Для компенсации
используем левые разности для ux. Получим
Можно отметить симметрию полученной формулы относительно x0, y0.
Д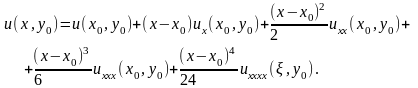
ля
определения ошибки ограничения вспомним,
что
П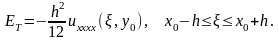
оложим
теперь x = x0+ h; x = x0 - h и сложим два равенства.
Получится, что ошибка ограничения равна
А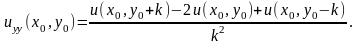
налогичный
анализ проводится для производных в
направлении y:
Здесь k -- величина шага по y.
О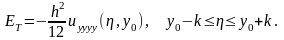
шибка
ограничения равна
С использованием полученных выражений можно полностью переписать дифференциальное уравнение в частных производных и перейти к уравнению в конечных разностях.
Принципы построения сеток на плоскости и в пространстве.
По определению производная функции одной переменной имеет вид:
Компьютер не может совершить предельный переход.
Однако мы можем придать h малое (но не нулевое) значение и проверить, получается ли приближение достаточно точным (проблема точности) и что ошибка не возрастает в ходе вычислений (проблема устойчивости).
Метод сводится к тому, что производная заменяется разностью.
В основе – идея замены производных конечно-разностными отношениями.
Ограничимся случаем двух независимых переменных.
Пусть в плоскости xOy имеется некоторая область G с границей Г (Рис.6.1).
П остроим два семейства параллельных прямых:
Точки пересечения прямых называют узлами. Два узла называют соседними, если они удалены вдоль оси Ox или Oy на шаг сетки h или k соответственно.
Узлы, принадлежащие G +Г и расположенные вне этой области на расстоянии, меньшем, чем шаг от Г, называют внутренними.
Оставшиеся из выделенных – граничные.
(в пространстве ничего не нашла)