26. Построение разностных схем для уравнений параболического типа.

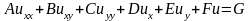
Параболические уравнения при B² - 4AC = 0.

Типичная физическая задача -- процесс теплопередачи по длинному стержню, лежащему вдоль оси х от х = 0 до х = L.

Предположим, что в точке х = 0 температура поддерживается на уровне Т0, а в точке х = L температура поддерживается на уровне TL.

Предположим также, что в момент времени t = 0 распределение температуры вдоль стержня задавалось функцией f(x).

Тогда распределение температуры вдоль стержня во все последующие моменты времени дается решением уравнения

u_xx = au_t, (7.16)

В уравнении (7.16) u – температура стержня в данной точке в данный

момент времени, постоянная а зависит от физических свойств стержня. Для простоты положим а = 1, так что уравнение сведется к виду:

u_xx = u_t, (7.17)

Граничные условия

u(0, t) = T0,

u(L, t) = TL. (7.18)

Начальное условие

u(x, 0) = f(x). (7.19)

Уравнение (7.17) представляет собой параболическое дифференциальное уравнение в частных производных.

Его называют уравнением теплопередачи или уравнением диффузии

При записи в разностной форме граничные условия (7.18) запишутся в виде

u₀, j = T0 ;j = 1, 2, …,

(7.20)

u_n, j = TL ; j = 1, 2, …,

Начальное условие имеет вид u_i, 0 = f(ih). (7.21)Чтобы преобразовать в разностную форму уравнение (7.17), введем сетку, охватывающую область 0 ≤ х ≤ L и t > 0 с интервалом разбиения h в направлении x и интервалом разбиения k в направлении t.

С использованием (6.1) и (6.3) получаем

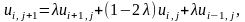
где

λ= k/h2. (7.23)

Выражении (7.22) индекс i изменяется от 1 до n - 1, а индекс j -- от 1 до ∞.

В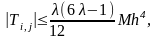 ерхний предел ошибки ограничения

где

|u_xxxx| < M

при условии λ≠1/6.

П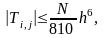 ри λ = 1/6

где

|u_xxxxxx| < N.

Рассмотрим теперь два других способа построения разностных схем

для параболического уравнения.

Р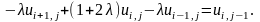 азностная схема (7.22) была получена с использованием правых разностей. Если же взять левые, получим

В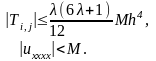 ерхний предел ошибки ограничения

Этот предел больше, чем в схеме (7.22); кроме того, нельзя свести ошибку ограничения к О(h6) специальным выбором параметра λ.

Рассмотрим еще один способ построения разностного уравнения, эквивалентного (7.22).

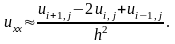
Согласно (6.4), в точке i, j

А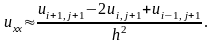 налогично в точке i, j + 1

У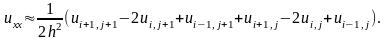 средняя, получим

Если теперь для вычисления ut воспользоваться правыми разностями, то

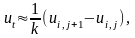
и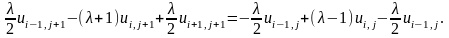 разностное уравнение, эквивалентное (7.17), запишется в виде

Этот способ построения разностного уравнения часто называют методом Кранка - Никольсона.

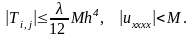
Верхний предел ошибки ограничения

Полученный верхний предел в (6 λ + 1) раз меньше, чем для схемы (7.17).

Поэтому разностное уравнение (7.25) предпочтительнее, чем (7.17).