
- •Приближенные числа
- •Правила вычислений с приближенными числами.
- •Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней и уточнение приближенных корней. Графическое решение уравнений.
- •Метод половинного деления (метод «вилки»).
- •Метод хорд.
- •Метод Ньютона (метод касательных).
- •Метод итерации. Приведение уравнений к виду, удобному для итерации.
- •Приближенное решение систем линейных уравнений. Метод итераций.
- •Приближенное решение систем нелинейных уравнений. Метод итерации.
- •Постановка задачи интерполирования функций. Общее решение задачи интерполирования функции полиномом.
- •Интерполяционная формула Лагранжа
- •Интерполирование сплайнами
- •14 Аппроксимирование функций (15 не нашли)
- •Аппроксимирование функций. Метод ортогональных функций.
- •Квадратурная формула Ньютона-Котеса
- •Квадратурная формула Гаусса
- •Численные метода решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Эйлера-Коши
- •Метод Рунге-Кутта
- •Редукция к задаче Коши двухточечной краевой задачи для линейного уравнения второго порядка.
- •Метод коллокации.
- •23.Аппроксимация производных конечно-разностными соотношениями.
- •Метод конечных разностей численного решения обыкновенных дифференциальных уравнений.
- •Принципы построения сеток на плоскости и в пространстве.
- •26. Построение разностных схем для уравнений параболического типа.
- •27. Экстремумы функций. Классификация методов безусловной оптимизации.
- •28. Общая характеристика методов оптимизации нулевого порядка.
- •Метод прямого поиска (метод Хука-Дживса).
- •Метод деформируемого многогранника (метод Нелдера-Мида).
- •Метод вращающихся координат (метод Розенброка).
- •Метод параллельных касательных (метод Пауэлла).
- •Общая характеристика методов оптимизации первого порядка.
- •34.Метод наискорейшего спуска
- •35. Общая характеристика методов оптимизации второго порядка. Метод Ньютона.
- •36. Метод Ньютона с регулировкой шага (метод с переменной метрикой)
- •37. Метод статистических испытаний (метод Монте-Карло)
- •38. Вычисление кратных интегралов методом Монте-Карло
- •39. Структура искусственной нейронной сети (инс)
- •40. Компьютерная модель нейрона (нейроэлемента, нэ)
- •41. Функции активации нейроэлементов
- •45.Методы обучения элементарного перцептрона.
- •46.Многослойный перцептрон.
- •47. Понятие обучающей выборки.
28. Общая характеристика методов оптимизации нулевого порядка.
В этих методах:
не надо вычислять производные целевой функции;
направление минимизации полностью определяется последовательными вычислениями значений функции;
можно работать с функциями, имеющими разрывные производные (при этом другие методы не подходят);
критерий оптимальности может быть задан не в явном виде, а системой уравнений;
сходимость обычно медленнее, чем у методов первого и второго порядков
Кроме того,
вычисление первых и вторых производных функции многих переменных бывает очень трудоемким;
часто они не могут быть получены в виде аналитических функций;
определение производных с помощью численных методов сопровождается ошибками.
Метод прямого поиска (метод Хука-Дживса).
Идея метода:
задается начальная точка x[0];
путем изменения компонент вектора x[0] исследуются окрестности начальной точки;
если найдено направление, в котором функция уменьшается, производится спуск в этом направлении;
если нет, -- уменьшается величина шага;
если дробление шага не дает результата, от выбранного направления отказываются и выполняется новое исследование окрестности.
Алгоритм.
1. Задаются значениями координат xi[0] (i = 1, 2, …, n) начальной точки x[0], вектором изменения координат Dx, точностью e для Dx.
2. Полагают, что x[0] является базисной точкойxB, вычиcляют значение f(xB).
3. Циклически меняют каждую координату xiB базисной точки xB на величинуDxi , т.е.
xi[k] = xiB+ Dxi ; xi[k] = xiB- Dxi i = 1, 2, …, n.
При этом вычисляют f(x[k]) и сравнивают с f(xB). Если f(x[k]) <f(xB), то соответствующая координата xi получает новое значение. Иначе -- нет. Если после изменения n-ой (последней) координаты f(x[k]) <f(xB), то переход к п.4, иначе -- к п.7.
4. Полагают, что x[k] является новой базисной точкой xB, и вычиcляют значение f(xB).
5. Производят спуск из точки x[k]: xi[k+1] = 2Dxi[k] - xiB;i = 1, 2, …, n
где xiB -- координаты предыдущей базисной точки. Вычиcляют значение f(x[k+1]).
6. Как в п.3, циклически меняют каждую координату точки x[k+1] и сравнивают значения функции со значением из п.5. После изменения последней координаты сравнивают значения функции со значением f(xB) из п.5. Если неравенство выполняется, переход к п.4, иначе -- к п.3. При этом как базисную берут последнюю из полученных базисных точек.
7. Сравнивают Dx и e. Если Dx<e, вычисления прекращаются, иначе Dx уменьшают и переходят к п.3.
Недостаток метода: в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции можно не продвинуться к минимуму.
Например, для функций на Рис.8.4. Из точки x’ нельзя получить уменьшения целевой функции, каким бы малым не был шаг в направлении x1 и x2.
Метод деформируемого многогранника (метод Нелдера-Мида).
Идея метода:
в n-мерном пространстве строится многогранник, имющийn+1 вершину;
вычисляют значения функции в каждой вершине;
определяют максимальное значение функции и его вершину x[h];
через нее и центр тяжести остальных вершин проводится проецирующая прямая;
на ней находится точка x[q] c меньшим, чем в x[h], значением функции;
вершина x[h] исключается;
из оставшихся вершин и точки x[q] строится новый многогранник, после чего процедура повторяется.
В ходе описанной процедуры многогранник все время изменяет размеры (Рис.8.5.).
Рис. 8.5. Геометрическая интерпретация метода деформируемого многогранника
Обозначим
x[i, k] = (x1[i,k], …, xj[i,k], …, xn[i,k])T, -- i-ая вершина многогранника
на k-ом этапе поиска (i = 1, 2, …, n+1; k = 1, 2, …);
x[h, k] -- вершина, в которой значение целевой функции максимально;
x[l, k] -- вершина, в которой значение целевой функции минимально;
x[n+2, k] -- центр тяжести всех вершин, за исключением x[h, k].
Координаты центра тяжести
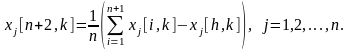
Алгоритм.
1. Проецируют точку x[h,k] через центр тяжести:
x[n+3,k] = x[n+2,k] + a (x[n+2,k] - x[h,k]),
где a -- некоторая константа (обычно а = 1).
2. Растягивают вектор x[n+3,k] - x[n+2,k]:
x[n+4,k] = x[n+2,k] + с (x[n+3,k] - x[n+2,k]),
где с > 1-- коэффициент растяжения (обычно 2,8 -- 3).
Если f(x[n+4,k]) < f(x[l, k]), то x[h,k] заменяют на x[n+4,k] и продолжают с п.1 приk = k + 1.
Иначе x[h,k] заменяют на x[n+3,k] и продолжают с п.1 приk = k + 1.
3. Если f(x[n+3,k])> f(x[i, k]) для всех i¹h, то сжимают вектор x[h,k] - x[n+2,k]:
x[n+5,k] = x[n+2,k] + b (x[h,k] - x[n+2,k]),
где b > 0 -- коэффициент сжатия (обычно 0,4 -- 0,6).
Затем точку x[h,k] заменяют на x[n+5,k] и продолжают с п.1 приk = k + 1.
4. Если f(x[n+3,k])> f(x[h, k]), то все векторы x[i,k] - x[l, k], I = 1, 2, … , n+1 уменьшают в два раза:
x[i,k] = x[l,k] + 0,5 (x[i,k] - x[l,k]).
Затем продолжают с п.1 приk = k + 1.
Выход из процесса происходит при предельном сжатии многогранника:
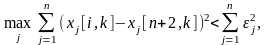
где e = (e1, …, en) – заданный вектор.
С помощью операции растяжения и сжатия размеры и форма многогранника адаптируются к топографии целевой функции. В результате многогранник вытягивается вдоль длинных наклонных плоскостей, изменяет направление в изогнутых впадинах, сжимается в окрестности минимума. Это определяет эффективность метода.
