5. Метод хорд.

Пусть корень с уравнения принадлежит отрезку [a, b], причем производные и 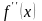непрерывны и сохраняют определенные знаки на данном отрезке. Сначала изучается расположение корней и осуществляется отделение корней. Затем выбирается начальное приближение x₀.

Правильный выбор начального приближения x₀ влияет на сходимость метода. При неправильном выборе x₀ каждое следующее приближение может все дальше удаляться от корня уравнения, т.е. метод хорд будет расходиться. Поэтому важным является следующее правило выбора начального приближения: неподвижен тот конец интервала [a,b], для которого знак функции f(x) совпадает со знаком ее второй производной , т. е. должно выполняться условие 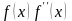>0.

Если 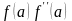>0, то точкаа является неподвижной, а в качестве начального приближения выбираем точку b, т. е. 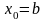и формула, определяющая алгоритм вычислений, имеет вид

. (3)

Если >0, то точка b является неподвижной, и в качестве начального приближения выбираем точку а, т. е. 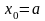и формула имеет вид

. (4)

Пример.

Методом хорд найти корни уравнения .

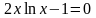Построив график функции 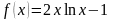, находим, что данное уравнение имеет один действительный корень, лежащий в интервале [1,4; 1,5].

Проверим условие нахождения корня в данном интервале 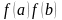< 0.

f(1,4) = - 0,05788 < 0,

f(1,5) = 0,21640 > 0.

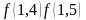<0, следовательно, условие нахождения корня в найденном интервале выполняется.

Далее найдем .

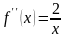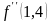= 1,42857 > 0,

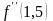= 1,33333 > 0.

Определим неподвижную точку согласно условию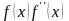 > 0. Так как > 0, то точка = 1,5 является неподвижной, а в качестве начального приближения корня выбираем точку = 1,4.

Каждое (n+ 1) приближение корня вычисляем по формуле .

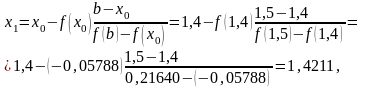
= 1,42152,

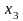= 1,42153,

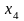= 1,42153.

Сравнивая и , видим, что корнем уравнения является число = 1,42153.

6. Метод Ньютона (метод касательных).

Основное достоинство метода – быстрая сходимость. Метод Ньютона универсален и пригоден для решения обширного класса уравнений.

Пусть корень с уравнения принадлежит отрезку [a, b], причем , и непрерывны и сохраняют определенные знаки на данном отрезке.

Если - некоторое приближение к корню с уравнения, то за новое приближение x₁ принимают точку пересечения касательной, проведенной в точке к графику функции f(x), с осью Ox.

Алгоритм поиска корня задает итерационная формула, позволяющая каждое последующее приближение к корню вычислить через предыдущее,

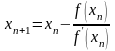, n = 0, 1, 2,... (2)

Если начальное приближение выбрано неудачно, то может случиться так, что следующее приближение x₁ к корню уравнения окажется вне интервала [a, b], что указывает на необходимость выбора другого начального приближения. В противном случае метод Ньютона может сходиться очень медленно, что приведет к накоплению погрешности вычисления, или не сходиться вообще.

Пример.

Методом Ньютона (касательных) вычислить корни уравнения .

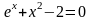Графически находим два интервала [-1,4; -1,3] и [0,5; 0,6].

Сразу найдем корень, принадлежащий [-1,4; -1,3].

f(-1,4) = 0,20660 > 0,

f(-1,3) = -0,03747 < 0.

< 0, следовательно, корень находится в этом интервале.

Корень будем уточнять по формуле .

За начальное приближение принимаем тот конец интервала [-1,4; -1,3], для которого выполняется условие > 0.

, .

= 2,27253 > 0, = 2,24660 > 0.

Для точки = -1,4 выполняется условие 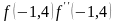> 0, поэтому положим = -1,4.

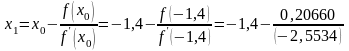= -1,31909,

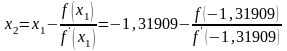= -1,31598,

= -1,31597,

= -1,31597.

Один корень уравнения = -1,31597.

Все в том же порядке повторим для интервала [0,5; 0,6].

f(0,5) = -0,10128 < 0,

f(0,6) = 0,18212 > 0.

< 0, следовательно, корень находится в этом интервале.

Для уточнения корня опять воспользуемся формулой .

За начальное приближение принимаем тот конец интервала [0,5; 0,6], для которого выполняется условие > 0.

Так как для точки = 0,6 выполняется условие 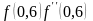> 0, то положим = 0,6.

Проделав выкладки, аналогичные предыдущим, получим = 0,53727.