27. Экстремумы функций. Классификация методов безусловной оптимизации.

Решение многих теоретических и практических задач сводится к отысканию экстремума скалярной функции f(x) n-мерного векторного аргумента x.

Под x будем понимать вектор-столбец: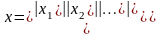

Вектор-строка получается путем транспонирования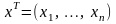

Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности.

В дальнейшем без ограничения общности будем говорить об отыскании минимума функции f(x)

f(x) ->min.

Вектор x*, доставляющий минимум целевой функции, называют оптимальным.

Задачу максимизации можно заменить эквивалентной задачей минимизации и наоборот.

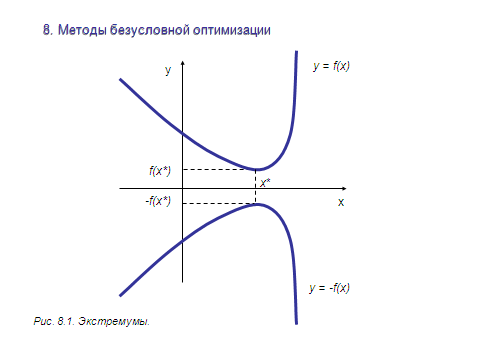
Рассмотрим это на примере функции одной переменной. Если x* -- точка минимума функции

y = f(x), то для функции y = -f(x) она – точка максимума.

Т.е. minf(x) = -max(-f(x)).

Сказанное справедливо и для функции многих переменных: minf(x1, …, xn) = -max(-f(x1, …, xn)).

Так что далее речь будет идти только о минимизации.

Точка x* доставляет глобальный минимум функции одной переменной f(x), заданной на числовой прямой X, если x* € X и f(x*) ≤ f(x) для всех x € X.

Точка x* называется точкой строгого глобального минимума, если неравенство выполняется как строгое.

Если же в выражении f(x*) ≤ f(x) равенство возможно при x ≠ x*, то реализуется нестрогий минимум, а под решением понимают множество x*={x € X : f(x) = f(x*)} .

Точка x* € X доставляет локальный минимум функции f(x) на множестве X, если при некотором, достаточно малом ε> 0 для всех x ≠ x*, x* €X, удовлетворяющих условию |x – x*| ≤ε, выполняется неравенство f(x*) ≤f(x).

Если неравенство строгое, x* является точкой строгого локального минимума.

Все определения для максимумов функции получаются заменой знаковв неравенствах на обратные.

На Рис.8.3. показаны экстремумы функции одной переменной f(x) на отрезке [a, b].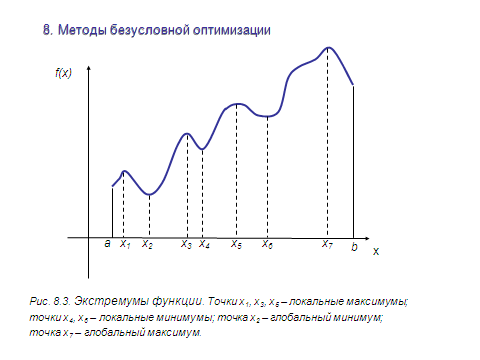

Классификация методов

Возможны два подхода для отыскания минимума функции многих переменных f(x) = f(x1, … , xn) при отсутствии ограничений на диапазон изменения неизвестных.

Первый подход лежит в основе косвенных методов оптимизации. Задача сводится к решению системы нелинейных уравнений.

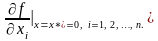В точке экстремума x* все первые производные функции по независимым переменным обращаются в ноль:

Эти условия образуют систему из n нелинейных уравнений. Вектор f’(x), составленный из первых производных по каждой переменной, называютградиентом скалярной функции f(x). В точке минимума градиент равен 0.

Решение системы нелинейных уравнений -- часто непростая задача. Поэтому на практике применялся иной подход. Он составляет основу прямых методов оптимизации.

Идея: построение последовательности векторов x[0], x[1], … x[n], …, таких что

f(x[0]) > f(x[1]) >…> f(x[n]) > …

Здесь [i] нумерует точки (и итерации).

Точку x[0] выбираем произвольно, но лучше недалеко от минимума.

Переход (итерация) от точки x[k] к точке x[k+1] (k = 0, 1, 2, ….) состоит из двух этапов:

1) выбор направления движения;

2) определение шага вдоль выбранного направления.

Методы построения таких последовательностей называют методами спуска -- переход от больших значений функции к меньшим.

Методы спуска описываются так:

x[k+1] = x[k] + ak p[k] , k = 0, 1, 2, …,

где p[k] -- вектор, определяющий направление спуска; ak -- длина шага.

В координатной форме:

Разные методы спуска - разные способы выбора параметров (направления и шага).

Метод должен сходиться - за конечное число шагов надо найти минимум или приблизиться.

Качество методов оценивают по скорости сходимости.

Критерии останова итераций либо малость приращения аргумента

или функции

Здесь k -- номер итерации; ε, γ -- заданные величины точности.

Метод поиска детерминирован, если оба параметра (направление и шаг) для перехода от x[k] к x[k+1] выбираются однозначно, по доступной в точке x[k] информации.

Если при переходе применяется механизм случайного выбора, алгоритм называется случайным поиском минимума.

Детерминированные алгоритмы делят на классы в зависисмости от вида используемой информации.

Если на каждой итерации используется

лишь значение функции - методы нулевого порядка;

если плюс к этому надо вычислять первые производные от минимизируемой функции - методы первого порядка;

если плюс к этому надо вычислять вторые производные от минимизируемой функции - методы второго порядка.

Характеристики качества метода:

скорость сходимости;

время выполнения одной итерации;

объем ОЗУ, нужный для решения задачи;

класс решаемых задач и др.

Задачи могут иметь малую или большую размерность, быть унимодальными или многоэкстремальными и т.д.

Как правило, имеющиеся методы не универсальны.

Выбор - исходя из специфики задачи.