11. Интерполяционная формула Лагранжа

Как для произвольно заданных узлов интерполирования, так и для равномерно отстоящих узлов применяется интерполяционная формула Лагранжа:

(3.6)

При n = 1 (линейная интерполяция) формула (3.6) представляет собой уравнение прямой y=L₁(x) , проходящей через две заданные точки (x₀,y₀), (x₁,y₁):

(3.7)

При n = 2 (квадратичная интерполяция) формула (3.6) представляет собой уравнение параболы y = L₂(x) , проходящей через три заданные точки (x₀,y₀), (x₁,y₁) и (x₂,y₂):

(3.8)

Разность называется погрешностью интерполяции или остаточным членом интерполяции.

В узлах интерполяции погрешность = 0, в остальных точках она отлична от нуля.

Если f(x) имеет непрерывную (n + 1) производную, то возможно представление остаточного члена интерполяции в виде (3.9)

где x зависит от x и лежит внутри отрезка [a,b] (a = x₀ < x₁< ... x_n= b).

Формула (3.9) справедлива для всех точек отрезка [a, b], в том числе и для узлов интерполирования.

Принимая , получим оценку погрешности интерполяции в текущей точке :

Оценка максимальной погрешности интерполяции на всем отрезке [a, b]:

Пример 1.

Построить интерполяционный полином Лагранжа для функции на , если С помощью интерполяционной формулы вычислить и оценить погрешность.

Имеем три узла интерполяции Так как n = 2 , то строим полином второй степени L₂(x).

Воспользуемся формулой (3.8). =

Погрешность интерполяции оценим, используя формулу (3.10):

Получим следующую оценку:

Используя полученный интерполяционный полином L₂(x), вычислим

= 0,264333

Таким образом, (Точное значение )

Пример 2.

Дана таблица значений y = f(x).

i	0	1	2	3
x	3,10	3,25	3,45	3,50
y	7,21	7,53	7,95	8,01

Найти значение f(3,30).

Чтобы найти значение в любой промежуточной точке необходимо построить

интерполяционный полином по табличным данным. Построим полином Лагранжа

для n = 3 (i = 0,1,…, n).

Итак, интерполяционный полином Лагранжа для заданных табличных данных имеет следующий вид

Для нахождения значения f(3,30) используем полученный полином Лагранжа, т. е.

12. Интерполирование сплайнами

На практике многие кривые нельзя описать простыми функциями.

Однако их можно составить из отрезков полиномов или других сравнительно

простых кривых.

В теории приближения функций такие кривые называются сплайнами.

На практике чаще всего применяются кубические сплайны.

Постановка задачи:

Пусть на отрезке [a, b] задана сетка a = x₀<x₁< …<x_n = b, в узлах которой заданы значения f(x_i) (i = 0, 1, 2,…, n) функции f(x) , определенной на [a, b].

Причем узлы сетки a = x₀<x₁< …<x_n = b не обязательно расположены равномерно.

Выберем, например, интервал между x_j и x_j+1. Цель интерполяции кубическими сплайнами – получить такую интерполяционную формулу, которая будет иметь гладкую первую производную и непрерывную вторую производную как внутри интервала, так и на его границах.

Рассмотрим задачу построения интерполяционного кубического сплайна, приближающего функцию f(x) , заданную на отрезке [a, b].

Кубическим сплайном, соответствующим данной функции f(x) и узлам , является функция S(x) , удовлетворяющая следующим условиям:

1. на каждом из отрезков [x_i, x_i+1] (i = 0, 1, 2,…, n) функция S(x) является многочленом третьей степени вида

i = 0, 1, 2,…, n-1;(3.26)

2. непрерывны на [a, b];

3. должно выполняться условие интерполяции, т. е. i = 0, 1, 2,…, n-1.(3.27)

Так как на каждом из n отрезков [x_i, x_i+1] между узлами сетки сплайн S(x) определяется четырьмя коэффициентами a, b, c, d, то для его полного построения необходимо найти 4n чисел.

Найдем первую, вторую и третью производные многочлена S_i(x) :

(3.28)

(3.29)

Для любой точки x = x_i из (3.26), (3.28), (3.29) получаем

Согласно условию интерполяции (3.27) будем иметь

, (3.30)

, i = 0, 1, 2,…, n-1

(3.31)

Введем шаг разбиения интервала [a, b] (шаг сетки): , ( ).

Тогда (3.31) запишем в виде

Так как , то (3.32)

Согласно условию б) (условие непрерывности) в каждом узле x_i левая и правая производные должны быть равны, т. е. не должно быть точек разрыва и должны выполняться условия

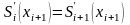(3.33)

(3.34)

Тогда , i = 0, 1, 2,…, n-2. (3.35)

Используя (3.34), получим

, i = 0, 1, 2,…, n-2. (3.36)

Полученные соотношения представляют собой алгебраическую систему для определения (4n-2) коэффициентов. Недостающие два уравнения получают из граничных условий. В общем случае рассматривают три вида граничных условий, которым должен удовлетворять сплайн S(x):

1) или ;

2) или ;

3)

Условия 1), 2) применяют, если известны значения соответствующих производных функции f(x) на концах отрезка [a, b]. Условия вида 3) называют периодическими и их выполнения требуют, если функция f(x) периодическая с периодом (b-a).

Для концевых узлов x₀, x_n полагаем (что соответствует нулевой кривизне графика на концах рассматриваемого отрезка). Тогда используя условия (3.11), получим

(3.37)

Заметим, что условие совпадает с (3.36) при i = n - 1, если положить c_n = 0.

Из (3.36) получим (3.38)

После подстановки a_i и d_i в (3.31) получим выражение для b_i:

(3.39)

Далее подставим b_i и d_i в (3.35) (и уменьшим значение индекса i на единицу для симметрии записи) и приходим к уравнениям:

(3.40)

Система (3.40) вместе с условиями c₀ = 0, c_n = 0, образует систему для определения

коэффициентов .

Другие коэффициенты сплайна вычисляются по формулам (3.30), (3.38) и (3.39).