36. Метод Ньютона с регулировкой шага (метод с переменной метрикой)

Употребляется также термин метод с переменной метрикой. Эти методы еще называют методами Ньютона ‑Рафсона, или демпфированными методами Ньютона. Они строятся по аналогии с градиентными методами с переменным шагом. Итерационный процесс в таком случае определяется выражением:

.

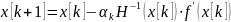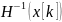– обратная матрица для матрицы Гессе; 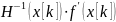– направление спуска.

Величина шага 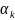выбирается из условия минимума функции f(x)поαв направлении движения, т.е. в результате решения задачи одномерной минимизации:

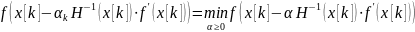
Вследствие накопления ошибок в процессе счета матрица Гессе на некоторой итерации может оказаться отрицательно определенной или ее нельзя будет обратить. В таких случаях в подпрограмме оптимизации полагают 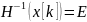, где E–единичная матрица. Очевидно, что итерация при этом осуществляется по методу наискорейшего спуска.

(Методы Ньютона требуют меньшей итерации, но по времени они могут быть намного больше.)

Он обладает сверх линейной или квадратичной скоростью сходимости в зависимости от требований.

В ряде случаев целесообразно комбинированное использование градиентных методов и метода Ньютона. В начале процесса оптимизации, когда точка x[0] находится далеко от точки экстремума x*, можно применять какой-либо вариант градиентных методов. Далее, при уменьшении скорости сходимости – метод Ньютона.

Алгоритм метода Ньютона

1. В начальной точке х[0] вычисляется вектор

р[0] = -H^-1(x[0])f'(x[0])

2. На k-й итерации определяются шаг a_k и точка х[k + 1] .

3. Вычисляется величина f(x[k + 1]).

4. Проверяются условия выхода, которые аналогичны условиям выхода изпри методе наискорейшего спуска. Если эти условия выполняются, вычисления прекращаются. Иначе -- вычисляется новое направление

p[k + 1] = -H^-1(x[k + 1])f’(x[k + 1])

и осуществляется переход к следующей итерации.

Количество вычислений на одной итерации методом Ньютона, как правило, гораздо больше, чем в градиентных методах.

Причина -- необходимость вычисления и обращения матрицы вторых производных целевой функции.

С другой стороны, на получение решения с достаточной точностью с помощью метода Ньютона обычно требуется намного меньше итераций, чем при использовании градиентных методов.

Поэтому метод Ньютона существенно более эффективен. Он обладает сверхлинейной или квадратичной скоростью сходимости в зависимости от требований, которым удовлетворяет минимизируемая функция f(x).

В некоторых задачах трудоемкость итерации методом Ньютона может перекрыть выигрыш от малого их числа.

37. Метод статистических испытаний (метод Монте-Карло)

Общая схема метода Монте-Карло:

Допустим, что нам требуется вычислить какую-то неизвестную величину m. Попытаемся придумать такую случайную величину ξ, чтобы Mξ=m. Пусть при этом Dξ=b².

Рассмотрим N случайных величинξ₁,ξ₂,…,ξ_N, распределения которых совпадают с распределениемξ.Если N достаточно велико, то согласно центральной предельной теореме теории вероятностей распределение суммы ρ_N=ξ₁+ξ₂+…+ξ_N будет приблизительно нормальным с параметрами a = Nm, σ²=Nb², из правила «трех сигм» следует, что

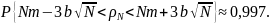
Если мы поделим неравенство, стоящее в фигурной скобке, на N, то получим эквивалентное неравенство и вероятность его останется такой же:

Последнее соотношение перепишем в несколько ином виде:

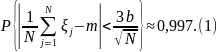
Это — чрезвычайно важное для метода Монте-Карло соотношение. Оно дает нам и метод расчета m, и оценку погрешности.

В самом деле, найдем N значений случайной величиныξ.Все равно, находить ли один раз по одному значению каждой из величин ξ₁,ξ₂,…,ξ_N или найти N значений одной величины ξ, так как все эти случайные величины совпадают (имеют одно и то же распределение). Из (1) видно, что среднее арифметическоеэтих значений будет приближенно равно m. С большой вероятностью ошибка такого приближения не превосходит величины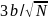 . Очевидно, эта ошибка стремится к нулю с ростом N.

При относительно небольшом числе испытаний в силу случайных причин меньшее число испытаний может иногда дать более точный результат, чем большее число испытаний.