22. Метод коллокации.

Решение краевой задачи (5.49),

(5.50) ищем в виде

где u_i(x) (I = 0, 1, 2, …, n) -- линейно независисмые ортогональные функции.

О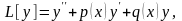 бозначим

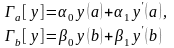
П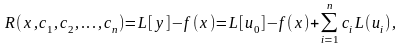 отребуем, чтобы невязка

обращалась в нуль на некоторой системе точек x1, x2, …, xn отрезка [a, b].

Эти точки называются точками коллокации, их число должно равняться числу коэффициентов c_i в выражении (5.60).

Для определения c_i получаем систему уравнений

Метод коллокации можно применить и для решения нелинейных уравнений

y’’ = f(x, y, y’).

c линейными краевыми условиями.

При этом невязка имеет вид

R(x) = y’’ - f(x, y, y’).

Система (5.63) будет системой нелинейных алгебраических уравнений относительно неизвестных ci.

Пример.

Методом коллокации найти приближенное решение уравнения

y’’ + (1 + x2)y + 1 =0

c краевыми условиями

y(-1) = y(1) = 0.

Выберем в качестве базисных функций u₀(x) = 0, u₁(x) = 1 – x₂, u₂(x) = x₂(1-x₂).

У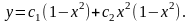 словия (5.65) для них выполняются. Решение будем искать в виде

З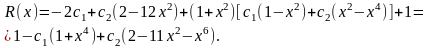 а точки коллокации возьмем x₀ = 0, x₁ = ½.Составляем невязку R(x):

П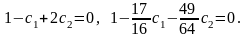 одставив x₀ = 0, x₁ = ½, получаем систему

Отсюда находим c1 = 0,957; c2 = -0,022.

Приближенное решение имеет вид

(взяла из интернета)

23.Аппроксимация производных конечно-разностными соотношениями.

«Идея метода заключается в сведении краевой задачи к решению системы алгебраических уравнений путем замены производных в дифференциальном уравнении и краевых условий конечно – разностными соотношениями»[3, 146 c.].

«Рассмотрим первую краевую задачу: { y" + p(x)y' + q(x)y = f(x), a < x < b; (3.1)

y(a) = ya, x = a; (3.2)

y(b) = yb, x = b (3.3)

и будем решать ее конечно - разностным методом, заменяя дифференциальные операторы отношением конечных разностей с использованием формул численного дифференцирования.

Для этого введем конечно-разностную сетку с шагом h: ω h = {xi = ih, i = 0,...,n}.

Поскольку ОДУ (3.1) описывает поведение функции у(х) внутри расчетной области x ∈ (a,b) , то производные 1-го и 2-го порядков можно аппроксимировать с помощью отношения центральных разностей со 2-м порядком аппроксимации: (3.4)

(3.5)

{p(xi), q(xi), f(xi)} ≡ {pi, qi, fi}, i= 1,...,n-1 (3.6)

Подставляя (3.4)-(3.6) в ОДУ (3.1), получим следующую конечно-разностную схему:

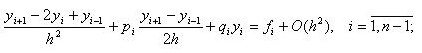
y0 = ya, i = 0; yn = yb, i = n, которую можно представить в виде следующей СЛАУ с трехдиагональной матрицей: a_i y_i-1 + b_iy_i + c_iy_i+1 = d_i, i=1,...,n-1, (3.7)

где di = fi.

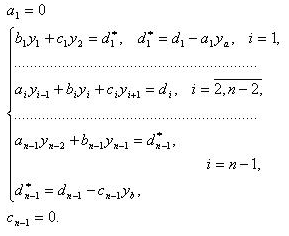П ри i = 1 первое слагаемое в левой части (3.7) известно и равно a1y0 = a1ya; при i = n-1 последнее слагаемое в левой части также известно и равно c_n-1yn = c_n-1yb. Поэтому СЛАУ (3.7) приобретает следующий вид:

(3.8)

Здесь коэффициенты a_i и c_n-1 полагаются равными нулю только после вычисления правых частей d₁* и d_n-1*.

Теперь СЛАУ (3.8) пригодна для использования метода прогонки (она имеет трехдиагональную матрицу и a₁ = c_n-1 = 0).