9. Приближенное решение систем нелинейных уравнений. Метод итерации.

Пусть дана система нелинейных уравнений

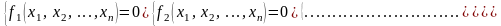(2.11)

или в матричной форме (2.12), где матрица F(X) имеет вид

Пусть система (2.11) приведена к виду: 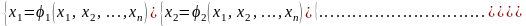(2.13)

или в матричной форме 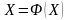(2.14), где матрица Ф(X) имеет вид

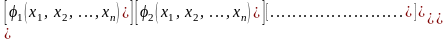
Каждое последующее (n+1) приближение можно вычислить по итерационной формуле

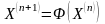, (n = 1, 2, …) (2.15)

Условие сходимости: процесс итерации (2.15) сходится к единственному решению системы (2.14), если выполняется одно из условий

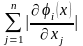£ q_i< 1, (i = 1, 2, …, n) или £ q_i< 1, (i = 1, 2, …, n)

Начальное приближение 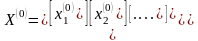выбирают произвольно из области сходимости метода итерации.

Процесс итерации может быть применен также к общей системе нелинейных уравнений (2.12). Перепишем эту систему в виде

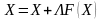(2.16), где L - неособенная матрица (ее определитель не равен нулю).

Сравнивая (2.14) и (2.16), видим, что

,

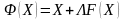Если F(X) имеет непрерывную производную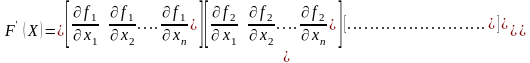

в некоторой окрестности изолированного решения системы (2.11), то, учитывая (2.17), получим

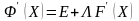
Учитывая условие сходимости процесса итерации, матрицу L выбираем таким образом, чтобы

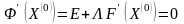
Отсюда, если матрица 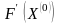неособенная, то будем иметь

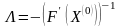
Учитывая сказанное, получим итерационную формулу для нахождения корней системы (2.1)

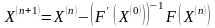
Замечание: в случае, если 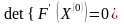, следует выбрать другое начальное приближение X⁽⁰⁾.

Пример:

Методом итерации решить систему нелинейных уравнений

В матричном виде заданная система уравнений имеет вид F(X) = 0, где

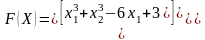
Итерационная формула, по которой можно найти корни данной нелинейной системы, имеет следующий вид

В качестве начального приближения возьмем матрицу

Тогда

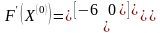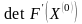, =36

Если определитель матрицы = 0 , то необходимо выбрать другое начальное приближение X⁽⁰⁾.

;

, , , , ,

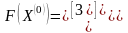
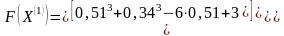
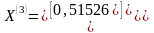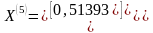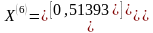Решением данной системы является матрица

10. Постановка задачи интерполирования функций. Общее решение задачи интерполирования функции полиномом.

Иногда нам известны значения функции f(x) лишь в наборе точек x₀, x₁, x₂…x_n (x₀<x₁< ... <x_n), но не известно аналитическое выражение для f(x). Часто, но не обязательно, точкиx являются равноотстоящими. В то же время необходимо найти значение функции в промежуточных точках. Порой при этом надо провести более или менее гладкую кривую через заданный набор точек, возможно даже и за пределами заданного набора.

Если надо найти значение функции для x₀<x₁< ... <x_n, то эта задача интерполяции, если x за пределами набора точек – задача экстраполяции.

Интерполяция связана с аппроксимацией функции, но отличается от нее.

Пусть в точках а = x₀< x₁< ... <x_n = b, называемых узлами интерполяции, функция задана таблицей своих значений

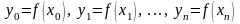(3.1)

Задача интерполирования заключается в том, чтобы построить функцию g(x)(интерполирующая функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x) , т. е. такую, что

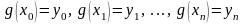
Геометрически это означает, что нужно провести кривую y = g(x) некоторого определенного типа, проходящую через систему заданных точек.

Линейную комбинацию

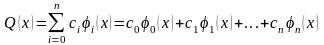(3.2)

с действительными коэффициентами c_i называют обобщенным многочленом (полиномом) по системе функций {j_i(x)} , i = 0, 1, …, n.

На практике чаще всего используются следующие системы:

1) 1, x, x², …, xⁿ, … -- алгебраическая интерполяция;

2) 1, sinx, cosx,…, sinnx, cosnx, … -- тригонометрическая интерполяция (применяется для приближения периодических функций);

3)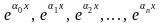 -- экспоненциальная интерполяция (где a_i - некоторая числовая последовательность попарно различных действительных чисел).

Любую функцию можно разложить по полиномиальному набору функции.

Рассмотрим интерполирование функции f(x) полиномом Q_n(x) степени не выше n, удовлетворяющим условию (3.2), т. е. таким, что

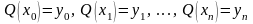(3.4)

Такой полином называется интерполяционным.

Как известно, существует единственный полином вида степени не выше n, принимающий в точках x₀ , x₁ , x₂ , … , x_n заданные значения.

Коэффициенты а_i полинома Q_n(x) можно определить из следующей системы уравнений:

(3.5) (где 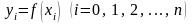) (комет.:x и yизвестны, а подлежат определению). Определителем этой системы является определитель Вандермонда

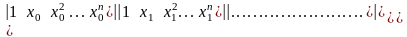¹ 0.Он отличен от нуля при всяких различных между собой x_i, следовательно, интерполяционный многочлен существует и он единственный.