2. Аксіоми раціональної поведінки
У [1] вводиться п’ять аксіом раціональної поведінки і доводиться існування функції корисності. Розглянемо ці аксіоми на змістовному рівні. Позначимо через x, y, z різні результати процесу вибору, а через p, q ймовірності тих чи інших результатів. Уведемо визначення лотереї. Лотереєю називається гра з двома результатами: результатом x, який має ймовірність p, і результатом y, який має ймовірність q.
x
p
1–p y
Рис.2. Представлення лотереї
Прикладом лотереї є підкидання монети. При цьому, як відомо, з імовірністю p=0,5 випадає герб або число. Нехай x=10 грн і y=–10 грн (тобто ми одержуємо 10 грн під час випадіння герба і платимо стільки ж, якщо випаде число). Очікувана (або середня) ціна лотереї визначається за формулою px+(1–p)y. Наведемо аксіоми раціонального вибору.
Аксіома 1. Результати x,y,z належать множині A результатів випробувань.
Нехай P означає відношення строгої переваги (схоже на відношення > в математиці); R – відношення нестрогої переваги (схоже на відношення ); I – байдужість (схоже на відношення рівності =). Ясно, що R включає P i I.
Аксіома 2. Для відношення R виконуються умови:
1) зв’язності: або xRy, або yRx, або перше і друге разом;
2) транзитивності: із xRy i yRz випливає xRz.
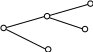
Аксіома 3. Дві зображені на рис.3 лотереї знаходяться у відношенні байдужості.
Справедливість цієї аксіоми очевидна. Вона записується у стандартному вигляді як ((x,p,y)q,y) I (x, pq, y).
x
p pq
q
1–p
1–pq y
1–q
Рис.3. Дві лотереї, які знаходяться у відношенні байдужості
Аксіома 4. Якщо xIy, то (x,p,z)I(y,p,z).
Аксіома 5. Якщо xPy, то xP(x,p,y)Py.
Аксіома 6. Якщо xPyPz, то існує ймовірність p, така, що yI(x,p,z).
Усі наведені вище аксіоми достатньо прості для розуміння і здаються очевидними.
За умови їх виконання буда доведена наступна теорема: якщо аксіоми 1–6 виконуються, то існує числова функція U, визначена на множині A (множині результатів), і така, що:
1) xRy тоді і тільки тоді, коли U(x) U(y);
2) U(x,p,y)=pU(x)+(1–p)U(y).
Функція U(x) вимірюється в шкалі інтервалів (див. лекцію 1). Функція U(x) – єдина з точністю до лінійного перетворення (наприклад, якщо Ux) U(y), то aU(x) aU(y), де A – ціле додатнє число.
3. Задача з вазами
Теорія корисності експериментально досліджувалась у так званих задачах про вази (або урни). Ваза – це непрозора посудина, в якій знаходиться певна (відома лише організаторові експерименту) кількість кульок різного кольору. Задачі з вазами типові для групи найбільш простих задач прийняття рішень – задач статистичного типу. Для розв’язування задач цього типу необхідно знати елементарні теореми теорії ймовірностей [2]. Людина робить вибір у цих задачах, спираючись на розрахунки. Варіанти дій виражені в найпростішій формі.
Типова задача статистичного типу формулюється таким чином. Перед ОПР ставиться ваза, яка може бути вазою 1–го або 2–го типу. ОПР повідомляється: скільки є в наявності ваз 1–го і 2–го типів; скільки червоних і білих кульок знаходиться у вазах цих типів; які виграші очікують ОПР, якщо вона вгадає, якого типу ваза; які програші чекають її, якщо вона помилиться. Після одержання такої інформації ОПР повинна зробити вибір: назвати, до якого типу належить поставлена перед нею ваза, d1 – ваза 1-го типу, d2 – ваза 2-го типу.
Нехай, наприклад, експериментатор випадково вибирає вазу із множини, яка містить 700 ваз 1–го типу і 300 ваз 2–го типу. У вазі 1–го типу знаходиться 6 червоних і 4 білі кулі. У вазі 2–го типу міститься 3 червоні і 7 білих куль. Якщо перед ОПР знаходиться ваза 1–го типу і вона це вгадає, то отримає виграш 350 грн, якщо не вгадає, її програш складе 50 грн. Якщо перед нею ваза 2–го типу і ОПР це вгадає, то одержить виграш 500 грн, якщо не вгадає, її програш складе 100 грн. ОПР може здійснити одну з таких дій:
Таблиця 2.2
Представлення задачі з вазами
-
Типи
вази
Ймовірність вибору вази даного типу
Виграш при дії
d1
d2
1
0,7
350
–100
2
0,3
–50
500
Яке ж рішення необхідно прийняти? Теорія корисності пропонує: оцінити середню (очікувану) корисність кожної з дій і вибрати дію з максимальною очікуваною корисністю. Відповідно до цієї рекомендації ми можемо визначити середнє значення виграшу для кожної дії:
U(d1) = 0,7 350 – 0,3 50 = 230 грн;
U(d2) = 0,3 500 – 0,7 100 = 80 грн.
Отже, раціональна людина вибере дію d1 , а не дію d2.
Із цього прикладу випливає загальний принцип поведінки раціональної людини: визначити можливі результати дій, помножити їх на відповідні ймовірності, одержати очікувану корисність і вибрати дію з найбільшою корисністю.
Задачі з вазами допоможуть нам ознайомитись із побудовою дерева розв’язків і прийняттям рішень за їх допомогою.