2. Індивідуальний вибір

Розглянемо індивідуальний вибір рішень для задач з однією ціллю і декількома альтернативами, тобто задачу типу IS. Постановка задачі вибору формулюється таким чином. Нехай маємо декілька альтернативних ситуацій S=(S₁, S₂, …, S_n), для яких відомі ймовірності їх появи p=(p₁, p₂, …, p_n) і множина допустимих рішень Y_д=(Y₁, Y₂, …,Y_m). Проведено вимірювання функції переваг на множині альтернатив, тобто визначені значення функції переваг .

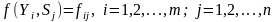Наявність альтернативних ситуацій породжує невизначеність вибору оптимального рішення. Для усунення цієї невизначеності можна використати два способи.

Перший із них полягає в тому, що для кожної окремо взятої альтернативи визначається своє оптимальне рішення. Застосування конкретного рішення пов’язане з появою конкретної ситуації. Очевидно, цей спосіб можливий тільки тоді, коли можна чекати появи конкретної ситуації. Характерним прикладом такого підходу є інструкція на випадок пожежі.

Другий спосіб усунення невизначеності застосовується тоді, коли рішення повинно бути прийняте до одержання інформації про те, яка з альтернатив у дійсності має місце. Суть цього способу полягає в урахуванні впливу всіх альтернатив на вибір оптимального рішення. Можливі різні способи врахування цього впливу, які розрізняються між собою характером прийнятої стратегії дії ОПР і вибором конкретного критерію оптимальності.

Розрізняють три види стратегій: обережна (песимістична), оптимістична і раціональна (розрахована на середні умови).

Обережна стратегія спирається на принцип "розраховуй на гірше". Відповідно оптимістична – на принцип "розраховуй на краще". У випадку раціональної стратегії ОПР розраховує на найбільш імовірні умови. Вибір тієї чи іншої стратегії здійснює ОПР на основі характеру розв’язуваної проблеми, сформульованих цілей та індивідуальних особливостей свого мислення.

Кожному виду стратегії можна поставити у відповідність сукупність критеріїв вибору оптимального рішення. Критерій вибору однозначно визначає правило вибору оптимального рішення. Слід відзначити, що однозначність правила вибору не гарантує одержання єдиного оптимального рішення, їх може виявитись декілька.

У якій відповідності знаходяться критерій вибору оптимального рішення і ціль розв’язування проблеми? Одну і ту ж ціль можна досягти, діючи обережно, ризиковано чи раціонально. Тоді залежно від проблемної ситуації можна отримати різний ступінь досягнення цілі. Ціль визначає бажаний кінцевий результат або стан. Стратегія вибору – це характер поведінки ОПР із метою досягнення цілі. Критерій вибору – це конкретизація характеру дій, поведінки ОПР для досягнення цілі. Нарешті, оптимальне рішення – це сама дія досягнення цілі. Таким чином, для досягнення однієї і тієї ж цілі залежно від вибору стратегії і конкретного критерію може бути визначене різне оптимальне рішення.

Розглянемо типові критерії вибору оптимального рішення для трьох видів стратегії поведінки. Поставимо у відповідність кожному рішенню Y_i числовий коефіцієнт важливості рішення 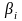. Залежно від виду критерію зміст коефіцієнтів важливості рішення буде різним, але загальне правило вибору оптимального рішення можна записати в одному і тому ж вигляді

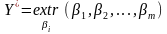. (4.1)

Цей запис означає, що необхідно з множини чисел вибрати екстремальне число (операція extr) і за номером цього числа визначити, яке з альтернативних рішень є оптимальним.

Якщо коефіцієнти важливості рішень визначені так, що більшому числу відповідає краще рішення, то операція знаходження екстремуму відповідає операції знаходження максимуму, тобто в цьому випадку співвідношення (4.1) має вигляд

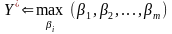. (4.2)

Цей запис означає, що із сукупності чисел знаходиться найбільше число (операція знаходження max) і відповідно до номера цього числа визначається оптимальне рішення.

Якщо коефіцієнти важливості рішень визначені так, що більшому числу відповідає гірше рішення, то операція знаходження екстремуму відповідає операції знаходження мінімуму, тобто в цьому випадку співвідношення (4.1) має вигляд

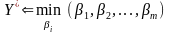. (4.3)

Відповідно до цих записів із множини чисел знаходиться найменше чи найбільше число, за яким і визначається оптимальне рішення.

2.1. Критерій песимізму є типовим представником сукупності критеріїв, які відповідають обережній стратегії поведінки. Застосування цього критерію не вимагає знання ймовірностей альтернатив, і в цьому його перевага, так як часто ці ймовірності не відомі.

Для того, щоб використати загальне правило вибору оптимального рішення для частинного випадку критерію песимізму, необхідно визначити коефіцієнти важливості рішень. Для кожної k-ої цілі маємо оцінку переваги цього рішення для будь-якої j-ої альтернативи. Оскільки критерій песимізму відповідає правилу "розраховуй на гірший випадок", то в ролі коефіцієнта важливості i-го рішення слід вибрати найгірше значення функції переваг з усіх ситуацій. Якщо функція переваг вимірюється так, що її найкращому значенню відповідає найбільше число, то очевидно, що найгірше значення функції переваг є її найменшим значенням. Тому обчислення коефіцієнта важливості рішень проводиться за формулою

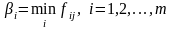. (4.4)

Це означає, що для i-го рішення вибирається з усіх j-х альтернатив найменше значення функції переваг.

Використовуючи загальне правило рішення (4.2) і співвідношення (4.4), правило знаходження оптимального рішення за критерієм песимізму можна записати у вигляді

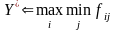. (4.5)

Відповідно до цього правила послідовно виконуються операції знаходження максимального значення функції переваг для всіх альтернатив, а потім із одержаних чисел знаходиться максимальне число, номер якого і визначає оптимальне рішення. Критерій песимізму, виходячи з правила (4.5), називають максмінним критерієм.

Якщо вимірювання функції переваг здійснюється в порядковій шкалі, найгірше з усіх альтернатив рішення відповідає максимальному значенню функції переваг. Отже, коефіцієнт важливості під час вимірювання переваг у рангах обчислюється за формулою

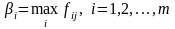. (4.6)

Відповідно правило вибору оптимального рішення за критерієм песимізму при вимірюванні переваг у порядковій шкалі має вигляд

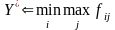, (4.7)

де f_ij – ранг i-го рішення для j-ї альтернативи. Зміст операцій у співвідношенні (4.7) полягає в тому, що переглядаються ранги рішень для всіх альтернатив і визначається найбільший ранг, тобто найгірша оцінка рішення (операція max f_ij). Далі з усіх одержаних чисел вибирається найменше, тобто найвищий ранг. Номер коефіцієнта важливості , який має найвищий ранг, указує на оптимальне рішення.

2.2. Критерій оптимізму відповідає оптимістичній стратегії вибору. Відповідно до принципу "розраховуй на кращий випадок" коефіцієнти важливості рішень визначаються як найкращі оцінки переваг для всіх альтернатив. Якщо вимірювання проводяться в кількісних шкалах таким чином, що її найкращому значенню відповідає найбільше число, то коефіцієнти важливості рішень визначаються таким чином:

, (4.8)

де f_ij – значення функції переваг, які виміряні в кількісній шкалі і які відображають корисність i-го рішення для j-ї альтернативи. Відповідно до загального правила вибору рішень (4.2) правило вибору рішення, яке відповідає критерію оптимізму, має вигляд

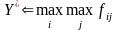. (4.9)

Якщо вимірювання переваг проводиться в порядковій шкалі і f_ij є ранг i-го рішення для j-ї альтернативи, то коефіцієнти важливості рішень обчислюються шляхом застосування операції мінімуму до множини рангів оцінки рішення для всіх альтернатив:

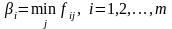. (4.10)

Правило вибору рішення у випадку вимірювання переваг у рангах і критерію оптимізму має вигляд:

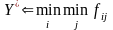. (4.11)

Як випливає з правила вибору оптимального рішення за критерієм оптимізму, в ролі початкової інформації використовується тільки значення функції переваг, тобто оцінки рішень по досягненню цілі для різних альтернатив. Значення ймовірностей альтернатив під час використання цього критерію так же, як і для критерію песимізму, не потрібні. Це є позитивною властивістю даного критерію вибору.

2.3. Критерій максимуму середнього виграшу є представником групи критеріїв, які відповідають раціональній стратегії. Загальне правило вибору рішення (4.1) або (4.2) залишається справедливим і в цьому випадку. Конкретизація виду правила вибору рішення вимагає визначення коефіцієнта важливості рішення. В даному випадку коефіцієнти важливості рішень являють собою середній виграш, який одержується для кожного рішення за всіма альтернативами.

Якщо переваги рішень на множині альтернатив вимірюються в інтервальній шкалі (або шкалі відношень), то середній виграш обчислюється як математичне сподівання виграшу:

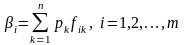, (4.12)

де p_k – імовірність k-ї альтернативи, f_ik – значення функції переваг, яка оцінює i-е рішення для k-ї альтернативи.

Розглянемо частинні випадки. Нехай вірогідність появи всіх альтернатив однакова (всі ймовірності рівні між собою). Оскільки сума ймовірностей усіх альтернатив дорівнює одиниці, то для рівних імовірностей одержуємо, що всі вони рівні 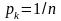, де n – кількість альтернатив. У цьому випадку середні виграші рішень обчислюються за формулою

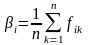. (4.13)

Множник 1/n не впливає на визначення максимуму, тому середні виграші рішень можна обчислити за формулою

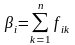. (4.14)

Якщо має місце тільки одна альтернатива, наприклад S_j , то її поява є достовірною подією і, отже, p_j=1. Решта альтернатив мають нульові ймовірності появи: p_k=0, j  k. У цьому випадку середні виграші просто дорівнюють значенням функції переваг для j-ї альтернативи

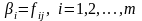. (4.15)

Розглянемо тепер вимірювання функції переваг у порядковій шкалі, яке здійснюється методами ранжування або парного порівняння. У випадку ранжування завжди можна його результати представити у вигляді матриці парних порівнянь з елементами:

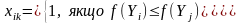
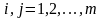, (4.16)

де f(Y_i) – ранг i-го рішення. Тому надалі критерій максимуму середнього виграшу будемо розглядати для випадку вимірювання переваг рішень методом парних порівнянь.

Для кожної k-ї альтернативи результати оцінки переваг являють собою матрицю парних порівнянь з елементами 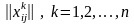. Сукупність матриць парних порівнянь можна розглядати як точки в просторі ранжування рішень. У цьому просторі можна ввести поняття відстані між точками – матрицями парних порівнянь – як число неспівпадань значень елементів матриць. Відстань між двома матрицями парних порівнянь обчислюється за формулою

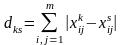, (4.17)

де d_ks – відстань між матрицями парних порівнянь рішень, одержаних для k-ї і s-ї альтернатив, 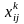– ij-й елемент матриці для k-ї альтернативи.

Для побудови середньої матриці парних порівнянь 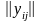використаємо умову мінімуму сумарної відстані цієї матриці від матриці парних порівнянь для всіх альтернатив:

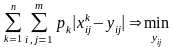, (4.18)

де p_k – імовірності альтернатив. Обчислимо операцію вибору мінімуму шляхом вибору елементів y_ij шуканої середньої матриці. Враховуючи те, що величини можуть приймати значення тільки нуль і одиниця, представимо модуль різниці як квадрат різниці

. (4.19)

Піднесемо вираз у круглих дужках до квадрата і приймемо до уваги, що

.

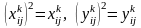У результаті одержимо

.

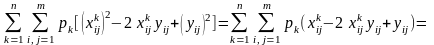
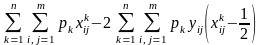Для заданих матриць парних порівнянь перший член у цьому виразі є постійна величина. Тому максимальне значення суми відстаней відповідає максимальному значенню другого члена, тобто умові (4.18) відповідає умова

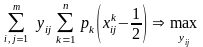. (4.20)

Максимальне значення суми досягається вибором значення y_ij за таким правилом:

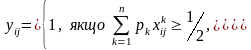(4.21)

Вибрані за правилом (4.21) елементи середньої матриці забезпечують мінімальну віддаленість у просторі ранжування цієї матриці від матриць парних порівнянь переваг рішень для всіх альтернатив з урахуванням імовірностей цих альтернатив.

Обчислення коефіцієнтів середнього виграшу рішень проводиться з використанням елементів y_ij за формулою

, i=1,2,…,m. (4.22)

Одержані значення коефіцієнтів рішень для критерію максимуму середнього виграшу дозволяють використовувати загальне правило вибору (4.5) для визначення оптимального рішення.

2.4. Критерій песимізму-оптимізму (критерій Гурвіца) також є різновидом раціональної стратегії вибору рішень. Застосування цього критерію не вимагає знання ймовірностей альтернатив. Даний критерій являє собою зважену комбінацію критеріїв песимізму й оптимізму. Правило вибору оптимального рішення за критерієм песимізму-оптимізму має вигляд

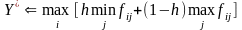, (4.23)

де f_ij – значення функції переваг під час оцінки i-го рішення для k-ї альтернативи, виміряні в кількісній шкалі так, що більшій перевазі відповідає більше значення числа; h – коефіцієнт ваги песимізму, який змінюється в діапазоні 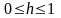. При h=0 критерій песимізму-оптимізму перетворюється в критерій оптимізму. При h=1 відповідно маємо критерій песимізму. Вибір значення коефіцієнта ваги песимізму здійснює ОПР відповідно до своїх уявлень про долю оптимізму і песимізму під час вибору рішення.

Зауважимо, що вираз у квадратних дужках (4.23) – це коефіцієнти рішень у випадку песимізму-оптимізму:

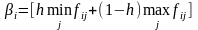. (4.24)

Якщо переваги вимірюються у порядковій шкалі і величини f_ij є ранги, то використання критерію песимізму-оптимізму полягає в наступному. Визначаються коефіцієнти важливості рішень для критерію песимізму відповідно до формули (4.6) і за ними проводиться ранжування рішень. У результаті маємо два ранжування рішень: одне – за критерієм песимізму, друге – за критерієм оптимізму. Ці ранжування перетворюються в матриці парних порівнянь за правилом (4.16). Матриця парних порівнянь, яка відповідає критерію песимізму, множиться на коефіцієнт h , а матриця парних порівнянь для критерію оптимізму – на коефіцієнт 1-h . Одержані в результаті множення матриці додаються. Далі в одержаній матриці елементи замінюються на нуль або одиницю за правилом

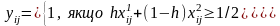, (4.25)

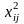де – елементи матриці парних порівнянь рішень для критерію песимізму, – елементи матриці парних порівнянь рішень для критерію оптимізму.

Коефіцієнти важливості рішень для критерію Гурвіца обчислюються з використанням елементів y_ij за формулою

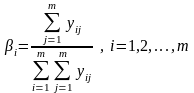. (4.26)

Оптимальне рішення для критерію Гурвіца визначається шляхом знаходження максимального значення коефіцієнта важливості. Номер цього коефіцієнта відповідає номеру оптимального рішення.

В ряді випадків ОПР утруднюється обгрунтовано вибрати критерій одержання оптимального рішення. В таких випадках доцільно провести аналіз різних критеріїв. Для цього необхідно знайти оптимальні рішення за допомогою різних критеріїв, визначити, збігаються чи відрізняються між собою одержані рішення, і оцінити вплив критеріїв на вибір оптимального рішення. Такий аналіз дозволяє ОПР більш осмислено і логічно вибрати критерій та відповідне йому оптимальне рішення.

Приклад 1. Визначимо оптимальне за критерієм песимізму рішення за результатами оцінки переваг у рангах, яка здійснена ОПР. Результати ранжування трьох рішень для трьох ситуацій S₁, S₂, S₃ наведені в таблиці 4.1.

Таблиця 4.1

	S1	S2	S3
Y1	1	2	1	2
Y2	2	1	3	3
Y3	3	3	2	3

Обчислимо значення коефіцієнтів рішень за формулою (4.10) 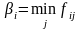, де 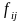– ранги, наведені в таблиці 4.1. Для першого рішення (i=1) найгірший ранг з усіх ситуацій дорівнює 2 і відповідає другій ситуації, тому 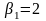. Для другого рішення 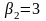і для третього 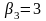. Таким чином, вектор коефіцієнтів рішень дорівнює .

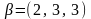Далі відповідно до формули (4.11) необхідно обчислити 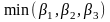. Мінімальне значення із трьох чисел (2,3,3) дорівнює 2, тому 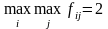. Значення 2 відповідає першому рішенню (перша компонента вектора 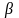), отже, за критерієм песимізму оптимальне рішення .

Приклад 2. Визначимо оптимальне за критерієм оптимізму рішення для випадку оцінки переваг у рангах для трьох ситуацій і трьох альтернативних варіантів рішення, для яких оцінки переваг задані в табл. 4.1. Обчислимо коефіцієнти рішень, використовуючи співвідношення (4.8). Для першого рішення найменше значення функції переваг дорівнює 1 (див. перший рядок табл. 4.1), отже, 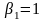. Для другого рішення найменше значення функції переваг для всіх ситуацій також дорівнює 1, тому 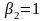. Нарешті, для третього рішення 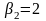. Знаходимо оптимальне рішення за формулою (4.9). Із трьох чисел , найменшими є два числа і . Отже, за критерієм оптимізму оптимальними є два рішення . 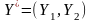Відмітимо, що рішення 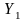виявилось оптимальним як за критерієм оптимізму, так і за критерієм песимізму.

Приклад 3. Визначити оптимальне за критерієм середнього виграшу рішення 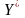із множини трьох допустимих рішень 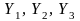для випадку чотирьох сит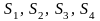уацій . ОПР визначила переваги для кожної ситуації у кількісній шкалі, які наведені в таблиці 4.2. В нижньому рядку цієї таблиці задані ймовірності ситуацій .

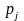Таблиця 4.2

	S1	S2	S3	S4
Y1	1	4	5	9	5.2
Y2	3	8	4	3	4.5
Y3	4	6	6	2	5.0
Pj	0.1	0.2	0.5	0.2

За формулою (4.12) обчислимо коефіцієнти рішень , які запишемо в останній стовпчик табл.4.2. Відповідно до правила (4.2) оптимальне рішення відповідає максимальному значенню коефіцієнта рішення. Очевидно, максимальним є коефіцієнт 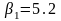, тому оптимальним є рішення .

Для цієї ж задачі знайдемо оптимальне за критерієм песимізму-оптимізму рішення з 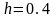. Значення цього коефіцієнта ваги оптимізму означає, що ОПР на 40 % вважає свою стратегію песимістичною і на 60 % оптимістичною. Виконуючи обчислення за формулою (4.24), одержимо значення коефіцієнтів рішень 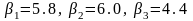. Звідси випливає, що оптимальним рішенням є .

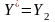Зауважимо, що після вибору меншого значення коефіцієнта песимізму, наприклад, , одержимо . Тому оптимальним буде рішення .

Приклад 4. Визначити оптимальне за критерієм середнього виграшу рішення з множини трьох допустимих рішень для трьох ситуацій S₁, S₂, S₃ , ймовірності появи яких відомі. ОПР визначила переваги рішень для кожної ситуації в порядковій шкалі. В табл.4.3 наведені значення функції переваг у рангах і ймовірності ситуацій.

Таблиця 4.3

	S1	S2	S3
Y1	1	2	1
Y2	2	1	3
Y3	3	3	2
Pj	0.5	0.3	0.2

Для кожної ситуації S_j запишемо переваги рішень у вигляді матриці парних порівнянь, керуючись правилом (4.16) і таблицею переваг 4.3. В таблицях 4.4, 4.5, 4.6 представлені матриці парних порівнянь, які відповідають ранжуванням табл.4.3 для ситуацій S₁, S₂, S₃ .

Таблиця 4.4 Таблиця 4.5

	Y1	Y2	Y3			Y1	Y2	Y3
Y1	1	1	1		Y1	1	0	1
Y2	0	1	1		Y2	1	1	1
Y3	0	0	1		Y3	0	0	1

Таблиця 4.6 Таблиця 4.7

	Y1	Y2	Y3			Y1	Y2	Y3
Y1	1	1	1		Y1	1	0,7	1
Y2	0	1	0		Y2	0,3	1	0,7
Y3	0	1	1		Y3	0	0,3	1

Обчислимо коефіцієнти рішень за формулами (4.21), (4.22). У формулі (4.21) сума 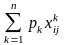означає, що треба помножити всі значення переваг у таблиці 4.4 на 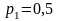; усі значення переваг у таблиці 4.5 на 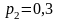; всі значення переваг у таблиці 4.6 на 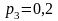і скласти одержані добутки. В результаті одержимо таблицю 4.7.

Далі, керуючись правилом (4.21), перетворимо елементи матриці 4.7. Замість 0,7 поставимо одиниці, замість 0,3 – нулі. В результаті одержимо матрицю 4.8 , в четвертому стовпчику якої запишемо коефіцієнти рішень , обчислені за формулою (4.22).

Таблиця 4.8

	Y1	Y2	Y3
Y1	1	1	1	0,5
Y2	0	1	1	0,333
Y3	0	0	1	0,167

Максимальне значення має коефіцієнт 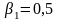, отже, оптимальним є рішення .

Зауважимо, що початкові дані цього прикладу відповідають даним прикладів 1 і 2. За всіма критеріями - песимізму, оптимізму і максимуму середнього виграшу – оптимальним є рішення .