Лекція 7. Групова оцінка об’єктів експертами

Розглянемо рішення задачі побудови узагальненої групової оцінки об’єктів шляхом обробки індивідуальних оцінок експертів. Відповідно до гіпотези, що експерти є досить точними "вимірювачами", групова оцінка будується на основі застосування методів усереднення. Це відповідає тому, що індивідуальні оцінки експертів утворюють компактну групу і в ролі найбільш узгодженої групової оцінки використовується математичне сподівання (середнє значення) або медіана (найбільш імовірна оцінка).

Нехай d експертів провели оцінку m об’єктів за l показниками. Результати оцінки представлені у вигляді величин , де s – номер експерта, i – номер об’єкта, h – номер показника (ознаки) порівняння. Якщо оцінка об’єктів проведена методом ранжування, то величини являють собою ранги. Якщо оцінка об’єктів виконана методом безпосередньої оцінки чи методом послідовного порівняння, то величини являють собою числа або бали. Обробка результатів оцінки істотно залежить від розглянутих методів вимірювання.

Розглянемо спочатку випадок, коли величини (s=1,2,…,d; i=1,2,…,m; h=1,2,…,l) одержані методом безпосередньої оцінки чи методом послідовного порівняння і, отже, є числами або балами. Для одержання групової оцінки об’єктів у цьому випадку можна скористатись середнім значенням оцінки для кожного об’єкта

, (7.1)

де q_h – вагові коефіцієнти показників порівняння об’єктів, k_s – коефіцієнти компетентності експертів. Вагові коефіцієнти показників та коефіцієнти компетентності експертів є нормованими величинами:

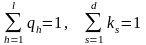. (7.2)

Вагові коефіцієнти показників можуть бути визначені експертним шляхом. Якщо q_hs – ваговий коефіцієнт h-го показника, який присвоєний s-м експертом, то середній ваговий коефіцієнт h-го показника для всіх експертів дорівнює

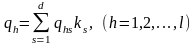. (7.3)

Одержання групової експертної оцінки шляхом підсумовування індивідуальних оцінок із ваговими коефіцієнтами компетентності і важливості показників під час вимірювання властивостей об’єктів у кількісних шкалах спирається на припущення про виконання аксіом теорії корисності Неймана-Моргенштерна як для індивідуальної, так і для групової оцінки. В реальних задачах ці умови, як правило, виконуються, тому одержання групових оцінок об’єктів шляхом підсумовування з ваговими коефіцієнтами індивідуальних оцінок експертів широко застосовується на практиці.

Коефіцієнт компетентності експертів можна обчислити за результатами оцінки об’єктів. Основна ідея цього обчислення полягає в припущенні, що компетентність експертів повинна оцінюватись за ступенем узгодженості їх оцінок із груповою оцінкою об’єктів.

Алгоритм обчислення коефіцієнтів компетентності експертів має вигляд рекурентної процедури:

, (7.4)

, (7.5)

. (7.6)

Обчислення починаються з 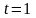. У формулі (7.5) початкові значення коефіцієнтів компетентності приймаються однаковими і рівними . Тоді за цією формулою групові оцінки об’єктів першого наближення дорівнюють середнім арифметичним значенням оцінок експертів

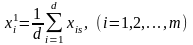. (7.7)

Далі обчислюється величина за формулою (7.5)

(7.8)

і значення коефіцієнтів компетентності першого наближення за формулою (7.6)

. (7.9)

Використовуючи коефіцієнти компетентності першого наближення, можна повторити весь процес обчислень за формулами (7.4) - (7.6) і одержати інші наближення величин 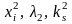і т. д.

Розглянемо тепер випадок, коли експерти проводять вимірювання в порядковій шкалі методом ранжування, так що величини 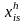(i – номер об’єкта, s – номер експерта, h – номер показника порівняння) – це ранги. Задача обробки полягає в побудові узагальненого ранжування на основі індивідуальних ранжувань експертів. Для спрощення розглянемо спочатку випадок однієї ознаки порівняння, тому індекс 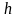у величинах опустимо. Кожне ранжування можна представити у вигляді матриці парних порівнянь з елементами, які визначаються за правилом

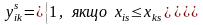, (7.10)

де 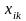і – ранги, які присвоюються s-експертом i-му і k-ому об’єктам. Нехай, наприклад, дано ранжування одним експертом (s=1)

.

Тоді матриця парних порівнянь для цього ранжування має вигляд (табл.7.1)

Таблиця 7.1

	О1	О2	О3	О4	О5
О1	1	1	1	1	1
О2	0	1	1	1	1
О3	0	0	1	1	1
О4	0	0	0	1	1
О5	0	0	0	0	1

Якщо маємо d експертів, то кожен експерт дає своє ранжування, якому відповідає матриця парних порівнянь. Таким чином, кількість матриць порівнянь дорівнює числу експертів.

Уведемо відстань (метрику) між матрицями парних порівнянь, яку будемо обчислювати за формулою

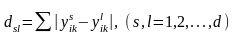. (7.11)

Смисл цього виразу полягає в тому, шо відстань між матрицями парних порівнянь визначається числом незбіжностей всіх значень елементів матриць (метрика Хемінга).

Використовуючи цю метрику, визначимо узагальнене ранжування як таку матрицю парних порівнянь, яка найкраще узгоджується з матрицями парних порівнянь ранжувань експертів. Поняття найкращого узгодження на практиці найчастіше визначають як медіану.

Медіана – це така матриця порівнянь, для якої сума відстаней до всіх матриць парних порівнянь мінімальна:

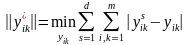. (7.12)

Покажемо, що побудова матриці парних порівнянь, яка відповідає медіані, здійснюється за принципом простої більшості голосів експертів для кожного елемента матриці. Модуль різниці змінних у (7.12) дорівнює або одиниці, або нулю, тому він дорівнює квадрату цієї різниці. Отже, замість (7.12) можна записати

. (7.13)

Піднесемо члени в круглих дужках до квадрата і, враховуючи, що квадрат змінної дорівнює самій змінній, одержуємо з (7.13)

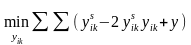. (7.14)

Підсумуємо спочатку за індексом s і, ввівши позначення

, (7.15)

одержимо з (7.14)

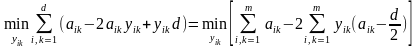. (7.16)

Перша сума в квадратних дужках постійна і не залежить від змінної 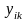. Тому мінімуму виразу в квадратних дужках відповідає максимум другого виразу, що записаний у круглих дужках. Отже,

. (7.17)

Максимум за змінними , які можуть приймати значення 0,1, досягається, якщо їх вибрати за таким правилом:

(7.18)

де d – кількість експертів.

Величини відповідно до (7.15) визначають кількість голосів, відданих експертами за перевагу i-го об’єкта над k-им об’єктом. Тому в узагальненій матриці парних порівнянь відповідно до оптимальних правил рішень (7.17) в ik-му елементі ставиться одиниця, тобто приймається, що , якщо більше половини експертів висловились за цю перевагу. Таким чином, усі елементи узагальненої матриці парних порівнянь визначаються за правилом більшості голосів.

У розглянутому алгоритмі побудови узагальненої матриці парних порівнянь можна врахувати компетентність експертів шляхом уведення коефіцієнтів компетентності у співвідношення (7.12):

. (7.19)

Виконуючи перетворення, аналогічні до співвідношень (7.13) – (7.18), одержуємо для випадку врахування коефіцієнтів компетентності експертів таке правило побудови узагальненої матриці парних порівнянь:

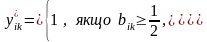(7.20)

де величини дорівнюють

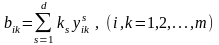. (7.21)

Величина порогу в (7.20) стала рівною внаслідок того, що величини можна розглядати як імовірність того, що i-й об’єкт має перевагу над k-м об’єктом.

За наявності декількох ситуацій експерти впорядковують об’єкти (рішення) для кожної ситуації окремо. Якщо відомі ймовірності ситуацій , де n – кількість ситуацій, то можна побудувати узагальнене ранжування, усереднене за всіма ситуаціями. Введемо для елементів матриць парних порівнянь ще один індекс j – номер ситуацій 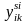. У цьому випадку узагальнена матриця парних порівнянь буде визначатися з умови

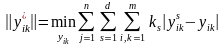. (7.22)

Виконуючи перетворення, аналогічні попереднім, одержимо таке правило побудови узагальненої матриці парних порівнянь, усереднених за допомогою ймовірностей усіх ситуацій:

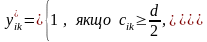(7.23)

де величини рівні

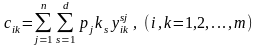. (7.24)

Зокрема, у випадку однакової компетентності експертів величини обчислюються за формулою

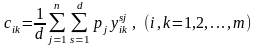. (7.25)

Правило побудови узагальненої матриці парних порівнянь (7.23) є найбільш загальним і включає, як окремий випадок, правила (7.18), (7.20).

Правило (7.23) визначає групову оцінку парних порівнянь. Для одержання узагальненої матриці парних порівнянь на основі матриці парних порівнянь застосовується послідовне виділення недомінованих об’єктів. Для послідовного виділення недомінованих об’єктів виконується операція транзитивного замикання матриці парних порівнянь і ранжування об’єктів за цією матрицею на основі підрахунку кількості одиниць у кожному стовпці матриці. Об’єкт, який має у своєму стовпчику найменше число одиниць, одержує перший ранг, другий ранг одержує об’єкт, який має в своєму стовпчику більше одиниць, ніж перший об’єкт, але менше всіх інших об’єктів і т.д.

Операція транзитивного замикання полягає у послідовному множенні матриці парних порівнянь саму на себе до тих пір, поки одержаний добуток не буде відрізнятися від попереднього кроку множення.

Слід відзначити, що якщо початкова інформація експертів про оцінку об’єктів надається у вигляді матриці парних порівнянь, то можливі випадки порушення умови транзитивності. Це зумовлено тим, що експерт здійснює порівняння тільки для пар об’єктів, а умова транзитивності зв’язана з розглядом не менше ніж трьох об’єктів. Порушення умови транзитивності в деяких матрицях парних порівнянь практично усувається обчисленням за формулою (7.15). Усереднення результатів за всією множиною експертів нівелює індивідуальні помилки експертів, в результаті чого окремі нетранзитивності об’єктів усуваються.

Приклад 1. Три експерти Е_і (і=1,2,3; d=3) оцінили значення двох заходів М_і (і=1,2; m=2) для рішення однієї проблеми (l=1) і дали нормовані оцінки заходів (табл.7.2)

Таблиця 7.2

	Е1	Е2	Е3
М1	0,3	0,5	0,2
М2	0,7	0,5	0,8

Проведемо обчислення групових оцінок заходів і коефіцієнтів компетентності експертів за формулами (7.4), (7.5), (7.6). Середні оцінки об’єктів першого наближення за формулою (7.7) при t=1 дорівнюють

Обчислимо величину 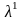за формулою (7.8). В результаті одержимо

.

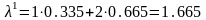Обчислюємо коефіцієнти компетентності першого наближення за формулою (7.9):

Обчислюючи групові оцінки об’єктів другого наближення, одержуємо вектор 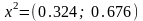. Вектор коефіцієнтів компетентності другого наближення дорівнює . Для третього наближення одержимо . Як випливає із третього наближення, вектор коефіцієнтів компетентності стабілізувався. Тому подальші обчислення не дадуть істотного уточнення.

Приклад 2. В результаті проведення ранжування чотирьох об’єктів п’ятьма експертами одержано впорядкування об’єктів, представлене в таблиці 7.3:

Таблиця 7.3

	О1	О2	О3	О4
Е1	2	1	4	3
Е2	3	2	4	1
Е3	1	2	3	4
Е4	3	1	2	4
Е5	1	2	4	3

На основі цієї таблиці складається для кожного експерта матриця парних порівнянь об’єктів. Ці матриці представлені в табл.7.4 – 7.8.

Таблиця 7.4 Таблиця 7.5

	О1	О2	О3	О4			О1	О2	О3	О4
О1	1	0	1	1		О1	1	0	1	0
О2	1	1	1	1		О2	1	1	1	0
О3	0	0	1	0		О3	0	0	1	0
О4	0	0	1	1		О4	1	1	1	1

Таблиця 7.6 Таблиця 7.7

	О1	О2	О3	О4			О1	О2	О3	О4
О1	1	1	1	1		О1	1	0	0	1
О2	0	1	1	1		О2	1	1	1	1
О3	0	0	1	1		О3	1	0	1	1
О4	0	0	0	1		О4	0	0	0	1

Таблиця 7.8 Таблиця 7.9

	О1	О2	О3	О4			О1	О2	О3	О4
О1	1	1	1	1		О1	5	2	4	4
О2	0	1	1	1		О2	3	5	5	4
О3	0	0	1	0		О3	1	0	5	2
О4	0	0	1	1		О4	1	1	3	5

Таблиця 7.10 Таблиця 7.11

	О1	О2	О3	О4			О1	О2	О3	О4
О1	1	0	1	1		О1	1	0	1	1
О2	1	1	1	1		О2	1	1	1	1
О3	0	0	1	0		О3	0	0	1	0
О4	0	0	1	1		О4	0	0	1	1

У матриці, зображеній в табл.7.9, знайдена сума матриць 7.4 –7.8 відповідно до формули (7.15) обчислення величин . За правилом (7.18) при умові, що число експертів , одержуємо порогове значення 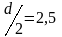і порівнюємо всі елементи в останній матриці (табл.7.9) з порогом 2,5. Якщо , то в узагальненій матриці парних порівнянь ставим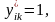о якщо 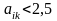, то ставимо 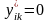. Результати порівняння елементів матриці з порогом 2,5 представлені в узагальненій матриці парних порівнянь (табл.7.10).

Для побудови узагальненого ранжування об’єктів виконуємо операцію транзитивного замикання шляхом множення одержаної узагальненої матриці парних порівнянь 7.10 на себе. Виконуючи це множення з урахуванням правил додавання і множення нульових змінних: 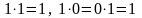, , одержимо табл.7.11.

Порівняння таблиць 7.10 і 7.11 показує, що вони однакові, тому попередня матриця вже є транзитивним замиканням. Найменша кількість одиниць розташована в другому стовпчику матриці, тому другий об’єкт одержує перший ранг. Другий ранг отримує перший об’єкт, третій ранг – четвертий і, нарешті, останній, четвертий ранг одержує третій об’єкт. Отже, узагальнене впорядкування чотирьох об’єктів, найбільш узгоджене з висновками п’яти експертів, має вигляд .