
Вариант 9
Задача 1. Трое гостей повесили в коридоре три свои шляпы. Внезапно погас свет, и гости надели шляпы наугад. Найти вероятности событий:
а) все трое возьмут свои шляпы; б) только уходящий первым возьмет свою шляпу; в) хотя бы один гость возьмет свою шляпу;
г) никто не возьмет свою.
Задача 2. В группе 5 отличников, 10 хорошо успевающих и 5 слабо успевающих студентов. Отличник сдает экзамен на "5" с вероятностью 0,9 и на "4" с вероятностью 0,1. Хорошо успевающий получает "5", "4" и "3" с вероятностями 0,3, 0,6 и 0,1, а слабоуспевающий получает "4", "3" и "2" с вероятностями 0,1, 0,5 и 0,4. Найти вероятность того, что наугад выбранный студент получит оценку не ниже "4".
Задача 3. Дана плотность распределения р(х) непрерывной случайной величины . Найти: а) параметр с; б) математическое ожидание М;
в) дисперсию D; среднеквадратическое отклонение ;
г) функцию распределения F(х); построить ее график;
д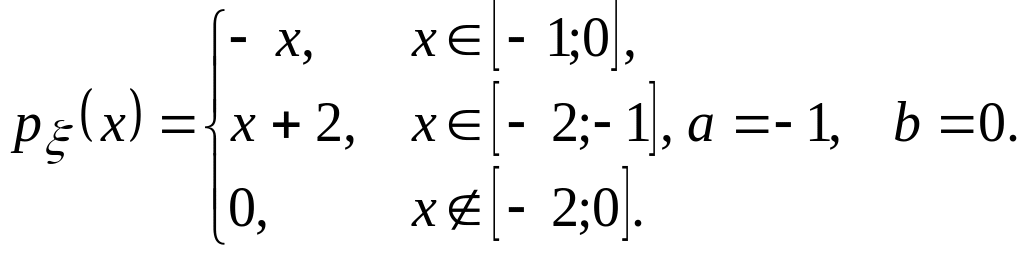 )
вероятность попадания
в промежуток [a; b) P{a
< b}.
)
вероятность попадания
в промежуток [a; b) P{a
< b}.
Задача 4. Известно математическое ожидание с.в. , имеющей распределение Пуассона. Найти закон распределения; найти D; найти P{k1 k2}. Ответить, какое событие более вероятно: k1 или < k1.
М = 4, k1 = 2, k2 = 5.
Задача 5. Для схемы Бернулли (n – число испытаний, р – вероятность успеха в одном испытании) определить вероятность осуществления события {k1<k<k2}, где k – количество успехов, пользуясь теоремой Муавра – Лапласа: n = 100, p = 1/5, k1 = 16, k2 = 32.
Задача 6. Система случайных величин (; ) имеет совместную плотность f(x;y). Найти с, плотности f(x), f(y) и коэффициент корреляции.
![]()
Задача 7. По результатам наблюдений случайной величины составлен дискретный вариационный ряд (xi – элементы выборки, ni – частоты).
1. Найти объем выборки и ее размах.
2.Составить интервальный вариационный ряд.
3. Построить гистограмму и эмпирическую функцию распределения.
4. Найти точечные оценки медианы, математического ожидания и дисперсии (смещенную и несмещенную).
5. Считая, что генеральная совокупность распределена по нормальному закону, найти доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью 1 - .
6. С помощью критерия 2 проверить при уровне значимости 1 гипотезу про нормальное распределение генеральной совокупности.
xi |
9,4 |
9,8 |
10 |
10,6 |
11 |
11,4 |
12 |
12,4 |
= 0,2 |
ni |
3 |
5 |
5 |
6 |
6 |
6 |
4 |
1 |
1 = 0,01 |
Вариант 10
Задача 1. В ящике 5 белых и 4 черных шаров. Наугад взяли 3 шара. Найти вероятность того, что среди них не больше двух белых.
Задача 2. Изделия удовлетворяют стандарту с вероятностью 0,96. Несовершенная система контроля с вероятностью 0,02 может забраковать стандартное изделие и с вероятностью 0,05 – наоборот, пропустить некачественное. Какова вероятность того, что изделия, прошедшее контроль, на самом деле стандартное?
Задача 3. Дана плотность распределения р(х) непрерывной случайной величины . Найти: а) параметр с;
б) математическое ожидание М;
в) дисперсию D; среднеквадратическое отклонение ;
г) функцию распределения F(х); построить ее график;
д) вероятность попадания в промежуток [a; b) P{a < b}.
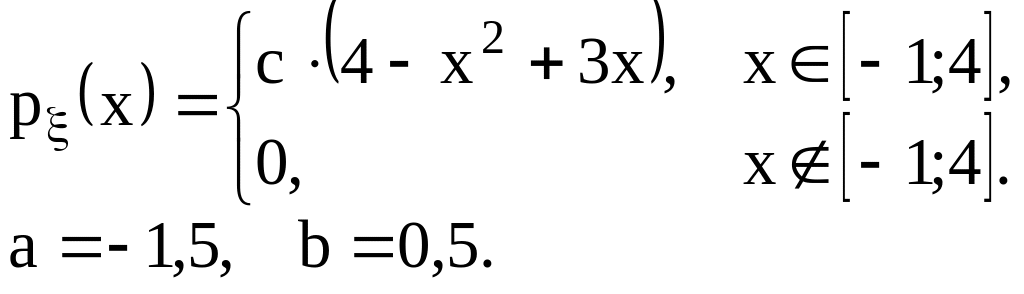
Задача 4. Известно математическое ожидание с.в. , имеющей распределение Пуассона. Найти закон распределения; найти D; найти P{k1 k2}. Ответить, какое событие более вероятно: k1 или < k1.
М = 1, k1 = 1, k2 = 4.
Задача 5. Для схемы Бернулли (n – число испытаний, р – вероятность успеха в одном испытании) определить вероятность осуществления события {k1<k<k2}, где k – количество успехов, пользуясь теоремой Муавра – Лапласа:
n = 100, p = 4/5, k1 = 82, k2 = 90.
Задача 6. Система случайных величин (; ) имеет совместную плотность f(x;y). Найти с, плотности f(x), f(y) и коэффициент корреляции.
![]()
Задача 7. По результатам наблюдений случайной величины составлен дискретный вариационный ряд (xi – элементы выборки, ni – частоты).
1. Найти объем выборки и ее размах.
2.Составить интервальный вариационный ряд.
3. Построить гистограмму и эмпирическую функцию распределения.
4. Найти точечные оценки медианы, математического ожидания и дисперсии (смещенную и несмещенную).
5. Считая, что генеральная совокупность распределена по нормальному закону, найти доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью 1 - .
6. С помощью критерия 2 проверить при уровне значимости 1 гипотезу про нормальное распределение генеральной совокупности.
xi |
8,4 |
8,6 |
9 |
9,2 |
9,4 |
9,8 |
10 |
10,4 |
= 0,05 |
ni |
2 |
2 |
3 |
7 |
5 |
4 |
3 |
2 |
1 = 0,05 |
